Levi-Civita paralelkenarımsı

Levi-Civita paralelimsi

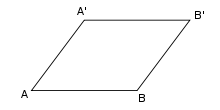
Diferansiyel geometrinin matematiksel alanı içinde, Levi-Civita paralelkenarımsı bir eğri uzay içinde bir dörtlüyanal Öklidyen düzlem içinde onun bir paralelkenar genelleme inşasıdır. Bu isim araştırmacı Tullio Levi-Civitaya ithafendir. Bir paralelkenar gibi, bir paralelkenarımsının iki zıt yüzleri AA′ ve BB′ paralel (paralel taşınım yoluyla) düz (bir jeodezik) olmasına rağmen, ancak dördüncü kenar A′B′ değil, genel olarak, paralel ya da AB kenarı boyunca aynı uzunlukta olacaktır.

Yapımı

Bir paralelkenar Öklidyen geometri içinde aşağıda inşa edilmiştir:

• Bir düz doğru parçası AB ve diğer düz doğru parçası AA′ ile başlayalım.
• AB sabit olan açı ile korunur ve A, A′ noktaları olarak aynı düzlem içinde kalıyor, uç nokta B 'ye AB boyunca AA′ parçasını kaydırın,ve B.
• B′ son parçanın son nokta etiketi ile böylece bu parça BB′dir.
• Çizilen bir A′B′ doğru parçasıdır.

Bir eğri uzay içinde, böylece bir Riemannian manifold veya daha genel herhangi manifold donanımı ile bir afin bağlantı, bu bir geodezikin "doğru parçaları" genellemesi ifadesidir. Bir uygun yakınkomşuluğu(böylece bir normal koordinat sistem içinde birtop) içinde, herhangi iki noktalar bir geodezik ile katılabilir. paralel taşımanın daha genel ifadesine diğer verilen yol bir doğru parçası boyunca kaymanın fikridir. Böylece, varsayalım ya bu manifold tamdır, veya bu yapı bir uygun yakınkomşuluk içinde yer alıyor, bir Levi-Civita parallelkenar türetimine ilk adımdır:

• bir geodezik AB ve diğer geodezik AA′ ile başlayalım. Burada geodezikler bir Riemannian manifold'un durumu içinde yay ile ölçeklendirmeye varsayım olur, veya bir afin bağlantının genel durumu içinde taşımaya afin ölçünün bir seçimi.
• A dan Bye AA′nın tanjant vektörü (paralel taşınım) "kayma".
• üstel gönderme yoluyla üretilen bir jeodezik Bde tanjant vektörle sonuçlanır. B′ ile bu geodeziğin son noktası etiketlendi, ve BB′ kendisi jeodeziktir.
• A′ ve B′noktasının bağlantıları A′B′ ile jeodeziktir.

Bir paralel arasındaki farkı nicel değerlendirmesi

Bu son geodezik yapım bağlantının uzunluğu A′B′ noktaları geriye kalan AB tabanının uzunluğundan farklı olarak genel içinde olasıdır. Bu fark Riemann eğrilik tensörü ile ölçülür. Hassas bir ilişkiyi belirtmek için, diyelimki AA′ bir tanjant vektör X ın A da üsteli olsun, ve A da Y nin üstel bir tanjant vektörün üsteli AB ise

${\displaystyle |A'B'|^{2}=|AB|^{2}+{\frac {8}{3}}\langle R(X,Y)X,Y\rangle +{\text{yüksek dereceli terimler}}}$

burada paralel kenarın, kenarlarının uzunluğu içinde daha yüksek derecenin koşulları ile baskılanmıştır.

Ayrık yaklaşıklık

Schild'in merdiveninin iki basamak.A₁X₁ ve A₂X₂ parçaları are A₀X₀ 'ın paralel taşınımının ilk sırasına bir yaklaşıklıktır eğri boyunca.

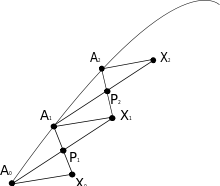
Parallel taşınım Schild'in merdiveni ile ayrıklanarak yakınsanabilir,bu yaklaşık paralelkenar ile Levi-Civita paralelkenarımsı yaklaşıklığıdır

Kaynakça

• Cartan, Élie (1983), Geometry of Riemannian Spaces, Math Sci Press, Massachusetts