Pi sayısı

Çapı 1 birim olan dairenin çevresi "π"ye eşittir.

Pi sembolü

Bu maddenin veya maddenin bir bölümünün gelişebilmesi için konuda uzman kişilere gereksinim duyulmaktadır. Ayrıntılar için maddenin tartışma sayfasına lütfen bakınız. Konu hakkında uzman birini bulmaya yardımcı olarak ya da maddeye gerekli bilgileri ekleyerek Vikipedi'ye katkıda bulunabilirsiniz.

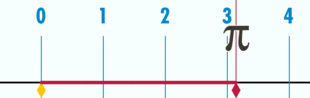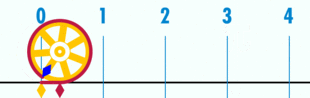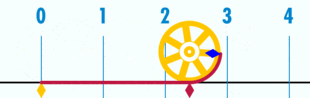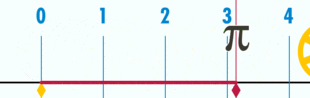
Pi sayısı ($\pi$), bir dairenin çevresinin çapına bölümü ile elde edilen irrasyonel matematik sabiti. İsmini, Yunanca περίμετρον (çevre) sözcüğünün ilk harfi olan π den alır. Pi sayısı, Arşimet sabiti ve Ludolph sayısı olarak da bilinir.^[1]

Tarihi

Fabrice Bellard, 2010 yılında Chudnovsky algoritması kullanarak sayının ilk 2.699.999.990.000 basamağını bulmuştur. Arşimet, 3 tam 1/7 ile 3 tam 10/71 arasında bir sayı olarak hesapladı. Mısırlılar 3,1605, Babilliler 3.1/8, Batlamyus 3,14166 olarak kullandı. İtalyan Lazzarini 3,1415926, Fibonacci ise 3.141818 ile işlem yapıyordu.

Yaklaşık değeri

Pi sayısının bazı yaklaşık değerleri şu şekildedir:

• Bölümler: 227, 333106, 355113, 5216316604, 10399333102, ve 24585092278256779.* ^[2]
• Onluk sayı sistemi : İlk yüz basamak; 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 ....^[3]
• İkilik sayı sistemi: 11.001001000011111101101010100010001000010110100011 ....
• On altılık sayı sistemi:3.243F6A8885A308D31319 ....^[4]
• Altmışlık sayı sistemi: 3;8,29,44,1

Pi ($\pi$) formülleri

Pi(π) formüllerinden başlıcaları şunlardır. ^[5]

Nilakantha Somayaji:

$\pi={3}+{\frac{4}{{3^{3}}-3}}-{\frac{4}{{5^{3}}-5}}+{\frac{4}{{7^{3}}-7}}-{\frac{4}{{9^{3}}-9}}+...$

$\pi={3}+{\frac{4}{2\times3\times4}}-{\frac{4}{4\times5\times6}}+{\frac{4}{6\times7\times8}}-{\frac{4}{8\times9\times10}}+...$

---

Franciscus Vieta:

$\pi=2\times\frac{2}{\sqrt{2}}\times\frac{2}{\sqrt{2+\sqrt{2}}}\times\frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}}\times\frac{2}{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}\times\cdots$

---

Gregory–Leibniz:

$\pi=4\sum_{n=0}^{\infty}\cfrac{(-1)^n}{2n+1}=4\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+-\cdots\right)\!=\cfrac{4}{1+\cfrac{1^2}{2+\cfrac{3^2}{2+\cfrac{5^2}{2+\ddots}}}}\!$

---

Isaac Newton:

$\pi=\sum_{n=0}^{\infty}\cfrac{{{2^{n+1}}\cdot{(n!)^2}}}{(2n + 1)!}$

---

Leonhard Euler:

$\pi=-iln(-1)$

---

Bailey-Borwein-Plouffe:

$\pi=\sum_{n=0}^{\infty}\biggl(\frac{1}{16}\biggr)^n\left(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}\right)$

---

Fabrice Bellard:

$\pi=\sum_{n=0}^\infty\frac{1}{2^6}\biggl(\frac{-1}{2^{10}}\biggr)^n\left(-\frac{2^5}{4n+1}-\frac{1}{4n+3}+\frac{2^8}{10n+1}-\frac{2^6}{10n+3}-\frac{2^2}{10n+5}-\frac{2^2}{10n+7}+\frac{1}{10n+9}\right)\!$

---

Adamchik-Wagon:

$\pi=\sum_{n = 0}^{\infty}\biggl(\frac{-1}{4}\biggr)^n\left(\frac{2}{4n+1}+\frac{2}{4n+2}+\frac{1}{4n+3}\right)$

Ayrıca bakınız

• Geometri
• Pi Günü

Kaynakça

1. Pi Sayısı
2. Eymard, Pierre; Lafon, Jean Pierre (1999). The Number Pi. American Mathematical Society. ISBN 978-0-8218-3246-2. 
3. Arndt & Haenel 2006, s. 240
4. Arndt & Haenel 2006, s. 242
5. Pi İngilizce Wikipedia Pi Sayfası

Dış bağlantılar

• Pi Çılgınlığı (Türkçe)
• Pi-Different (İngilizce)
• Project Gutenberg'de π'nin detaylı değeri (İngilizce)
• Pi formülleri ve online pi hesabı (İngilizce)