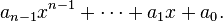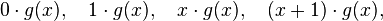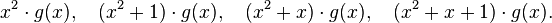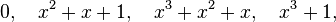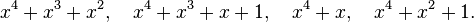Polinom kod

Kodlama kuramında polinom kod, bir doğrusal kod türüdür.

Tanım

Sabit bir 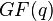$GF(q)$ sonlu alanındaki ögelere sembol denir. Polinom kod elde edilmesindeki amaç, 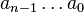$a_{n-1}\ldots a_0$ sembollerinden oluşan bir 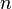$n$ dizisinin polinomu şöyledir:

$a_{n-1}x^{n-1} + \cdots + a_1x + a_0.\,$

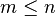$m \leq n$ sabit tam sayılar ve 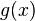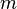$g(x)$, $m$ dereceden sabit polinom olsun. Buna üreteç polinom denir. 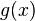$g(x)$ ile üretilen polinom kod, sözcükleri 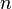$n$ den daha küçük dereceli polinom olan ve 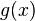$g(x)$ tarafından kalansız bölünebilir koddur.

Örnek

GF(2) alanında 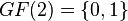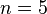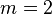$GF(2)=\{0,1\}$, $n=5$, $m=2$ ve üreteç polinomu 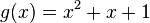$g(x)=x^2+x+1$ olsun. Bu kod aşağıdaki kod sözcüklerinden oluşur:

$0\cdot g(x),\quad 1\cdot g(x),\quad x\cdot g(x), \quad (x+1) \cdot g(x),$

$x^2 \cdot g(x),\quad (x^2+1)\cdot g(x),\quad (x^2+x)\cdot g(x), \quad (x^2+x+1) \cdot g(x).$

veya açıkça şöyle yazılır:

$0,\quad x^2+x+1,\quad x^3+x^2+x,\quad x^3+1,$

$x^4+x^3+x^2,\quad x^4+x^3+x+1,\quad x^4+x,\quad x^4+x^2+1.$

Bu ifadenin ikili sayı sistemindeki eşdeğeri şöyledir:

$00000,\quad 00111,\quad 01110,\quad 01001,$

$11100,\quad 11011,\quad 10010,\quad 10101.$

Burada her polinom kodun, gerçekte bir doğrusal kod olduğuna dikkat edin. Yani kod sözcüğünün doğrusal kombinasyonları yine kod sözcüğüdür. Böyle bir durumda alan GF(2) olur. Doğrusal kombinasyonlar ikili sayı sisteminde XOR ile elde edilir. Örneğin; 00111 XOR 10010 = 10101.