Schwarzschild metriği

Einstein'ın genel görelelik teorisine göre Schwarzschild metriği (Schwarzschild vakumu veya Schwarzschild çözümü olarak da bilinir) Einstein'ın alan denklemlerinin çözümüyle ortaya çıkmıştır. Küresel bir kütlenin dışındaki elektik yükü, angular momentumu ve evrensel kozmolojik sabiti sıfır varsayılan yerçekimsel alanı tarif eder. Bu çözüm yıldızlar veya gezegenler gibi düşük hızlarda dönen cisimler için oldukça yararlıdır. Dünya ve Güneş de bu cisimlere örnek olarak verilebilir. Bu çözüm ismini çözümünü 1916 yılında yayınlayan Karl Schwarzschild'den almıştır.

Birkhoff's theorem'ine göre, Schwarzschild metriği genellikle Eistein'ın alan denklemlerinin küresel simetrik, vakum çözümüdür. Schwarzschild kara deliği or statik kara delik yükü veya açısal momentumu yoktur. Schwarzschild kara deliği, Schwarzschild metriği tarafından tarif edilir ve diğer Schwarzschild kara deliğinden ayrılamaz kütlesi dışında.

Schwarzschild kara deliği küresel bir yüzey olarak şekillendirilebilir. Bir çevredeki küresel yüzey, genellikle, Schwarzschild yarıçapı yer almaktadır ve olay ufku denen bir kara deliğin yarıçapı olarak adlandırılır. Dönmeyen ve yüklü olmayan kütle tarafından oluşturulmuş kara delik için Schwarzschild yarıçapı daha küçüktür. Einstein alan denklemlerinin çözümü prensipte böylece koşullarının oluşumuna izin verecek kadar olumlu hale gelerek M kütleli obje için bu halde anca Schwarzschild kara deliği olabileceğini söyler (genel görelilik kuramına göre).

Schwarzschild metriği

Schwarzschild kordinatlarında, Schwarzschild metriği için çizgi elementi şu forma sahiptir:

${\displaystyle c^{2}{d\tau }^{2}=\left(1-{\frac {r_{s}}{r}}\right)c^{2}dt^{2}-\left(1-{\frac {r_{s}}{r}}\right)^{-1}dr^{2}-r^{2}\left(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}\right),}$

Bu denklemde

• ${\displaystyle \tau }$, uygun zaman (test paçacığıyla beraber aynı dünya çizgisinde ilerleyen saat tarafından ölçülen)
• c, ışık hızı,
• t, zaman kordinatı (çok ağır bir cisimden uzakta sonsuzdaki sabit bir saat tarafından ölçülmüş),
• ${\displaystyle r}$, radyal kordinat (ağır bir cismin küresel merkezi çevresindeki çemberin çevresinin 2π'ye bölünmesi olarak ölçülen)
• θ, enlemin tamamlayan açısı (radyan cinsinden, kuzeyle arasındaki açı)
• φ, boylam (radyan cinsinden)
• ${\displaystyle r_{s}}$, çok ağır bir cismin Schwarzschild yarıçapı, r_s = 2GM/c² denkleminden kütlesi M ile alakalı olan ölçek faktörü , G'nin yerçekimi sabitiolduğu durumda.^[1]

Klasik Newton teorisinde bu çözümün eş benzeri, noktasal cismin çevresindeki yerçekimi alanına denk gelmektedir.^[2]

Pratikte, r_s/r oranı neredeyse her zaman çok küçüktür. Mesela, Dünya'nın Schwarzschild yarıçapı r_s kabaca 8,7 millimeter (0.34 in) iken Güneş 3.3×10⁵ kat büyük ^[3] Schwarzschild yarıçapına sahiptir (yaklaşık olarak 3 km (1.9 mi)). Dünya'nın yüzeyinde bile, Newton yerçekimine ait düzeltmeler milyarda birdir. Bu oran sadece kara deliklerin ve nötronyıldızları gibi diğer çok ağır objelerin yanında kayda değer bir büyüklüğe erişir.

Schwarzschild metriği Einstein alan denklemlerininboş uzaydaki çözümüdür. Bunun anlamı sadece yerçekimi oluşturan bir objenin dışında geçerlidir. Bu R yarıçaplı küresel cismin r > R için geçerli çözümüdür. Yerçekimi oluşturan objenin hem içindeki hem dışındaki yerçekimi alanını tarif etmek için Schwarzschild çözümü r = R deki çözümlerle eşleştirilmelidir.

Tarihçe

Schwarzschild çözümü adını tam çözümü 1915 yılında bulan ve 1916 yılında yayımlayan Karl Schwarzschild'dan almıştır.^[4] Bu süre Einstein'ın genel görelelik teorisini yayımladıktan bir aydan bir süre sonrasına denk gelmektedir. Bu Einstein alan denklemlerinin ilk kesin sonucuydu diğer önemsiz düz uzay çözümlerinden farklıydı. Schwarzschild makalesi yayımlandıktan kısa bir süre sonra Birinci Dünya Savaşında, Almanya ordusunda görev alırken kaptığı hastalık sonucunda öldü.^[5]

Johannes Droste, 1916 yılında ^[6] yılında bağımsız olarak Schwarzschild çözümüyle aynı çözümü daha basit ve daha doğrudan bir yolla üretti.^[7]

Genel rölativitenin ilk yıllarında Schwarzschild'da ve Einstein alan denklemlerinde bulunan tekillik hakkında birçok karışıklık vardı. Schwarzschild orijinal makalesinde, kordinat sisteminin merkezine bizim şu an olay ufku dediğimiz şeyi koydu.^[8] Bu makalede ayrıca yardımcı değişken olarak şu an Schwarzschild radyal kordinatı olarak bildiğimiz şeyi tanıttı (üsteki denklemde r ). Schwarzschild denklemlerinde farklı radyal kordinatlar kullandı, Schwarzschild radyusunda sıfır olan.

Tekillik yapısının daha fazla tamamlanmış analizi David Hilbert^[9] tarafından sonraki yıllarda ifade edildi. Bu hem r = 0 ve r = r_s için tekilliği içeriyordu. Yine de r = 0 da teikliiğin 'gerçek' fiziksel tekillik olduğuna dair kabul vardı. r = r_s daki tekillik ucu açık kaldı.^[10]

1921'de Paul Painlevé ve 1922'de Allvar Gullstrand birbirlerinden bağımsız olarak bir ölçüm , Einstein'ın denklemlerinin bizim şu an Schwarzschild metrik koordinat dönüşümü olarak bildiğimiz küresel simetrik çözüm, R = rs de bir tekillik olmadığı Gullstrand–Painlevékordinatları ürettiler. Fakat onlar, çözümleri yalnızca koordinat dönüşümleri ve aslında Einstein'ın teorisi yanlış olduğunu iddia etmek için kullanılan çözümlerini kabul etmediler. 1924'te, Arthur Eddington koordinat işlem hatası olan r = rs de tekillik gösteren fakat "he also seems to have been unaware of the significance of this discovery" ilk koordinat dönüşümünü (Eddington–Finkelstein kordinatları) üretti. Daha sonra 1932'de, Georges Lemaître aynı etkiye sahip farklı bir koordinat dönüşümü düzenledi (Lemaîtrekordinatları) ve r = rs de tekilliğin fiziksel olmadığını ilk tanıyan oldu. 1939 yılında Howard Robertson azalan Schwarzschild metriğinde serbest düşme gözlemcisi r = rs tekilliği ile uygun zamanın sınırlı bir miktarında t çaprazlandığını gösterdi.^[10]

1950 yılında, John Synge Schwarzschild metriğin maksimal analitik uzantısını gösteren, yeniden r = rs de tekilliğin bir koordinat işlem hatası olduğunu ve iki horizonla gösterildiğni gösteren bir makale yayınladı^[11]. Benzer bir sonuç, daha sonra Martin Kruskal^[12] tarafından yeniden keşfedildi. Onun koordinatları Synge'ninkilerden daha basitti fakat ikisi de tüm uzayzamanı kaplıyan koordinatların tek bir setini sağladılar. Ancak, belki de Lemaître ve Synge ve makaleleri kendi sonuçlarını yayınladı hangi dergilerin bilinmezlik fiziksel olarak Einstein Schwarzschild yarıçapı o tekillik inanarak dahil alanının önemli oyuncularından çoğu ile, fark edilmeden gitti^[10]

Diferansiyel geometrinin daha kesin araçları tekil olmak üzere bir Lorentz manifoldu için ne anlama geldiğini daha kesin tanımları sağlayan, genel görelilik alanına girdiğinde İlerleme sadece 1960 yılında yapılmıştır. Bu olay ufkunun (sadece bir yönde geçilebilir uzay bir hiperyüzeyin) olarak Schwarzschild metrik r = rs tekillik kesin tanımlanmasına yol açtı^[10]

Tekillikler ve kara delikler

Schwarzschild çözümü r= 0 and r = r_s da bazı tekilliklerivarmış gibi gözüküyordu; bozı metrik bileşenler bu uzaklıkta kayboluyordu. Schwarzschild metriğin sadece yerçekimi oluşturan obje için sadece R'den çok daha büyük değerlerde geçerli olmasından dolayı, R > r_s olduğu sürece bir problem yoktu. Sıradan yıldızlar ve gezegenler için bu her zaman böyle olurdu. Mesela Güneş'in yarıçapı yaklaşık olarak 700,000 km uzunluğundadır, Schwarzschild yarıçapı sadece 3 km iken.

r = r_s deki tekillik Schwarzschild kordinatlarını iki bağımsız plakaya böler. r > r_s uzunluğundaki dıştaki plaka yıldızların ve gezegenlerin yerçekimi alanıyla alakalıdır. < r < r_s daki iç plaka ise r = 0 da tekillik içerir ve r = r_s de dıştaki plakadan tekillik ile ayrılır. Schwarzschild kordinatları dolayısıyla iki plaka arasında fiziksel ilişki vermez. Bu yüzden belki de iki ayrı çözüm olarak incelenebilir. r = r_s deki tekillik aslında bir illüzyondur. kordinat tekilliğinin bir anıdır. İsmin ifade ettiği şekilde, tekillik kötü seçilmiş kordinatlardan veya kordinat koşullarından dolayı artar. Kordinat sistemini değiştirdiğimizde (mesela Lemaitre kordinatları, Eddington–Finkelstein kordinatları, Kruskal–Szekeres kordinatları, Novikov kordinatları, veya Gullstrand–Painlevé kordinatları) metric r = r_s de düzenli olur ve r_s nin r'den küçük değerlerine genişler. Farklı kordinat değişikliği kullanmak içteki ve dıştaki plakayı birbiri ile bağlayabilir.^[13]

r = 0 durumu farklıdır. Bir çözüm tüm r geçerli olmasını isterse bir kökeni, gerçek bir fiziksel tekillik, ya da yerçekimi tekillik geçmektedir. gerçek bir tekillik olduğunu görmek için bu koordinatların seçimi bağımsız miktarlarda bakmak gerekir. Böyle önemli miktarda tarafından verilen Kretschmann değişmez olduğunu gösterir.

${\displaystyle R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }={\frac {12{r_{s}}^{2}}{r^{6}}}={\frac {48G^{2}M^{2}}{c^{4}r^{6}}}\,.}$

r = 0 da eğrilik sonsuza gider, Bir tekillik varlığını gösteren . Bu noktada ölçüm ve uzay-zaman kendisi artık iyi tanımlanmıştır. Uzun bir süre için, bu tür bir çözelti, fiziksel olmayan olduğu düşünüldü . Ancak, genel görelilik daha büyük bir anlayışla bu tür tekillik teorisinin genel bir özelliği olmasına ve sadece egzotik özel durum olduğunda gerçekleşmesine yol açtı. Bu tür çözümler artık mevcut olduğuna inanılmaktadır ve kara delikler denir.

Alınan Schwarzschild çözümü , tüm r > 0 için geçerli olmak üzere , bir Schwarzschild kara delik denir . Bazı oldukça tuhaf özelliklere sahip olsa da , Einstein alan denklemlerinin mükemmel geçerli bir çözümdür . R < Schwarzschild radyal koordinat rs r zamansal olur ve süresi t spacelike olur koordinat . Sabit r A eğri artık bir parçacığın veya gözlemci olası dünyaçizgisinin değil, bir kuvvet vardır tutmak için denemek için sarf bile ; uzay-zaman neden ve etkisi ( parçacığın gelecekteki ışık konisi ) yönü tekillik [ kaynak belirtilmeli ] içine işaret o kadar kavisli olduğu için bu oluşur . Yüzey r = rs kara deliğin olay ufku denir demarcates . Bu ışık artık yerçekimi alanı kaçabilir noktası geçmiş temsil eder. Kimin yarıçapı R Herhangi bir fiziksel nesne bir kara delik yerçekimi çöküşü geçmesi ve olacak Schwarzschild yarıçapı daha az veya eşit olur^[14]

Alternatif kordinatlar

Schwarzschild çözümü yukarda kullanılan Schwarzschild kordinatları dışında birçok kordinat seçimiyle ifade edilebilir. Farklı seçimler çözümün farklı yönlerini vurgulamaktadır. Aşağıdaki tablo bazı popüler seçimleri göstermektedir.

Alternative coordinates

Kordinatlar	Çizgi elementi	Notlar	Özellikler
Eddington-Finkelstein kordinatları (içeri doğru)	${\displaystyle {\Big (}1-{\frac {r_{s}}{r}}{\Big )}dv^{2}-2dvdr-r^{2}d\Omega ^{2}}$		ufukta düzenli gelecek ufuklara genişliyor
Eddington-Finkelstein kordinatları (dışarı doğru)	${\displaystyle {\Big (}1-{\frac {r_{s}}{r}}{\Big )}du^{2}+2dudr-r^{2}d\Omega ^{2}}$		ufukta düzenli gelecek ufuklara genişliyor
Gullstrand–Painlevé kordinatları	${\displaystyle {\Big (}1-{\frac {r_{s}}{r}}{\Big )}dT^{2}-2{\sqrt {\frac {r_{s}}{r}}}dTdr-dr^{2}-r^{2}d\Omega ^{2}}$		ufukta düzenli
Isotropic kordinatlar	${\displaystyle {\frac {(1-{\frac {r_{s}}{4R}})^{2}}{(1+{\frac {r_{s}}{4R}})^{2}}}{dt}^{2}-{\Big (}1+{\frac {r_{s}}{4R}}{\Big )}^{4}(dx^{2}+dy^{2}+dz^{2})}$	${\displaystyle R={\sqrt {x^{2}+y^{2}+z^{2}}}}$[15]	sürekli zaman skalaları üzerine ışık konileri genişliyor
Kruskal-Szekeres kordinatları	${\displaystyle {\frac {4r_{s}^{3}}{r}}e^{-r/r_{s}}(dT^{2}-dR^{2})-r^{2}d\Omega ^{2},}$	${\displaystyle T^{2}-R^{2}={\Big (}1-{\frac {r}{r_{s}}}{\Big )}e^{r/r_{s}}}$	ufukta düzenli uzay zamana sonsuz olarak genişliyor
Lemaitre kordinatları	${\displaystyle dT^{2}-{\frac {r_{s}}{r}}dR^{2}-r^{2}d\Omega ^{2}}$	${\displaystyle r={\Big [}{\frac {3}{2}}(R-T){\Big ]}^{2/3}r_{s}^{1/3}}$	ufukta düzenli

YUkardaki tabloda bazı kısa sonuçlar gösterilmiştir. Işık hızı c bire yerleştirilmiştir. ${\displaystyle d\Omega ^{2}=d\theta ^{2}+\sin(\theta )^{2}d\phi ^{2}}$ formülü iki boyutlu yuvarlağın metriğinde kullanılırc. Dahası, her girdide R ve T, alternatif radyal ve zaman kordinatlarını delalet eder. Burada R ve/veya T'nin girdiden girdiğe değişiklik gösterdiği fark edilmelidir.

Flamm'ın paraboloidi

QuoteA Flamm en paraboloid arsa. Bu konudan bağımsız olan gravity well ile karıştırılmamalıdır.

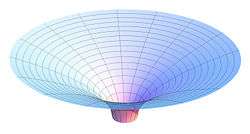
${\displaystyle r>r_{s}}$ için uzaysal eğrilik grafikte örüldüğü gibi canlandırılabilir. Sabit zaman da Schwarschild çözümü olan ekvatoral bir kesik olsun ( teta açısı π/2, zaman sabit) , parçacığın hareketli pozisyonu yine Schwarzschild koordinatları (r ve φ) olsun.Şimdi ek olarak Öklidsel boyut olsun buna w diyelim ki bu boyuttun aslında fiziksel bir gerçekliği yok (yani uzay zamanının bir parçası değil) .

${\displaystyle w=2{\sqrt {r_{s}\left(r-r_{s}\right)}}.}$

Sonra Flamm ın paraboloid ine göre düzlemi , çukurlu yüzeyle w yönünde (r, φ) ya bağlı olarak değiştirin

${\displaystyle dw^{2}+dr^{2}+r^{2}d\varphi ^{2}=-c^{2}d\tau ^{2}={\frac {dr^{2}}{1-{\frac {r_{s}}{r}}}}+r^{2}d\varphi ^{2}}$

Bunun sonucunda da, Flamm en paraboloit Schwarzschild metrik mekansal eğriliği görselleştirmek için yararlıdır. Bununla birlikte, iyi bir yerçekimi ile karıştırılmamalıdır. Bunun üzerine tüm mesafeleri (bu süre bir anda bir kesitidir, bu yüzden hareket herhangi bir parçacık sonsuz hızı olurdu) spacelike olduğundan sıradan (masif veya kütlesiz) parçacık, paraboloidin yatan bir dünyaçizgisinin olabilir. Hatta bir Takyon bir safça bir "lastik levha" benzetme beklediğiniz yol boyunca hareket olmaz: Özellikle, gamze merkezi kitle doğru yukarı yerine aşağı, Takyon yolunun hala eğrileri, değil uzakta işaret çizilmiş ise.

Flamm's paraboloidi aşağıdaki şekilde türetilebilir. silindirik kordinatlardaki (r, φ, w) Euclidean metriği şu şekilde yazılır:

${\displaystyle \mathrm {d} s^{2}=\mathrm {d} w^{2}+\mathrm {d} r^{2}+r^{2}\mathrm {d} \phi ^{2}.\,}$

Yüzeyi ${\displaystyle w=w(r)}$ fonsiyonu ile tarif edersek, Euclidean metriği şu şekilde yazılabilir

${\displaystyle \mathrm {d} s^{2}=\left[1+\left({\frac {\mathrm {d} w}{\mathrm {d} r}}\right)^{2}\right]\mathrm {d} r^{2}+r^{2}\mathrm {d} \phi ^{2},}$

Bunu ekvatoral düzlemde (θ = π/2) belirli bir zamanda (t = sabit, dt = 0) Schwarzschild metriği ile karşılaştırırsak

${\displaystyle \mathrm {d} s^{2}=\left(1-{\frac {r_{s}}{r}}\right)^{-1}\mathrm {d} r^{2}+r^{2}\mathrm {d} \phi ^{2},}$

w(r) için alan integralleri şu şekilde ifade edilir:

${\displaystyle w(r)=\int {\frac {\mathrm {d} r}{\sqrt {{\frac {r}{r_{s}}}-1}}}=2r_{s}{\sqrt {{\frac {r}{r_{s}}}-1}}+{\mbox{constant}}}$

Bu da Flamm's paraboloidine karşılık gelmektedir.

Yörünge hareketi

Schwarzschild metriğinde bir yörüngede hareket eden parçacık ${\displaystyle r>3r_{s}}$ için sabit bir yörüngeye sahip olabilir. ${\displaystyle 3r_{s}/2}$ ve ${\displaystyle 3r_{s}}$ değerleri arasındaki dairesel yörüngeler kararsızdır. ${\displaystyle r<3r_{s}/2}$ değeri içinse bir yörünge söz konusu değildir. minimum yarıçapı ${\displaystyle 3r_{s}/2}$ denk gelen yörüngeler için yörünge hızı ışık hızına yaklaşır. ${\displaystyle r}$ nin ${\displaystyle r_{s}}$ ve ${\displaystyle 3r_{s}/2}$ değerleri arasında sabit bir değer alması mümkündür ama bu sadece bir kuvvetin sürekli etki etmesiyle gerçekleşebilir.

Böyle Mercury'nin gibi dairesel olmayan yörüngeler, klasik beklenenden daha küçük yarıçapı daha uzun yaşamak. Bu daha dramatik bir durumda daha az aşırı versiyonu olan bir parçacık olay ufkunun içinden geçerken görülen ve sonsuza kadar onun içinde yaşıyor olabilir. Merkür'ün durumda ve olay ufkunun geçmiş düşen bir nesnenin durumunda arasındaki ara, uydu neredeyse dairesel yörüngelerde bir keyfi sayıda çalıştırmak için yapılabilir hangi "bıçak sırtı" yörüngeler, sonra gibi egzotik olasılıklar vardır hangi dışa geri uçar.

Simetriler

Schwarzschild metriğin izometri grupları kendisine zaman eksenini alan (yıldızın yörüngesi) on boyutlu Poincaré grubun alt kümesidir. Bu mekansal çeviriler (üç boyut) ve artırır (üç boyut) atlar. Zaman çeviriler (tek boyut) ve dönmeler (üç boyut) korur. Böylece dört boyutu vardır. Poincare grubu gibi, bu dört bağlı bileşeni vardır: kimlik bileşeni; Zaman bileşeni ters; uzaysal ters bileşen; ve zaman ters ve mekansal ters hem de bileşen.

Alıntılar

"Es ist immer angenehm, über strenge Lösungen einfacher Form zu verfügen." (Uğraşlarınız sonucunda kesin sonuçlarınızın basit bir halde olması her zaman daha iyidir) – Karl Schwarzschild, 1916.

1. Landau & Liftshitz 1975.
2. Ehlers, J. (1997). "Examples of Newtonian limits of relativistic spacetimes". Classical and Quantum Gravity 14: A119–A126. Bibcode 1997CQGra..14A.119E. DOI:10.1088/0264-9381/14/1A/010. 
3. Tennent, R.M., ed. (1971). Science Data Book. Oliver & Boyd. ISBN 0-05-002487-6. 
4. Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 7: 189–196. Bibcode 1916AbhKP......189S. http://www.archive.org/stream/sitzungsberichte1916deutsch#page/188/mode/2up.  For a translation, see Antoci, S.; Loinger, A. (1999). "On the gravitational field of a mass point according to Einstein's theory". arΧiv: physics/9905030 [physics]. 
5. O'Connor, John J.; Robertson, Edmund F., "Karl Schwarzschild", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Schwarzschild.html .
6. Droste, J. (1917). "The field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field". Proceedings of the Royal Netherlands Academy of Arts and Science 19 (1): 197–215. Bibcode 1917KNAB...19..197D. http://www.dwc.knaw.nl/DL/publications/PU00012325.pdf. 
7. Kox, A. J. (1992). "General Relativity in the Netherlands:1915-1920". Eisenstaedt, J.; Kox, A. J.. Studies in the History of General Relativity. Birkhäuser. s. 41. ISBN 978-0-8176-3479-7. http://books.google.nl/books?id=vDHCF_3vIhUC&lpg=PA39. 
8. Brown, K. (2011). Reflections On Relativity. Lulu.com. Chapter 8.7. ISBN 978-1-257-03302-7. http://mathpages.com/rr/s8-07/8-07.htm. 
9. Hilbert, David (1924). "Die Grundlagen der Physik". Mathematische Annalen (Springer-Verlag) 92 (1-2): 1-32. DOI:10.1007/BF01448427. 
10. Earman, J. (1999). "The Penrose–Hawking singularity theorems: History and Implications". Goenner, H.. The expanding worlds of general relativity. Birkhäuser. s. 236-. ISBN 978-0-8176-4060-6. http://books.google.com/books?id=5mGZno8CvnQC&pg=PA236. 
11. Synge, J. L. (1950). "The gravitational field of a particle". Proceedings of the Royal Irish Academy 53 (6): 83–114. 
12. Kruskal, M. D. (1960). "Maximal extension of Schwarzschild metric". Physical Review 119 (5): 1743–1745. Bibcode 1960PhRv..119.1743K. DOI:10.1103/PhysRev.119.1743. 
13. Hughston, L.P.; Tod, K.P. (1990). An introduction to general relativity. Cambridge University Press. Chapter 19. ISBN 978-0-521-33943-8. http://books.google.com/books?id=2q5Rdjn0qfgC&lpg=PA126. 
14. Brill, D. (2012). "Black Hole Horizons and How They Begin". Astronomical Review. http://astroreview.com/issue/2012/article/black-hole-horizons-and-how-they-begin. 
15. Eddington, A. S. (1924). The Mathematical Theory of Relativity (2nd bas.). Cambridge University Press. s. 93.