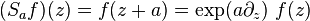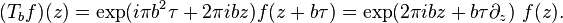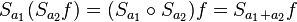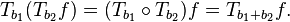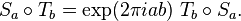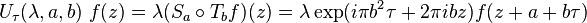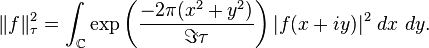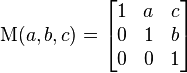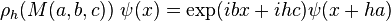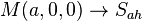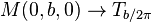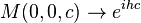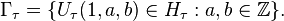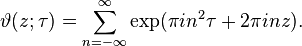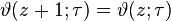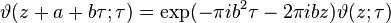Teta gösterim
matematik'te, teta gösterim kuantum mekaniği'ndeki Heisenberg grup'unun özel bir temsilidir . Bu aslında adını Jacobi teta fonksiyonu'ndan alır.Heisenberg grubunun hareket altındaki değişmezlik gösteren ayrık bir alt grubudur. Bu gösterimi popüler eden David Mumford oldu.
Yapım
Bu teta gösterimi sürekli Heisenberg grubunun 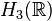 gerçek sayıların alanı üzerinde bir gösterimdir. Bu gösterim, bir özelHilbert uzayı grup ögesinin hareketidir. Aşağıdaki yapı önce Heisenberg grup üreteçlerine karşılık gelen işlemcileri tanımlayarak ilerler.Daha sonra bunu hareketin tanımlanmış olduğu Hilbert uzayı izomorfizm'inin tarafından kullanılan gösteriminin bir ifadesi izler
gerçek sayıların alanı üzerinde bir gösterimdir. Bu gösterim, bir özelHilbert uzayı grup ögesinin hareketidir. Aşağıdaki yapı önce Heisenberg grup üreteçlerine karşılık gelen işlemcileri tanımlayarak ilerler.Daha sonra bunu hareketin tanımlanmış olduğu Hilbert uzayı izomorfizm'inin tarafından kullanılan gösteriminin bir ifadesi izler
Grup üreteçleri
Diyelimki f(z) bir holomorfik fonksiyon olsun, diyelimki a ve b gerçel sayı'lar olsun, ve diyelimki 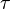 sabitlenebilir, ama keyfi karmaşık sayı üst yarı-düzlem içinde;böylece
sabitlenebilir, ama keyfi karmaşık sayı üst yarı-düzlem içinde;böylece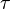 sanal kısmı pozitiftir. işlemcileri tanımlanan Sa ve Tb işlemcileri böylece holomorfik fonksiyonlar gibi davranırlar
sanal kısmı pozitiftir. işlemcileri tanımlanan Sa ve Tb işlemcileri böylece holomorfik fonksiyonlar gibi davranırlar
ve
Her işlemcinin bir tek-parametreli altgrup ürettiği görülebilir:
ve
Ancak, S ve T yer değiştiremez:
Böylece S ve T ile bir nilpotent Lie grup'unun bir birimsel faz formunu birlikte görebiliriz,yani (sürekli gerçel) Heisenberg grubu, parametrize edilmiş 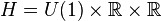 burada U(1) birimsel grup'tur.
burada U(1) birimsel grup'tur.
Bir genel grup ögesi 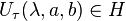 olarak sonra bir holomorfik f(z)üzerine etki eder.
olarak sonra bir holomorfik f(z)üzerine etki eder.
burada 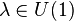 .
. 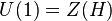 Hın merkez'idir ,değişmeli altgrup
Hın merkez'idir ,değişmeli altgrup ![[H, H]](../I/m/9d2dde778da1e98d5cd320522d9edae6.png) 'tır.
'tır.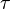 parametresi
parametresi 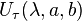 içerisinde
içerisinde 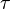 temsili her farklı bir değer grubunun eylem farklı bir farklı eyleme yol açtığını hatırlatmak için sadece hizmet vermektedir.
temsili her farklı bir değer grubunun eylem farklı bir farklı eyleme yol açtığını hatırlatmak için sadece hizmet vermektedir.
Hilbert uzayı
Grup ögelerinin hareketi 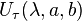 fonksiyonlar belirli bir Hilbert uzayında birimsel ve indirgenemezdir. τ sabit bir değeri için,karmaşık düzlemin bir normu olarak tanımlanan tam fonksiyonu
fonksiyonlar belirli bir Hilbert uzayında birimsel ve indirgenemezdir. τ sabit bir değeri için,karmaşık düzlemin bir normu olarak tanımlanan tam fonksiyonu
Burada,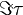
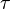 nin sanal kısımdır ve integrasyonun domeni tam karmaşık düzlemdir.Diyelimki
nin sanal kısımdır ve integrasyonun domeni tam karmaşık düzlemdir.Diyelimki 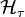 tam fonksiyonun kümesi olsun f ile sonlu normdur. Bu ifade
tam fonksiyonun kümesi olsun f ile sonlu normdur. Bu ifade 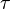 uzayı parametre seçimine bağlı göstermek için kullanılır
uzayı parametre seçimine bağlı göstermek için kullanılır 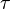 . Bu
. Bu 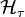 bir Hilbert uzayı formudur.
bir Hilbert uzayı formudur. 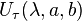 'ın hareketi yukarıda birimsel olarak verilen
'ın hareketi yukarıda birimsel olarak verilen 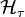 'tır, bu,
'tır, bu, 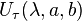 Bu alan üzerinde norm korunur. Sonuç olarak,
Bu alan üzerinde norm korunur. Sonuç olarak,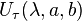 'ın hareketi olarak
'ın hareketi olarak 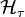 indirgenemeyen'dir.
indirgenemeyen'dir.
İzomorfizm
Heisenberg grubunun Yukarıda teta gösterimi standart Heisenberg grubunun Weyl gösterimi'ne izomorfiktir. Özel olarak, Bu şu demektir.
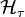 ve L2(R) are izomorfik oarak H-modül. Diyelimki
ve L2(R) are izomorfik oarak H-modül. Diyelimki
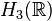 bir genel grup ögesi için durur.Standart Weyl temsili ile, Her reel sayı için h, burada bir
bir genel grup ögesi için durur.Standart Weyl temsili ile, Her reel sayı için h, burada bir
gösterim 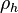 acting on L2(R) olarak
acting on L2(R) olarak
için 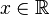 and
and 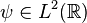 .
.
Burada, h Planck sabiti'dir. Bu gösterime belirsizlik birimi denir. Buna karşılık gelen teta temsilidir:
Ayrık altgruplar
Altgrubun tanımı 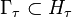 olarak
olarak
Jacobi teta fonksiyonu olarak tanımlanır.
z değişmez altında bu bir tam fonksiyon'dur 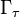 . Bu teta işlevinin özelliklerinin devamı:
. Bu teta işlevinin özelliklerinin devamı:
ve
ise aveb tamsayıdır. Bu Jacobi teta benzersiz bir işlevi olduğu gösterilebilir.
Kaynakça
- David Mumford, Tata Lectures on Theta I (1983), Birkhauser, Boston ISBN 3-7643-3109-7