Toplamaya göre ters

Matematikte, bir a sayısını toplamaya göre tersi, a ile toplamı 0 olan bir sayıdır. Bu işleme, işaret değiştirme veya negasyon denir. Reel sayı için ters işarettir: Pozitif sayının tersi negatif ve negatif sayının tersi pozitiftir. 0'nun toplamaya göre tersi kendisidir.

a nın toplamaya göre tersi, tekli eksi işareti ile şöyle ifade edilir: −a. Örneğin; 7'nin toplamaya göre tersi -7'dir. Çünkü 7 + (−7) = 0. −0,3 'ünkü 0,3'dür. Çünkü, −0,3 + 0,3 = 0 .

Toplamaya göre ters, toplamanın ikili işlemleri ile ters öge olarak tanımlanır. Bu da matematiksel nesneleri diğerlerinden ayırmanın bir genelleştirmedir. Herhangi bir ters işlem için, çift toplamaya göre ters, hiçbir etki yapmaz, şöyle ki: −(−x) = x.

Karmaşık sayılarda iki ⁸√1'in sekiz değerleri, birbirlerine terstir

Sıkça kullanılan örnekler

Herhangi bir halkadaki bir sayı için toplamaya göre tersi genellikle -1 ile çarpımıdır. Bu, −n = −1 × n . Örneğin tam sayılar, rasyonel sayılar ve karmaşık sayılar, sayılar halkasıdır.

Çıkarma ile ilişkisi

Toplamaya göre ters, çıkarma ile çok yakından ilişkilidir. ve toplamanın tersi olarak gösterilebilir, şöyle ki:

a − b  =  a + (−b).

Tam tersine toplamaya göre ters, sıfırdan çıkarma olarak düşünülebilir:

−a  =  0 − a.

Her ne kadar tipografide tek "−" den sonra boşluk olmazsa bile, tekli çıkarma işareti gösteriminde, "0" sembolü göz ardı edilecek gösterilebilir.

Diğer özellikler

Aşağıda, toplama işlemi ile birlikte, işaret değiştirmenin cebirsel özellikler listelenmiştir:

−(a + b) = (−a) + (−b)

a − (−b) = a + b

(−a) × b = a × (−b) = −(a × b)

(−a) × (−b) = a × b

özellikle, (−a)² = a²

Formal tanım

+ gösterimi, genellikle değişmeli ikili işlemleri için kullanılır. Örneğin; tüm x ve y için x + y = y + x'dir. Eğer o birim öge olursa, (tüm x için, 1=x + o ( = o + x ) = x ise), bu öge eşsizdir ( o′ = o′ + o = o ). x için , x′ oluyorsa, örneğin; x + x′ ( = x′ + x ) = o oluyorsa, x′ ne, x in toplamaya göre tersi denir.

Eğer +, birleşmeli ise, tüm x, y ve z için, (( x + y ) + z = x + ( y + z ) olur. Bunun toplamaya göre tersi eşsizdir.

x″ = x″ + o = x″ + (x + x′) = (x″ + x) + x′ = o + x′ = x′

Örneğin reel sayılar toplandığında, birleşmeli olur ve her bir reel sayının toplamaya göre tersi eşsizdir.

Diğer örnekler

Aşağıdaki örneklerin tümü abelian gruplarında karşımıza çıkar.

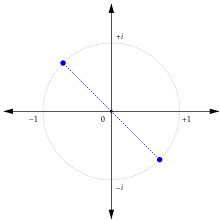
• karmaşık sayılar: −(a + bi)  =  (−a) + (−b)i. Karmaşık düzlemde bu işlem, bir karmaşık sayının orijin etrafında 180 derece dönmesidir.
• reel veya karmaşık değerli fonksiyonların toplamı: burada bir f fonksiyonunun toplamaya göre tersi, −f şöyle tanımlanır: tüm x için, (−f )(x) = − f (x) . Burada f + (−f ) = o , tüm x için, sıfır fonksiyonu: ( o(x) = 0 ).
• more generally, what precedes applies to all functions with values in an abelian group ('zero' meaning then the identity element of this group):
• diziler, matrislerde özel tür fonksiyonlardır.
• Vektör uzayında toplamaya göre ters, −v ile sembolize edilir ve v nin karşıt vektörü olarak adlandırılır. Asıl vektör ile aynı büyüklükte fakat zıt yönlüdür. Toplamaya göre ters, −1 ile skaler çarpmaya eşittir. Öklid uzayı için bu, orijine göre nokta yansımasıdır.
• Modüler aritmetikte, x in modüler toplamaya göre tersi şöyle tanımlanır: a + x ≡ 0 (mod n). Bu toplamaya göre ters daima vardır. Örneğin, 3'ün modül 11'e göre tersi, 8'dir. Çünkü bunu çözümü şöyledir: 3 + x ≡ 0 (mod 11).

Ayrıca bakınız

• Mutlak değer
• Çarpmaya göre ters