Zaman serisi

Zaman serisi: en uygun ve farklı düzleştirmelere sahip, rastgele veri artış eğilimi

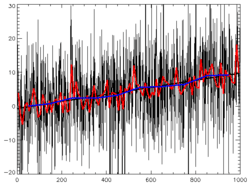
İstatistik, sinyal işleme, ekonometri ve matematiksel finansta bir zaman serisi veri noktalarının sıklığıdır ve düzenli zaman aralıklarında, ardışık zaman alanlarında tipik olarak ölçülür. Zaman serisine örnek olarak, İMKB endeksinin günlük kapanış değeri veya Türkiye'deki kızılırmak nehrinin yıllık akış hacmi (debisi) verilebilir. Zaman serisi analizi, anlamlı istatistikleri ve verinin diğer istatistiklerini almak için birkaç yöntemi vardır. Zaman serisi tahmini önceden bilinen olayları baz olarak gelecek olayları tahmin etmenin bir kavramsal modelidir. Ekonometride zaman serisi tahminine bir örnek, önceki başarımlarına (performanslarına) bakarak bir hisse senedinin açılış fiyatını öngörmektir.

Zaman serisi analizinin yöntemleri iki sınıfa ayrılabilir: frekans domeni ve zaman domeni yöntemleri. Önceden tayf analizini (spektrum analiz) içerirken son zamanlarda dalgacık analizini de kapsar.

Analiz

Farklı amaçlara uygun olan zaman serisinde kullanılabilir veri analizinin birkaç türü vardır.

Genel araştırma

• Veri serisinin grafiksel araştırması
• Seri bağımlılığa incelemek için otokorelasyon analizi
• Mevsimsellikle ilişkili olması gerekmeyen döngüsel davranışı incelemek için tayf analizi. Örneğin, güneş yerinin 11 yıllık döngüsel değişkenleri. Diğer yaygın kullanılan örnekler, gökyüzü ile ilgili olaylar, hava durumları, sinirsel hareket, mal fiyatları ve ekonomik hareketler.

Açıklama

• Bileşenlerdeki farklılık, yönelimi, mevsimselliği, yavaş ve hızlı değişimi, döngüsel düzensizliği ifade eder.
• Marjinal dağılımların temel özellikleri

Modeller

Zaman seri verisinin modelleri birçok biçimde olabilir ve farklı stokastik işlemleri temsil eder. Bir işlem seviyesinde model değişimleri, elverişli öneminüç genel sınıfları özbağlanımlı modeller (AR), tümleşik (I) modeller ve ortalama hareket (MA) modelleridir. Bu üç model önceki veri noktalarında lineerliğe bağlıdır.

Formül

Zaman seri analizinde kullanılan formüllerden biri şudur:

X = {X₁, X₂, ...}

Bu, zaman serisini ifade eden temel formüldür. Burada X doğal sayılar dizinidir. Diğer yaygın kullanılan formül de şudur:

Y = {Yt: t ∈ T}.

Modeller

Özbağlanımlı modeleni genel ifadesi AR(p) olarak bilinen şudur:

${\displaystyle Y_{t}=\alpha _{0}+\alpha _{1}Y_{t-1}+\alpha _{2}Y_{t-2}+\cdots +\alpha _{p}Y_{t-p}+\varepsilon _{t}\,}$

Burada ε_t terimi rastgelelik kaynağıdır ve beyaz gürültü olarak adlandırılır. Aşağıdaki karakteristikleri gösterdiği varsayılır:

1. ${\displaystyle E[\varepsilon _{t}]=0\,}$

2. ${\displaystyle E[\varepsilon _{t}^{2}]=\sigma ^{2}\,}$

3. ${\displaystyle E[\varepsilon _{t}\varepsilon _{s}]=0\quad \forall t\not =s\,}$

Bu varsayımlar ile işlem, ikinci dereceden fazla zamanla belirtilir ve katsayıdaki şart koşulu, ikinci derece sabiti olur.

Eğer gürültü normal dağılıma sahipse, normal beyaz gürültü olarad adlandırılır (burada Normal-WN olarak gösterilir):

${\displaystyle \{\varepsilon _{t}\}_{(t\in T)}:{\mbox{Normal-WN}}.}$

Bundan dolayı AR işlemi, katsayıdaki şart koşuluna karşı tamamen sabit olabilir.

Ayrıca bakın

• Otokorelasyon

Kaynak

İngilizce Vikipedi'nin w:Time series maddesi