Açı korur simetri

Teorik fizikte, açıkorur simetri (ölçek değişmezi)genişleme ve özel açıkorur dönüşümler altında bir simetridir. Bununla birlikte Poincaré grubu açıkorur simetri grubu üretir.

Üreteçler ve değiştirim ilişkileri

Açıkorur grup gösterimi aşağıdadır:^[1]

${\displaystyle {\begin{aligned}&M_{\mu \nu }\equiv i(x_{\mu }\partial _{\nu }-x_{\nu }\partial _{\mu })\,,\\&P_{\mu }\equiv -i\partial _{\mu }\,,\\&D\equiv -ix_{\mu }\partial ^{\mu }\,,\\&K_{\mu }\equiv i(x^{2}\partial _{\mu }-2x_{\mu }x_{\nu }\partial ^{\nu })\,,\end{aligned}}}$

Burada ${\displaystyle M_{\mu \nu }}$ Lorentz üreteçleridir, ${\displaystyle P_{\mu }}$ üreteçleri ötelemeler, ${\displaystyle D}$ üretim ölçüm dönüşümleri (ayrıca genişlemeler veya genişleme olarak bilinir) ve ${\displaystyle K_{\mu }}$ özel açıkorur dönüşümler üretir.

değiştirim ilişkileri olarak aşağıdakilerdir:^[1]

${\displaystyle {\begin{aligned}&[D,K_{\mu }]=-iK_{\mu }\,,\\&[D,P_{\mu }]=iP_{\mu }\,,\\&[K_{\mu },P_{\nu }]=2i\eta _{\mu \nu }D-2iM_{\mu \nu }\,,\\&[K_{\mu },M_{\nu \rho }]=i(\eta _{\mu \nu }K_{\rho }-\eta _{\mu \rho }K_{\nu })\,,\\&[P_{\rho },M_{\mu \nu }]=i(\eta _{\rho \mu }P_{\nu }-\eta _{\rho \nu }P_{\mu })\,,\\&[M_{\mu \nu },M_{\rho \sigma }]=i(\eta _{\nu \rho }M_{\mu \sigma }+\eta _{\mu \sigma }M_{\nu \rho }-\eta _{\mu \rho }M_{\nu \sigma }-\eta _{\nu \sigma }M_{\mu \rho })\,,\end{aligned}}}$

diğer değiştiriciler kaybolur.

Tensör ${\displaystyle \eta _{\mu \nu }}$ tanımından göz ardı edilir.

Toplanabilirlik, ${\displaystyle D}$ bir ölçek ve${\displaystyle K_{\mu }}$ Lorentz dönüşümleri altında bir eşdeğişir vektördür .

Özel açıkorur(yani bütünsel) dönüşümler ^[2] ile verilir

${\displaystyle x^{\mu }\to {\frac {x^{\mu }-a^{\mu }x^{2}}{1-2a\cdot x+a^{2}x^{2}}}}$

burada ${\displaystyle a^{\mu }}$ dönüşüm tanımlayan bir parametredir.Bu özel açıkorur dönüşüm ayrıca ${\displaystyle x^{\mu }\to x'^{\mu }}$ olarak yazılabilir,burada

${\displaystyle {\frac {{x}'^{\mu }}{{x'}^{2}}}={\frac {x^{\mu }}{x^{2}}}-a^{\mu },}$

Gösterilenler bir tersinin oluşumudur ,bir öteleme ve bir ikinci tersi ile aşağıdadır.

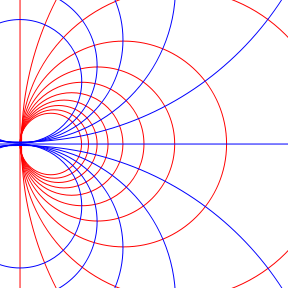
iki boyutlu uzayzaman içinde,açıkorur grupun dönüşümleri açıkorur dönüşümlerdir.

iki boyutludan fazlası içinde, Öklid açıkorur dönüşümler haritası çembere çemberdir, ve hiperkürelere hiperküreler ile bir yumuşak hat bir bozunmuş çember olarak düşünülür ve bir hiperyüzey bir bozunmuş hiperçemberdir.

iki Lorentzyen boyutlar dan daha ötesi içinde, açıkorur dönüşümler haritası boş ışına boş ışın ve ışık koniye ışık koni ile bir boş hiperyüzey bir bozunmuş ışık konisi olacaktır.

Kullanım

Bir süpersimetrik-olmayan büyük olası(global) simetri grubu etkileşim alan teori açıkorur grup ile bir içsel grupun bir doğrudan çarpımıdır.^[3] Böylece teori açıkorur alan teorisi olarak bilinir.

Özel bir uygulama sistemler ile yerel etkileşimleri içinde kritik fenomene ( ikinci düzenin faz ötelemeleri )dir. Bu tür sistemlerde dalgalanmalar kritik noktada açıkorur değişmez kalmaktadır. Yani açıkorur alan teorisi cinsinden faz geçişlerinin evrensellik sınıflarının sınıflandırılması için olanak sağlar.Açıkorur dönüşümü aynı zamanda Reynolds sayısı yüksek iki-boyutlu türbülans keşfedildi.

yüksek-enerji fiziği içindeki birçok teori çalışmaları admit the açıkorur simetriyi kabul eder. Meşhur bir örnek N = 4 için süpersimetrik Yang-Mills teorisidir.Sicim teorisinin dünya sayfası iki-boyutlu çekime perçinlenmiş bir açıkorur alan teorisi olarak tanımlıyor.

Ayrıca bakınız

• Coleman–Mandula teoremi
• Renormalizasyon grubu
• Ölçek değişmezi
• Süper açıkorur cebir
• Harry Bateman
• Ebenezer Cunningham

Kaynakça

1. Di Francesco; Mathieu, Sénéchal (1997). Conformal field theory. Graduate texts in contemporary physics. Springer. s. 98. ISBN 978-0-387-94785-3. 
2. Di Francesco; Mathieu, Sénéchal (1997). Conformal field theory. Graduate texts in contemporary physics. Springer. s. 97. ISBN 978-0-387-94785-3. 
3. Juan Maldacena; Alexander Zhiboedov (2013). "Constraining conformal field theories with a higher spin symmetry". Journal of Physics A: Mathematical and Theoretical 46 (21): 214011. DOI:10.1088/1751-8113/46/21/214011. http://inspirehep.net/search?p=recid:1079967&of=hd.