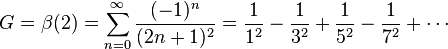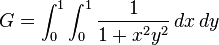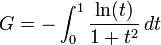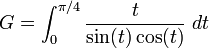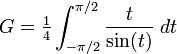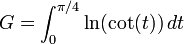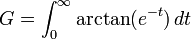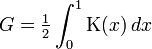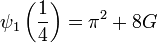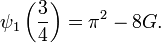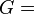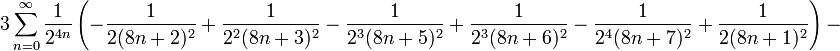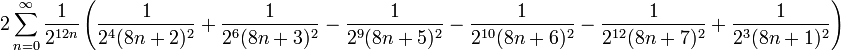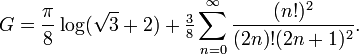Catalan sabiti

Catalan sabiti matematikte bazen kombinatorik'te tahminler için kullanılır.Tanımı

$G = \beta(2) = \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2n+1)^2} = \frac{1}{1^2} - \frac{1}{3^2} + \frac{1}{5^2} - \frac{1}{7^2} + \cdots \!$

Burada β Dirichlet beta fonksiyonu'dur Sayısal değeri yaklaşık olarak

G = 0.915 965 594 177 219 015 054 603 514 932 384 110 774 …

G nin rasyonel veya irrasyonel olup olmadığı bilinmiyor. Catalan sabiti Eugène Charles Catalan onuruna atfedilmiştir.

Integral özdeşlikleri

Bazı eşitlikler arasında

$G = \int_0^1 \int_0^1 \frac{1}{1+x^2 y^2} \,dx\, dy \!$

$G = -\int_{0}^{1} \frac{\ln(t)}{1 + t^2} \,dt \!$

$G = \int_{0}^{\pi/4} \frac{t}{\sin(t) \cos(t)} \;dt \!$

$G = \tfrac14 \int_{-\pi/2}^{\pi/2} \frac{t}{\sin(t)} \;dt \!$

$G = \int_{0}^{\pi/4} \ln ( \cot(t) ) \,dt \!$

$G = \int_{0}^{\infty} \arctan (e^{-t}) \,dt \!$

$G = \int_0^1 \frac{\arctan t}{t}\,dt \!$.

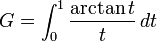ile birlikte

$G = \tfrac12\int_0^1 \mathrm{K}(x)\,dx \!$

burada K(x) komplet eliptik integral'in ilk türüdür., ve

$G = \int_0^1 \frac{\arctan x}{x}\,dx \!$.

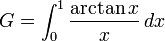Kullanımı

Poligama fonksiyonu'ndan elde edilen ve trigama fonksiyonu olarak adlandırılan

kombinatorik'teki G nesnesinin fraksiyonel gösterimi;

$\psi_{1}\left(\frac{1}{4}\right) = \pi^2 + 8G$

$\psi_{1}\left(\frac{3}{4}\right) = \pi^2 - 8G.$

şeklindedir.

Simon Plouffe 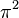$\pi^2$ ve Catalan sabiti arasında trigamma fonksiyonunun sonsuz sayıda eşdeğer koleksiyonun'un olduğunu grafik yolu ile gösterdi.

Ayrıca bu nesnenin hiperbolik sekant dağılımı ile de bağlantısı vardır

Hızlı yakınsak seri

sayısal hesaplama için kolay olan birbirini izleyen iki hızlı yakınsak seri

$G = \,$	$3 \sum_{n=0}^\infty \frac{1}{2^{4n}} \left( -\frac{1}{2(8n+2)^2} +\frac{1}{2^2(8n+3)^2} -\frac{1}{2^3(8n+5)^2} +\frac{1}{2^3(8n+6)^2} -\frac{1}{2^4(8n+7)^2} +\frac{1}{2(8n+1)^2} \right) -$
	$2 \sum_{n=0}^\infty \frac{1}{2^{12n}} \left( \frac{1}{2^4(8n+2)^2} +\frac{1}{2^6(8n+3)^2} -\frac{1}{2^9(8n+5)^2} -\frac{1}{2^{10} (8n+6)^2} -\frac{1}{2^{12} (8n+7)^2} +\frac{1}{2^3(8n+1)^2} \right)$

ve

$G = \frac{\pi}{8} \log(\sqrt{3} + 2) + \tfrac38 \sum_{n=0}^\infty \frac{(n!)^2}{(2n)!(2n+1)^2}.$

Bunun teoretik çıkarımı Broadhurst tarafından verilmiştir.

Basamaklardaki rakamların çıkarımı

Catalan sabiti G nin rakamlarını bulmak için son yıllarda çarpıcı bir artış var.Bunun için yüksek performanslı bilgasayarlar ve güçlü algoritmalar geliştiriliyor.^[1]

G nin onluk sistemde bilinen rakam sayısı

Tarih	Onluk sistem	Çaba harcayanlar
1877	20	James W. L. Glaisher
1913	32	James W. L. Glaisher
1990	20,000	Greg J. Fee
1996	50,000	Greg J. Fee
August 14, 1996	100,000	Greg J. Fee & Simon Plouffe
September 29, 1996	300,000	Thomas Papanikolaou
1996	1,500,000	Thomas Papanikolaou
1997	3,379,957	Patrick Demichel
January 4, 1998	12,500,000	Xavier Gourdon
2001	100,000,500	Xavier Gourdon & Pascal Sebah
2002	201,000,000	Xavier Gourdon & Pascal Sebah
October 2006	5,000,000,000	Shigeru Kondo & Steve Pagliarulo[2]
August 2008	10,000,000,000	Shigeru Kondo & Steve Pagliarulo[3]
January 31, 2009	15,510,000,000	Alexander J. Yee & Raymond Chan[4]
April 16, 2009	31,026,000,000	Alexander J. Yee & Raymond Chan[4]

Ayrıca bakınız

• Zeta sabiti

Notlar

1. Gourdon, X., Sebah, P; Constants and Records of Computation
2. Shigeru Kondo's website
3. Constants and Records of Computation
4. Large Computations

Kaynakça

• Victor Adamchik, 33 representations for Catalan's constant (undated)
• Victor Adamchik, A certain series associated with Catalan's constant, (2002) Zeitschrift fuer Analysis und ihre Anwendungen (ZAA), 21, pp. 1–10.
• Simon Plouffe, A few identities (III) with Catalan, (1993) (Provides over one hundred different identities).
• Simon Plouffe, A few identities with Catalan constant and Pi^2, (1999) (Provides a graphical interpretation of the relations)
• Eric W. Weisstein, Catalan's Constant (MathWorld)
• Catalan constant: Generalized power series at the Wolfram Functions Site
• Greg Fee, Catalan's Constant (Ramanujan's Formula) (1996) (Provides the first 300,000 digits of Catalan's constant.).