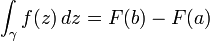Cauchy integral teoremi
Matematiğin bir dalı olan karmaşık analizde, Augustin Louis Cauchy'nin ismine atfedilen Cauchy integral teoremi, karmaşık düzlemdeki holomorf fonksiyonların çizgi integralleri hakkında önemli bir teoremdir. Esasen, teoremin ifade ettiği şudur: İki ayrı yol aynı iki noktayı birbirine bağlıyorsa ve bir fonksiyon bu iki ayrı yolun arasındaki iç bölgede holomorfsa, o zaman fonksiyonun bu iki yol integrali birbirine eşittir.
Teorem, kapalı yollar için ise şu şekilde ifade edilir. U, C 'nin basit bağlantılı açık bir altkümesi olsun. f : U → C holomorf bir fonksiyon olsun ve γ, U içinde başlangıç noktası bitiş noktasıyla aynı olan doğrultulabilir bir yol olsun. O zaman
eşitliği vardır.
Goursat tarafından gösterildiği gibi, Cauch integral teoremi, U içinde her yerde f 'nin karmaşık türevi olan f '(z) varsa, kanıtlanabilir. Bu önemlidir çünkü bu fonksiyonlar için o zaman Cauchy integral formülü de kanıtlanabilir ve bundan aslında bu fonksiyonların sonsuz kere türevlenebilmesi özelliği çıkar.
U 'nun basit bağlantılı olması koşulu U 'da "delik" olmaması anlamına gelir veya homotopi kavramlarıyla tartışılacak olursa , U 'nun temel grubunun bariz olması demektir. Örneğin, 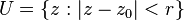 açık diski bunlardan biridir. Bu şart teoremde çok önemlidir. Birim çemberi dolaşan
açık diski bunlardan biridir. Bu şart teoremde çok önemlidir. Birim çemberi dolaşan
düşünüldüğünde,
yol integrali sıfır olmayacaktır. Cauchy integral teoremi, f(z) = 1/z fonksiyonu z = 0 noktasında tanımlı olmadığı (ve tabi holomorf olmadığı) için artık burada geçerli değildir.
Teoremin önemli sonuçlarından birisi basit bağlantılı bölgelerdeki holomorf fonksiyonların yol integrallerinin hesabın temel teoremindekine benzer bir şekilde hesaplanabilmesidir: U, C 'nin basit bağlantılı açık bir kümesi olsun. f : U → C holomorf bir fonksiyon olsun ve γ, başlangıç noktası a, bitiş noktası b olan bir parçalı sürekli türevlenebilir yol olsun. F, f 'nin karmaşık antitürevi ise, o zaman
eşitliği vardır.
Cauchy integral teoremi üstte verilen halinden biraz daha güçlü halde de geçerlidir. U 'nun sınırı doğrultulabilir bir yolun (mesela γ) görüntüsü olsun ve ayrıca U basit bağlantılı açık bir C altkümesi olsun. f, U üzerinde holomorf olan bir fonksiyonsa ve U 'nun kapanışında sürekliyse, o zaman
eşitliği vardır.
Cauchy integral teoremi ayrıca Cauchy integral formülü 'nün ve rezidü (kalıntı) teoreminin kanıtlanmasını da sağlar.
Ayrıca bakınız
- Cauchy-Riemann denklemleri
- Cauchy integral formülü
- Morera teoremi
- Kontür integrali metotları
- Kalıntı (karmaşık analiz)
Dış bağlantılar
- http://mathworld.wolfram.com/CauchyIntegralTheorem.html MathWorld'deki ilgili sayfa.
- Cauchy-Goursat Teoremi Modülü, John H. Mathews tarafından
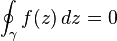
![\gamma(t) = e^{it} \quad t \in \left[0,2\pi\right]](../I/m/8b5eef698c00b09b32a08b0a02e7cd73.png)