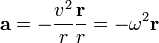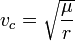Dairesel yörünge

Farklı kütle ve yarıçapa sahip iki cisim konum olarak uzaydaki bir boşlukta bulunan ortak kütle merkezleri etrafında dairesel yörüngelerinde hareket ederken görülüyor.

Uzay mekaniğinde dışmerkezliği sıfıra eşit olan eliptik yörünge olarak özetlenebilecek dairesel yörünge, tanım olarak fizikte sabit eksen etrafında rotasyonun tipik bir örneğidir. Burada bahsedilen eksen, hareket düzlemine dik olarak kütle merkezlerinden geçen doğrudur.

Dairesel ivme

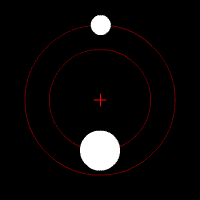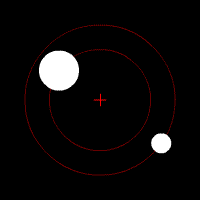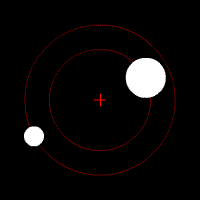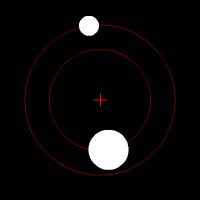
Kütleçekim tarafından yaratılan merkezcil ivme (hareket yönüne dik enine veya özekçil ivme), yörüngede aslında düz bir doğru boyunca ilerlemek isteyen cismin yönünü sürekli olarak aynı miktarda ve sürede değiştirerek kütle merkezi etrafında bir dairesel veya eliptik hareket etmesini sağlar. Merkezcil ivmeyi bulabilmek için aşağıdaki formül kullanılabilir.

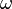\mathbf{a} = - \frac{v^2}{r} \frac{\mathbf{r}}{r} = - \omega^2 \mathbf{r}

Burada,

$v\,$ yörüngeyi çizen küçük cismin yörüngesel hızı,
$r\,$ çizilen dairenin yarıçapı
$\omega \$ ise (radyan/saniye cinsinden) açısal frekansı ifade eder.

Hız

Uzay mühendisliğince kabul edilen standart şartlar ve varsayımlar altında, dairesel yörüngede hareket halinde bulunan 0'dan büyük kütleli bir cismin yörüngesel hızı (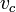 $v_c\,$ ) aşağıdaki şekilde hesaplanabilir.

v_c=\sqrt{\mu\over{r}}

Burada,

$r\,$ yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafeye eşit olan yarıçap,
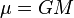$\mu=GM\,$ ise standart kütleçekim değişkenidir. Bu değer evrensel kütleçekim sabiti $G$ ile merkezi kütlenin $M$ çarpımına eşittir.

Not: Bu eşitlikten çıkartılması gereken en önemli sonuç, dairesel yörüngede hareket eden bir cismin yörünge boyunca bulunduğu nokta veya konum her ne olursa olsun hızının daima aynı ve sabit kalacağı olmalıdır.

Yörüngesel periyot

Standart şartlar ve varsayımlar altında, dairesel yörüngede hareket eden bir cismin yörüngesel periyodu ( $T\,\!$ ),

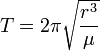T=2\pi\sqrt{r^3\over{\mu}}

formülü ile hesaplanabilir. Burada,

$r\,$ yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafeye eşit olan yarıçap,
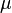$\mu\,$ ise standart kütleçekim değişkenidir.

Enerji

Standart şartlar ve varsayımlar altında yörüngesel enerji ( $\epsilon\,$ ), kapalı bir yörünge için eksidir (-) ve enerji korunum yasası gereği yörüngesel enerji,

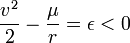{v^2\over{2}}-{\mu\over{r}}=\epsilon< 0

formunu alacaktır. Burada,

$v\,$ cismin yörüngesel hızı,
$r\,$ yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafeye eşit olan yarıçap,
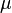$\mu\,$ ise standart kütleçekim değişkenidir.

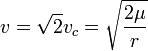Burada limit $\epsilon\,=0$ 'dır ve bu cismin parabolik yörüngeden $v=\sqrt{2}v_c=\sqrt{2\mu\over{r}}$ ile kaçışını ifade eder..

Halkalanma teoremi burada zaman ortalamaları alınmadan dahi geçerlidir.

Sistemin potansiyel enerjisi toplam enerjinin iki katına eşittir.
Sistemin kinetik enerjisi toplam enerji çarpı (-1)'e eşittir.

Elbette bu durumda herhangi bir mesafeden kurtulma hızı, √2 çarpı dairesel yörüngede o mesafedeki hızıdır. Kinetik enerji ise bunun iki katıdır ve o yüzden sistemin toplam enerjisi sıfıra eşittir (kapalı sistem).

Hareket eşitliği

Standart şartlar ve varsayımlar altında yörüngesel eşitlik kısaca

r={{h^2}\over{\mu}}

şeklinde ifade edilir. Burada,

$r\,$ yörüngedeki cisim ile merkezi kütle arasındaki radyal mesafe,
$h\,$ yörüngedeki cismin açısal momentumu (açısal devinirlik),
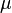$\mu\,$ de standart kütleçekim değişkenidir.

Dairesel bir yörüngeye girmek için gereken delta-v

Belirli bir yersabit yörüngeye manevra yapabilmek için gereken delta-v, bir kurtulma yörüngesi için gereken delta-v`den fazladır. Bu konuda ayrıntıli bilgi için Hohmann geçiş yörüngesine göz atınız.

Ayrıca bakınız

This article is issued from Vikipedi - version of the 3/2/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.