Dizi hizalaması

Biyoenformatikte dizi hizalaması, DNA, RNA veya protein dizilerini düzenleyerek benzer bölgelerin tespit edilmesidir. Bu bölgelerin benzer olması, diziler arasında işlevsel, yapısal veya evrimsel bir ilişki olduğu anlamına gelir.[1] Hizalanmış nükleotit veya aminoasit kalıntı dizileri tipik olarak bir matriksin satırları olarak gösterilir. Kimyasal kalıntıları temsil eden harflerin arasına boşluklar konarak ardışık sütunlarda yer alan aynı veya benzer harflerin bir hizada olması (altalta gelmesi) sağlanır.

Dizi hizalaması biyolojik olmayan dizilerde, örneğin doğal dil veya finansal verilerde de kullanılabilir.

Yorumlama

İki dizi ortak bir ataya sahipse, hizalamada eşleşmeyen harfler, bu dizilerin birbirinden ıraksadığı zamandan beri meydana gelmiş noktasal mutasyonlar olarak yorumlanır. Hizalamadaki boşluklar ise insersiyon veya delesyonlar (indel) olarak yorumlanır. Proteinlerin dizi hizalamasında belli bir pozisyondaki amino asitlerin benzerlik derecesi, bu proteinler için belli bir bölge veya dizi motifininin ne kadar korunmuş olduğunun kaba bir ölçütü olarak alınabilir. Dizinin belli bir bölgesinde substitusyonların olmaması veya sadece çok muhafazkar substitusyonların olması (yani benzer biyokimyasal özelliğe sahip amino asit substitusyonları), bu bölgenin yapısal veya işlevsel bir öneme sahip olduğunun bir belirtisi sayılır.[2] DNA ve RNA bazları, proteinlerdeki aminoasitlerden daha çok birbirine benzese de, baz çiftlerinin korunması da benzer bir işlevsel veya yapısal önemi belirtebilir.

Hizalama yöntemleri

Çok kısa veya çok benzer diziler elle hizalanabilir. Ancak, çoğu ilginç problem, insan eliyle yapılamıyacak kadar uzun, karmaşık veya çok sayıda dizinin hizalanmasını gerektirir. Böyle durumlarda, kaliteli dizi hizalamaları elde edebilmek için insan bilgisine dayanan algoritmalar kullanılır. Ender olarak bu algoritmalardan elde edilen sonuçlar, algoritmik olarak ifadesi zor olan durumlar için elle düzeltilebilir. Dizi hizalaması için kullanılan hesaplamalı yöntemler genelde iki gruba ayrılır: global optimizasyon ve yerel optimizasyon. Global hizalamanın bulunması bir global optimizasyon çeşididir ve elde edilecek hizalamanın, sorgulanan dizilerin tamamını kapsamaya "zorlar". Buna karşın, yerel hizalamalar genelde birbirinden çok farklılık gösteren uzun dizilerde benzer bölgeleri tespit eder. Çoğu zaman yerel hizalamalar tercih edilir ama bunların bulunması daha zor olabilir. Dizi hizalama problemi için çeşitli algoritmalar uygulanmıştır, bunların bazıları, dinamik programlama gibi, yavaş ama formel olarak eniyileyici yöntemlerdir, bazıları ise hızlı ama mutlaka mükemmel sonucu vermeyebilen, veri tabanı aramaları için tasarlanmış buluşsal algoritmalar veya olasılıksal yöntemlerdir.

Temsil biçimleri

Hizalamalar genelde hem grafik olarak hem de metin olarak gösterilir. Hemen her dizi hizalama gösteriminde diziler satırlar şeklinde ve hizalanmış harfler de sütunlar halinde düzenlenir. Metin formatlarında aynı veya benzer harfler içeren hizalanmış sütunlar korunma sembolleri ile gösterilir. Yukarıdaki resimde olduğu gibi, bir yıldız veya dik çizgi iki satır arasındaki aynılığı göstermekte kullanılır; daha ender kullanılan semboller ise, korunmuş bir substitusyon için iki nokta üstüste, ve yarı korunmuş substitusyonlar için bir noktadır. Çoğu dizi görüntüleme programları ayrıca substitusyon harflerinin özelliklerini belirtmek için renkler kullanır; DNA ve RNA dizilerinde her nükleotidin kendi rengi olur. Protein hizalamalarında, örneğin yukarıdaki örnekte olduğu gibi, belli bir amino asit substitusyonunu korunumunu değerlendirmek için renk kullanılır. Çoklu dizilerde her sütünun son satırı o hizalama ile belirlenmiş olan konsensus dizisidir; konsensus dizinin grafik olarak gösterilmesi bir dizi logosu ile olur; dizi logosunda her nükleotit veya amino asitin harfinin büyüklüğü o harfin korunma derecesine karşılık gelir.[3]

Dizi hizalamaları çeşitli metin-tabanlı dosya formatlarında saklanabilir, bunların çoğu ilk olarak belli bir hizalama programı veya uygulaması ile birlikte geliştirilmiştir. Çoğu Web-temelli araçlar sınırlı sayıda girdi ve çıktı format seçeneği verirler, örneğin FASTA formatı ve GenBank formatı gibi, ve program çıktısı genelde kolayca değiştirilemez. Çeşitli format dönüştürme programları mevcuttur, bunlardan READSEQ ve EMBOSS gibi bazılarının grafik arayüzü veya komut satır arayüzü vardır, buna karşın BioPerl, BioRuby gibi program paketlerinin buna olanak veren kendi fonksiyonları vardır.

Global ve lokal hizalamalar

Global hizalamalarda her dizideki her harfin hizalanması amaçlanır. Sorgu kümesindeki diziler birbirine benzer ve yaklaşık aynı uzunlukta olursa global hizalamaları en yararlı olur. (Ama bu, global hizalamaların boşluklarla sonlanamayacağı anlamına gelmez.) Global hizalama tekniklerinden biri, dinamik programlamaya dayalı olan Needleman-Wunsch algoritmasıdır. Birbirine benzemeyen ama benzer bölgeler içerdiği tahmin edilen diziler için lokal hizalamalar daha yararlıdır. Keza, benzer kısa dizi motiflerinin tespitinde lokal hizalamalar kullanılır. Smith-Waterman algoritması da dinamik programlamaya dayalı bir lokal hizalama yöntemidir. Eğer diziler yeterince birbirine benziyorsa lokal ve global hizalama sonuçları arasında bir fark olmaz.

Hibrit yöntemler (yarı global veya "glokal" yöntemler olarak da adlandırılabilir) bir veya öbür dizinin başı ve sonunu da kapsayan en iyi hizalamayı bulmaya çalışır. Dizilerden birinin sonu, öbürünün başı ile örtüşüyorsa bu özellikle yararlı olabilir. Bu durumda ne global ne de lokal hizalama tamamen uygundur: global yöntem hizalamayı örtüşme bölgesinin dışına uzatmaya çalışacaktır, lokal yöntem ise örtüşme bölgesini yeterince kapsamayabilir.[4]

İkili hizalama

İkili hizalama yöntemleri, iki sorgu dizisinin birbiriyle en iyi uyuşan parçalı (lokal) veya global hizalamasını bulmakta kullanılır. İkili hizalamalar bir defada sadece iki dizi arasında bulunabilir ama hesaplanmaları verimlidir ve çoğu zaman çok yüksek doğruluk gerektirmeyen yöntemlerde kullanılırlar (örneğin bir veritabanında sorgu dizisine yüksek oranda benzeyen dizileri bulmak için). İkili hizalamalar üretmekte kullanılan üç ana yöntem, nokta-matris yöntemleri, dinamik programlama ve sözcük yöntemleridir;[1] ancak, çoklu hizalama yöntemlerinde de dizi ikilileri hizalanır. Her yöntemin kendi avantaj ve dezavantajları olsa da, bu ikili hizlama yöntemlerinin hepsi, düşük bilgi içerikli olan çok tekrarlı dizilerde zorlanırlar, özellikle hizalanacak olan iki dizideki tekrarlı altdizilerin sayıları farklıysa. Belli bir ikili hizalama yönteminin yararını nicelemenin bir yolu, 'maksimum yegane uyuşma' yani her iki dizide bulunan en uzun altdizidir. Daha uzun ortak altdiziler tipik olarak daha yakın bir ilişkiyi yansıtır.

Nokta matris yöntemleri

Bir insan çinko parmak transkripsyon faktörünün (GenBank ID NM_002383) nokta matris grafiği, bölgesel öz-benzerlik göstermektedir. Ana çapraz, dizinin kendizi ile hizalanmasını temsil etmektedir; ana çaprazın dışında yer alan çizgiler birbirinin aynı (veya birbirine benzer) tekrarlı altdizilerdir. Bu grafik, tekrarlılık grafiğinin (recurrence plot) tipik bir örneğidir.

Nokta matris yaklaşımında her bir dizi bölgesi için hizalama aileleri üretilir. Bu yöntem nitel ve basittir ama büyük ölçekte analiz etmesi zaman alıcıdır. İnsersiyon, delesyon, tekrar ve ters dönmüş tekrar (inverted repeats) gibi bazı dizi özelliklerinin görsel tespiti çok kolaydır. Bir nokta matrisi oluşturmak için iki dizi, iki boyutlu bir matrisin üst satırı ve sol sütunu boyunca yazılır, sonra eğer bir satır ve sütunun başındaki harfler aynıysa kesişim yerine bir nokta konur. Bu yaklaşımın bazı uygulamalarında iki harfin benzerlik derecesiyle orantılı büyüklükte bir nokta konur, korunmalı substitusyonları hesaba katabilmek için. Birbirine çok benzeyen dizilerin nokta matrisleri, matrisin ana çaprazı boyunca giden tek bir çizgi gibi görünür.

Nokta matris grafikleri (İng. dot plot) tek bir dizi içindeki tekrarlılık miktarını belirlemekte de kullanılabilir. Bir dizi kendi kendisi ile grafiklenir, birbirine önemli derecede benzerlik gösteren bölgeler ana çaprazın yanlarında çizgiler olarak görünür. Proteinin birden çok benzer yapısal bölgeden oluşması durumunda bu görülebilir.

Dinamik programlama

Dinamik programlama tekniği, Needleman-Wunsch algoritması ile global hizalamalar üretmek için, Smith-Waterman algoritması ile de lokal hizalamalar üretmek için uygulanabilir. Tipik kullanımda, protain hizalamalarında amino asit uyuşma veya uyuşmamalarına bir skor verebilmek için bir substitusyon matrisi; bir dizideki amino asitin öbür dizide bir boşlukla eşleştirilmesi için de bir boşluk ceza değeri kullanılır. DNA ve RNA hizalamaları bir skor matrisi kullanabilir ama pratikte basitçene pozitif bir uyuşma skoru, negatif bir uyuşmama skoru ve negatif bir boşluk cezası verilir. (Standart dinamik programlamada, her amino asitin skoru komşularının kimliğinden bağımsızdır, dolayısıyla baz istiflemesi etkileri hesaba katılmaz. Ancak, algoritmayı değiştirip bu tür etkileri de göz önüne almak mümkündür.)

Standart doğrusal boşluk cezası yerine bazı algoritmalarda kullanılan bir varyasyon, iki ayrı boşluk cezası uygulamadır: biri boşluğu açmak içindir, öbürü ise boşluğu uzatmak içindir. Tipik olarak birinci cezanın değeri ikincisinden daha büyüktür, örneğin boşluk açmak için -10 puan, boşluk uzatmak için -2 puan kullanılabilir. Bunun sonucu olarak, bir hizalamadaki boşluk sayısı azalır, harfler ve boşluklar bir arada tutulmuş olur, bu da biyolojik bakımdan daha gerçekçi sayılır. Gotoh algoritması, üç matris kullanarak 'affin' boşluk cezalarını hesaplar.

Dinamik programlama nükleotit dizilerini protein dizileri ile hizalamaya yarayabilir. Bu, karmaşık bir iş olabilir çünkü çerçeve kayması mutasyonlarının (genelde insersiyon ve delesyonlar) etkisini hesaba katmak gerekir. Çerçeve arama yöntemi kullanılarak bir nükleotit sorgu dizisi ile protein dizilerinden oluşan arama kümesi arasında (veya tersi) global veya lokal ikili hizalamalar üretilir. Bu yöntem çok yavaş olmasına rağmen, çerçeve kaymalarını değerlendirme yeteneği, çok sayıda "indel"ler (insersiyon ve delesyonlar) içeren diziler için çok yararlıdır. Bu tür dizilerin normalde verimli çalışan buluşsal (höristik) yöntemlerle hizalanması çok zordur. Pratikte, bu yöntem yüksek hesaplama gücü veya dinamik programlama için özelleşmiş mimariye sahip bir bilgisayar sistemi gerektirir. BLAST ve EMBOSS paketleri, çevrimli (translasyonlu) hizalamalar yapmak için temel araçlara sahiptir (gerçi bunların bazılarının, bu programların arama yeteneklerinin yan etkilerinden yararlandığı söylenebilir). Daha genel yöntemler Accelrys'in GCG paketi'ndeki FrameSearch gibi ticari kaynaklardan ve Genewise gibi bazı açık yazılım ürünlerinden elde edilebilir.

Dinamik proramlama yöntemi belli bir skorlama fonksiyonu için optimal hizalamayı bulmayı garantiler. Ancak, iyi bir skorlama fonksiyonunu belirlemek çoğu zaman teorik değil, empirik bir meseledir. Dinamik programlara ikiden çok diziye de genellenebilirse de, çok sayıda dizi veya çok uzun dizilerde kullanılamayacak derecede yavaş çalışır.

Sözcük yöntemleri

Sözcük yöntemleri, k-li yöntemler olarak da bilinir, optimal hizalama çözümünü bulması garantili olmayan, ama dinamik programlamadan önemli derecede daha verimli olan höristik yöntemlerdir. Bu yöntemler büyük ölçekli veritabanlarında özellikle yararlıdır, çünkü bu veritabanlarındaki aday dizilerin büyük bir kısmının sorgu dizisiyle anlamlı bir uyuşma göstermeyeceği peşinen bilinmektedir. Sözcük yöntemleri, veritabanı arama araçları olan BLAST ailesi üyelerindeki ve FASTA programındaki uygulamaları ile bilinirler.[1] Sözcük yöntemleri sorgu dizisinde bulunan kısa, örtüşmeyen altdizileri ("sözcükleri") tespit edip bunları veritabanındaki aday dizilerle eşleştirir. Bir sözcüğün iki dizideki pozisyonları arasındaki fark hesaplanarak bir kayma değeri elde edilir. Eğer farklı sözcükler aynı kayma değerine sahipse bu kayma değeri bir hizalanma bölgesini belirler. Ancak eğer böyle bir bölge bulunursa, o zaman daha hassas hizalama kıstasları uygulanır. Böylece kayda değer benzerlik göstermeyen diziler arasında pek çok gereksiz karşılaştırmanın önüne geçilmiş olur.

FASTA yönteminde kullanıcı, veritabanını aramakta kullanılacak sözcüğün uzunluğuna karşılık gelen bir k değeri seçer. Küçük k değerlerinde yöntem daha yavaş ama daha duyarlıdır, bunlar kısa sorgu dizileri için tercih edilir. BLAST ailesindeki araştırma yöntemleri, belli sorgu tipleri (örneğin uzaktan ilişkili dizilerin bulunması) için optimize edilmiş çeşitli algoritmalara sahiptir. BLAST, FASTA'dan daha hızlı olup doğruluktan çok az bir fedakarlık yapma özelliği için geliştirilmiştir. FASTA gibi BLAST da k uzunluklu bir sözcük araması yapar ama sadece en önemli sözcük uyuşmalarını değerlendirir, FASTA gibi her sözcük uyuşmasına bakmaz. Çoğu BLAST uygulamasında varsayılan sözcük uzunluğu değişmez, sorgu ve arama tipine göre optimize edilir, ancak istisnai durumlarda, tekrarlı dizileri ararken veya kısa sorgu dizileri için değiştirilir. BLAST çeşitli Web portallarında bulunabilir, örneğin EMBL FASTA and NCBI BLAST.

Çoklu dizi hizalaması

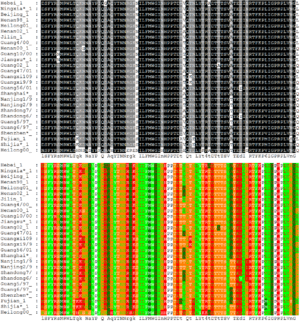
27 adet kuş enfluenza virüsü hemaglutinin protein dizisinin hizalanması, amino asit kalıntılarının korunması (üstte) veya özelliklerine (altta) göre renklendirilmiştir.

Çoklu dizi hizalaması ikiden daha fazla dizi içermesiyle ikili hizalamanın bir uzantısı sayılır. Çoklu dizileme yöntemleri sorgu kümesindeki tüm dizileri hizalamaya çalışır. Çoklu hizalamalar çoğu zaman birbiriyle evrimsel ilişkisi olduğu hipotez edilen bir grup dizideki korunmuş bölgeleri tespit etmek için kullanılır. Bu tür hizalamalar ayrıca filogenetik ağaç inşa ederek evrimsel bir ilişkiyi ortaya koymak için kullanılır. Böylesi korunmuş diziler, yapısal ve mekanistik bilgilerle beraber kullanılarak enzimlerin katalitik aktif bölgesinin yerini bulmaya yarar. Çoklu dizi hizalamaların üretimi berimsel bakımdan zordur ve bu problemin çoğu formülasyonu NP-tam kombinatoryal optimizasyon problemlerine dönüşür.[5] Buna rağmen, bu hizalamaların biyoinformatikteki faydaları nedeniyle 3 veya daha fazla dizinin hizalanmasını sağlıyan çeşitli yöntemler geliştirilmiştir.

Dinamik programlama

Dinamik progrmalama tekniği herhangi sayıda dizi için kullanılabilir. Ancak, berimsel olarak hem zaman hem bellek bakımından pahalı olduğu için, en basit biçimiyle dahi üç veya dört tane diziden fazlası için kullanılmaz. Bu yöntem iki dizinin hizalanmasında yaratılan matrisin n-boyutlu karşılığının inşasını gerektirir, burada n, sorgu kümesindeki dizi sayısıdır. Sorgu dizilerindeki her bir dizi çifti için standart dinamik programlama kullanılır, sonra bu ara çözümler arasındaki uyuşmalar veya boşluklar değerlendirilerek "hizalama uzayı" tamamlanır, yani her iki dizili hizalama arasında bir hizalama yapılmış olur. Bu yöntem berimsel olarak pahalı olsa da, global optimal çözümü üreteceğini garantiler, bu yüzden az sayıda dizinin hatasız hizalanması gerektiğinde faydalıdır. Berimsel karmaşıklığı azaltılmasını bir yolu "çiftler toplamı" adlı objektif fonksiyona dayanır, bu yaklaşım MSA yazılım programında uygulanmıştır.[6]

İlerlemeci yöntemler

İlerlemeci, hiyerarşik veya ağaç yöntemleri, birbirine en benzer dizileri hizalamakla başlar, sonra gittikçe daha az benzeyen dizilerin hizalamaya eklenmesi ile sonunda tüm sorgu kümesi sonuca dahil edilir. Dizilerin yakınlığını betimleyen ağaç yapısı ikili kıyaslamalara dayanır, bunlar FASTA gibi höristik ikili hizalama yöntemleri kullanır. İlerlemeci hizalama sonuçları "en benzer" dizilerin seçimine bağımlıdır, bu yüzden ilk yapılan ikili hizalamadaki hatalara duyarlıdır. Çoğu ilerlemeci, çoklu dizi hizalama yöntemi buna ek olarak, sorgu kümesindeki diziler arasındaki yakınlık drecesine göre onlara ağırlık verir, böylece ilk dizilerin kötü seçilmesi olasılığı azalır ve en son hizalamanın doğruluğu iyileşir.

Clustal ilerlemeci uygulamalarının çoğu varyasyonu[7][8][9] çoklu dizi hizalaması, filogenetik ağaç inşası ve protein yapı hesaplamasına girdi hazırlamakta kullanılır. İlerlemeci yöntemin daha yavaş ama daha doğruluklu bir varyantı T-Coffee[10] olarak adlandırılır. Bu algoritmaların uygulamaları ClustalW ve T-Coffee'de bulunabilir.

Tekrarlayıcı yöntemler

İlerlemeci yöntemlerin zayıf bir yönü, ilk ikili hizalamanın doğru olmasına olan büyük bağımlılıktır. Tekrarlayıcı yöntemler, bunu iyileştirmeye çalışırlar. Tekrarlayıcı yöntemler seçilmiş bir skorlama fonksiyonuna dayanan objektif fonksiyonu optimize ederler, ilk global hizalamayı oluşturup sonra dizi altkümelerini yeniden hizalayarak. Yeniden hizalanan altkümelerin kendileri de hizalanarak çoklu dizi hizalamasının bir sonraki yinelemesini oluştururlar. Dizi altkümelerini ve objektif fonksiyonu seçmek için çeşitli yollar mevcuttur.[11]

Motif keşfi

Motif bulmak, veya profil analizi, sorgu kümesindeki dizilerde bulunan kısa, korunmuş dizi motiflerini hizalamaya çalışan, global çoklu dizi hizalamaları inşa eder. Önce bir global dizi hizalaması inşa edilir, sonra yüksek derecede korunmuş bölgeler tespit edilir ve bunlar bir profil matrisi oluşturmak için kullanılır. Her korunmuş bölgenin profil matrisi bir skorlama matrisi gibi düzenlenmiştir ama, her pozisyondaki harf için frekans sayıları, korunmuş bölgedeki harf dağılımından elde edilmiştir, daha genel bir dağılımdan değil. Bunun ardından, profil matrisleri betimledikleri motifi başka dizilerde aramak için kullanılırlar. Orijinal veri kümesinde az sayıda dizi olması veya bu dizilerin birbiriyle çok yakın ilişkili olması hâlinde, motifte temsil edilen harf dağılımını normalize etmek için sahte sayımlar eklenir.

Bilgisayar biliminde esinlenmiş yöntemler

Bilgisayar biliminde yaygın kullanılan çeşitli optimizasyon algoritmaları çoklu dizi hizalama problemine uygulanmıştır. Gizli Markov modelleri belli bir sorgu kümesi için olasıl çoklu dizi hizalamaları için olasılık skorları üretmek için kullanılır. Bu yaklaşımla çalışan ilk uygulamalar hayal kırıcı olduysa da, daha sonrakilerin uzaktan ilişkili dizilerin tespitinde özellikle etkili olduğu bulunmuştur, çünkü bu yöntemler korunmuş veya yarı korunmuş substitusyonların yarattığı gürültüden kolay etkilenmemektedirler.[12] Genetik algoritmalar ve benzetilmiş tavlama da çoklu dizi hizalama skorlarını optimize etmekte kullanılmıştır. Bu konuda daha çok ayrıntı çoklu dizi hizalaması hakkındaki maddede bulunabilir.

Yapısal hizalama

Yapısal hizalamalar genelde protein ve bazen RNA dizileri için yapılır, dizileri hizalamak için protein ve RNA molekülünün ikincil ve üçüncül yapısı hakkındaki bilgiyi kullanılır. Bu yöntemler iki ve daha çok dizi için uygulanabilir ve tipik olarak lokal hizalamalar üretir. Ancak, yapısal bilgiye bağımlı oldukları için, sadece yapısı bilinen dizilerde işe yararlar. Gerek protein gerek RNA'da yapı, evrimsel olarak diziden daha çok korunur,[13] Evrimsel olarak çok uzaktan ilişkili olan, dizi kıyaslaması yoluyla benzerlikleri belirlenemeyecek derecede ıraksamış dizilerde yapısal hizalamalar daha güvenilir sonuç verir.

Homoloji-temelli protein yapı tahmini için yapılan hizalamaları değerlendirmede yapısal hizalamalar "altın standart" sayılır[14] Bunun nedeni, sadece dizi bilgisine dayanmak yerine yapısal benzerlik gösteren bölgeleri kasten hizalamalarıdır. Ancak, tamamen yapısal hizalamalar tabii ki yapı tahmininde kullanılamaz çünkü sorgu kümesindeki en az bir dizi, modellenmesi amaçlanan hedef dizidir ve onun yapısı bilinmemektedir. Bir hedef ve bir kalıp dizinin yapısal hizalamasında, hedef proteinin yüksek doğruluklu modellerinin bu tür yöntemlerle elde edilebileceği gösterilmiştir.[14]

DALI

DALI yöntemi (İngilizce distance matrix alignment teriminden kısaltılmıştır), sorgu dizisindeki ardışık heksapeptitlerin temas benzerliklerine dayanarak elde edilen yapısal bir hizalama yöntemidir.[15] Bu yöntemle ikili veya çoklu hizalamalar üretebilir ve sorgu dizisinin Protein Data Bank'taki yapısal komşularını tespit edebilir. FSSP yapısal hizalama veri tabanını oluşturmakta kullanılmıştır. DALI Web sunucusuna EBI DALI'den ulaşılabilir, FSSP ise The Dali Database'de bulunmaktadır.

SSAP

SSAP (sequential structure alignment program, sıralı yapı hizalama programı), dinamik programlama ile çalışan bir yapısal hizalama yöntemidir, yapı uzayında atomdan atoma vektörleri kıyaslama noktaları olarak değerlendirir. İlk tarif edilişinden beri bu yöntem geliştirilerek hem ikili hem de çoklu hizalamaları kapsamaktadır.[16]. SSAP kullanılarak CATH (Class, Architecture, Topology, Homology, sınıf mimarî, topoloji homoloji) adlı, protein katlamalarının hiyerarşik bir veritabanı kurulmuştur.[17] CATH veritabanına CATH Protein Structure Classification sitesinden erişilebilir.

Kombinatoryal uzatma

Yapısal hizalama için kombinatoryal uzatma yöntemi, karşılaştırılan iki proteinin kısa parçaları için lokal geometriye dayalı ikili yapısal hizalamalar yapar, sonra bu parçaları birleştirerek daha büyük bir hizalama yapar.[18] Katı-gövde (rigid body) karekök ortalama uzaklık, kalıntı uzaklıkları, lokal ikincil yapı ve çevresel özellikler (kalıntı komşu hidrofobisitesi gibi) kullanılarak "hizalanmış parça ikilileri" denen lokal hizalamalar üretilir. Bunlar kullanılarak, belli tanımlanmış eşik kıstasları dahilinde tüm olasıl yapısal hizalamaları temsil eden bir benzerlik matrisi inşa edilir. Büyüyen birer dizi parçası eklenerek hizalama büyütülür. Bu işlem sırasında, matris aracılığıyla, bir protein yapı hâlinden diğerine giden bir yol çizilir; optimal yol, kombinatoryal uzatma hizalamasını tanımlar. Bu yöntemi uygulayan bir Web sunucusu ve Protein Data Bank'taki yapılar için ikili hizalamalar veritabanı Combinatorial Extension sitesinde bulunmaktadır.

Filogenetik analiz

(Ana|Berimsel filogenetik) Filogenetik ve dizi hizalaması birbiriyle yakından ilişkili sahalardır çünkü ikisi de dizi yakınlığı belirlemesi yapar. Filogenetik sahası, filogenetik ağaçların inşası ve yorumlamasında dizi hizalamasından yararlanır. Filogenetik ağaçlar, evrimsel olarak ıraksamış türlerin genomlarında bulunan homolog genlerdeki evrimsel ilişkiyi sınıflandırmakta kullanılır. Bir sorgu kümesindeki dizilerin birbirlerinden farklılığı, bu dizilerin birbirlerine olan evrimsel uzaklığı ile nitel olarak ilişkilidir. Basit şekilde ifade edilecek olursa, yüksek derecede dizi aynılığı, söz konusu dizilerin nispeten yakın zamanda bir en yakın ortak atası olabileceğini ima eder, buna karşın düşük derecede aynılık, evrimsel ıraksamanın daha eskilere dayandığı olasılığına karşılık gelir. Bu ilkenin dayalı olduğu "moleküler saat" hipotezine göre dizilerden meydana gelen soylarda mutasyon ve seleksiyon etkisinin değişmediği varsayılır. Yaklaşık sabit bir evrimsel değişim hızına dayanarak yapılacak bir ekstrapolasyon sayesinde, iki genin ilk defa birbirinden ne zaman farklılaştığının hesaplanabilir. Dolayısıyla, organizmalar veya türler arasında DNA tamiri yeteneği bakımından farklılık olabileceğini, veya dizilerde belli bölgelerin işlevsel nedenlerle korunabileceğini hesaba katmaz. Ayrıca, moleküler saat hipotezinin en basit versiyonunda, protein kodlayıcı bölgelerde proteinin amino asit dizisini değiştiren ve değiştirmeyen DNA mutasyonlarının korunma olasılıkları arasında bir fark olabileceği de hesaba katılmaz. Daha hassas istatistik yöntemler bir filogenetik ağacın her dalı için evrimleşme hızının farklı olmasına izin verir, bu sayede gen soylarının birleştiği zamanın daha doğru kestirilmesine olanak verir.

İlerleyici çoklu hizalama teknikleri zorunlu olarak bir filogenetik ağaç üretir, çünkü büyüyün hizalamaya ekledikleri dizilerin sırası, evrimsel yakınlık derecesine bağlıdır. Çoklu dizi hizalamalarını ve filogenetik ağaçları oluşturan diğer yöntemler önce tüm olasıl ağaçlara bir skor verir, sonra en yüksek skora sahip ağaçtan bir çoklu dizi hizalaması hesaplar. Filogenetik ağaç inşasında yaygın olarak kullanılan yöntemler başlıca höristiktir çünkü optimal ağacın seçilmesi, optimal çoklu dizi hizalamasının seçilmesi gibi, NP-zordur.[19]

Anlamlılık tayini

Dizi hizalaması biyoenformatikte dizi benzerliğini tespit etmeye, filogenetik ağaç üretmeye ve protein yapıları için homoloji modelleri geliştirmeye yarar. Ancak, dizi hizalamalarının biyolojik anlamı her zaman açık değildir. Hizalamaların, ortak atadan inmiş diziler arasındaki evrimsel farklılığı yansıttığı varsayılır. Fakat, evrimsel olarak ilişkisiz olup benzer işlev gösteren ve bu yüzden benzer yapıya sahip proteinlerin yakınsak evrim sonucu dizi benzerliği göstermeleri mümkündür.

BLAST gibi veritabanı aramalarında, istatistik yöntemler kullanılarak, diziler arasında belli bir hizalamanın şans eseri olma olasılığı, veritabanının büyüklüğü ve bileşimine dayanarak hesaplanabilir. Arama uzayına bağlı olarak olasılık değerleri önemli derecede farkedebilir. Eğer veritabanındaki diziler sadece sorgu dizisin organizmasına ait dizilerden oluşuyorsa, belli bir hizalamanın şans eseri olma olasılığı özellikle artar. Veritabanında veya sorgu dizisinde tekrarlı dizilerin varlığı hem arama sonuçlarını hem de istatistik anlamlılık tayinini çarpıtabilir. BLAST otomatik olarak sorgu dizisindeki tekrarlı dizileri filtreler, böylece istatistik artifakt sonucu olan bulguları elimine eder.

Boşluklu dizi hizalamalarının istatistik anlamlılığını kestiren istatistik yöntemler literatürde mevcuttur.[20][21]

İnanılırlık tayini

İstatistik anlamlılık, belli kaliteye sahip bir hizalamanın şans eseri elde edilme olasılığını gösterir ama sorgu dizisinin belli bir hizalamasının diğer hizalamalardan ne derece daha iyi olduğunu belirtmez. Hizalanma inanılırlığının ölçütleri, belli bir dizi ikilisi için en yüksek skorlu hizalamalarının ne derece birbirine eşdeğer olduğunu gösterir. Boşluklu dizi hizalamaları için istatistik inanılırlık değerlendirme yöntemleri literatürde mevcuttur.[22]

Skor fonksiyonları

Bilinen diziler hakkında biyolojik veya istatistik gözlemleri yansıtan bir skor fonksiyonunun seçimi, iyi hizalamalar elde edilmesinde çok önemlidir. Protein dizileri genelde substitusyon matrisleri kullanılarak yapılır, bu matrisler belli karakter substitusyonlarının olma olasılıklarını yansıtır. PAM matrisi (Point accepted mutation, noktasal olarak kabul edilmiş mutasyon) olarak adlandırılan bir grup matris, belli amino asit mutasyonlarının olma hızları ve olasılıklarını içerir (bu matrisler Margaret Dayhoff tarafından tanımlanmış olduğu için bazen "Dayhoff matrisleri" olarak da adlandrılır). Sık kullanılan başka bir grup matris ise BLOSUM (Blocks Substitution Matrix blok substitusyon matrisi) olarak adlandırılır, bunlar empirik olarak gözlemlenmiş substitusyon olasılıklarını kodlar. Her iki tip matrislerin varyantları, farklı düzeylerde ıraksama göstermiş dizilerin tayininde kullanılır. Böylece, BLAST veya FASTA kullanıcıları aramalarını sadece yakın ilişkili uyuşmalara kendilerini sınırlayabilir, veya arzu ederlerse daha uzak ilişkili dizileri de bulabilmeleri mümkün olur. Boşluk cezaları hizalamaya bir boşluk katılmasına etki eder. Bu boşluk ceza skoru, evrimsel anlamda bir insersiyon veya delesyon mutasyonunun olma hızı ile orantılı olmalıdır. Elde edilen hizalamaların kalitesi skor fonksiyonunun kalitesine bağlıdır.

Aynı hizalamayı farklı skor matrisleri ve/veya boşluk cezaları ile tekrarlayıp sonuçları karşılaştırmak çok yararlı olabilir. Hizalama parametrelerindeki varyasyonlara dayanıklılık gösteren hizalama bölgeleri tespit edilerek, sonucun zayıf olduğu veya tek olmadığı bölgeler belirlenebilir.

Diğer biyolojik uygulamalar

Dizilenmiş RNA, örneğin "ifade edilmiş dizi etiketleri (expressed sequence tags) ve tam-uzunluklu mRNAlar, dizilenmiş bir genom ile hizalanarak nerede genlerin bulunduğu ve alternatif uçbirleştirme yerleri hakkında bilgi edinilebilir.[23] and RNA editing.[24] Dizi hizalaması ayrıca genom birleştirme (genome assembly) sürecinin parçasıdır. Dizilenen parçalar hizalanarak örtüşme yerleri bulunur, böylece kontig adı verilen uzun diziler oluşturulur.[25] Bir diğer uygulama, SNP (single nucleotide polymorphism tekil nükleotit polimorfizmi) analizidir, burada farklı kişilera ait diziler hizalanarak toplulukta farklılık gösteren tek nükleotitler bulunur.[26]

Biyolojik olmayan uygulamalar

Biyolojik dizi hizalamasında kullanılan yöntemler başka sahalarda da uygulamaları olmuştur, özellikle doğal dil işlemlemesi (natural language processing) ve sosyal bilimlerde.[27] Doğal dil üretme algoritmaları tarafından sözcük seçimi, biyoenformatikte geliştirilmiş çoklu dizi hizalama yöntemleri kullanmaktadır.[28] Tarihsel ve karşılaştırmali dilbilim sahalarında, dilbilimcilerin dilleri oluşturmak için kullandıkları karşılaştırma yöntemi, dizi hizalaması ile otomatize edilmiştir.[29] İşletme ve pazarlama araştırmacıları zaman içinde bir dizi satın alma olayını analiz etmek için çoklu dizi hizalama yöntemlerini kullanmıştır.[30]

Yazılım

Algoritma ve hizalama tipine göre kategorize edilmiş yazılımları daha geniş bir listesi dizi hizalama yazılımı maddesinde verilmiştir. Genel dizi hizalama problemlerinde yaygın kullanılan araçlar arasında ClustalW ve T-coffee, veritabanı araması için de BLAST ve FASTA3x sayılabilir.

Hizalama algoritma ve yazılımlarını karşılaştırmak için BAliBASE adlı sistem test programı (benchmark) referans çoklu dizi hizalamaları mevcuttur.[31] Bu veri grubu yapısal hizalamalardan oluşmaktadır, sadece diziye dayalı yöntemler için bunun bir standart oluşturduğu düşünülebilir. Çoğu hizalama yönteminin göreceli performansı, sıklıkla görülen hizalama problemleri için belirlenmiş ve sonuçlar BAliBASE sitesinde yayımlanmıştır.[32] Farklı hizalama araçları için BAliBASE skorlarının kapsamlı bir listesi STRAP sitesinde hesaplanabilir.

Kaynakça

  1. 1 2 3 Mount DM. (2004). Bioinformatics: Sequence and Genome Analysis (2 bas.). Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY.. ISBN 0-87969-608-7.
  2. ↑ Ng PC, Henikoff S. Predicting deleterious amino acid substitutions. Genome Res. 2001 May;11(5):863-74.
  3. ↑ Schneider TD, Stephens RM (1990). "Sequence logos: a new way to display consensus sequences". Nucleic Acids Res 18: 6097–6100. DOI:10.1093/nar/18.20.6097. PMC 332411. PMID 2172928. http://nar.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=2172928.
  4. ↑ Brudno M, Malde S, Poliakov A, Do CB, Couronne O, Dubchak I, Batzoglou S (2003). "Glocal alignment: finding rearrangements during alignment". Bioinformatics 19 Suppl 1: i54–62. DOI:10.1093/bioinformatics/btg1005. PMID 12855437. http://bioinformatics.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=12855437.
  5. ↑ Wang L, Jiang T. (1994). "On the complexity of multiple sequence alignment". J Comput Biol 1: 337–48. PMID 8790475.
  6. ↑ Lipman DJ, Altschul SF, Kececioglu JD (1989). "A tool for multiple sequence alignment". Proc Natl Acad Sci USA 86: 4412–5. DOI:10.1073/pnas.86.12.4412. PMID 2734293. http://www.pnas.org/cgi/pmidlookup?view=long&pmid=2734293.
  7. ↑ Higgins DG, Sharp PM (1988). "CLUSTAL: a package for performing multiple sequence alignment on a microcomputer". Gene 73 (1): 237–44. DOI:10.1016/0378-1119(88)90330-7. PMID 3243435. http://linkinghub.elsevier.com/retrieve/pii/0378-1119(88)90330-7.
  8. ↑ Thompson JD, Higgins DG, Gibson TJ. (1994). "CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice". Nucleic Acids Res 22: 4673–80. DOI:10.1093/nar/22.22.4673. PMC 308517. PMID 7984417. http://nar.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=7984417.
  9. ↑ Chenna R, Sugawara H, Koike T, Lopez R, Gibson TJ, Higgins DG, Thompson JD. (2003). "Multiple sequence alignment with the Clustal series of programs". Nucleic Acids Res 31: 3497–500. DOI:10.1093/nar/gkg500. PMID 12824352. http://nar.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=12824352.
  10. ↑ Notredame C, Higgins DG, Heringa J. (2000). "T-Coffee: A novel method for fast and accurate multiple sequence alignment". J Mol Biol 302 (1): 205–17. DOI:10.1006/jmbi.2000.4042. PMID 10964570. http://linkinghub.elsevier.com/retrieve/pii/S0022-2836(00)94042-7.
  11. ↑ Hirosawa M, Totoki Y, Hoshida M, Ishikawa M. (1995). "Comprehensive study on iterative algorithms of multiple sequence alignment". Comput Appl Biosci 11: 13–8. DOI:10.1093/bioinformatics/11.1.13. PMID 7796270. http://bioinformatics.oxfordjournals.org/cgi/content/abstract/11/1/13.
  12. ↑ Karplus K, Barrett C, Hughey R. (1998). "Hidden Markov models for detecting remote protein homologies". Bioinformatics 14 (10): 846–856. DOI:10.1093/bioinformatics/14.10.846. PMID 9927713. http://bioinformatics.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=9927713.
  13. ↑ Chothia C, Lesk AM. (April 1986). "The relation between the divergence of sequence and structure in proteins". EMBO J 5 (4): 823–6. PMC 1166865. PMID 3709526. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1166865.
  14. 1 2 Zhang Y, Skolnick J. (2005). "The protein structure prediction problem could be solved using the current PDB library". Proc Natl Acad Sci USA 102: 1029–34. DOI:10.1073/pnas.0407152101. PMID 15653774. http://www.pnas.org/cgi/pmidlookup?view=long&pmid=15653774.
  15. ↑ Holm L, Sander C (1996). "Mapping the protein universe". Science 273: 595–603. DOI:10.1126/science.273.5275.595. PMID 8662544. http://www.sciencemag.org/cgi/pmidlookup?view=long&pmid=8662544.
  16. ↑ Taylor WR, Flores TP, Orengo CA. (1994). "Multiple protein structure alignment". Protein Sci 3: 1858–70. DOI:10.1002/pro.5560031025. PMID 7849601. http://www.proteinscience.org/cgi/pmidlookup?view=long&pmid=7849601.
  17. ↑ Orengo CA, Michie AD, Jones S, Jones DT, Swindells MB, Thornton JM (1997). "CATH--a hierarchic classification of protein domain structures". Structure 5: 1093–108. DOI:10.1016/S0969-2126(97)00260-8. PMID 9309224.
  18. ↑ Shindyalov IN, Bourne PE. (1998). "Protein structure alignment by incremental combinatorial extension (CE) of the optimal path". Protein Eng 11: 739–47. DOI:10.1093/protein/11.9.739. PMID 9796821. http://peds.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=9796821.
  19. ↑ Felsenstein J. (2004). Inferring Phylogenies. Sinauer Associates: Sunderland, MA. ISBN 0-87893-177-5.
  20. ↑ Newberg LA (2008). "Significance of gapped sequence alignments". J Comput Biolo 15: 1187–1194. DOI:10.1089/cmb.2008.0125. PMID 18973434.
  21. ↑ Eddy SR (2008). "A probabilistic model of local sequence alignment that simplifies statistical significance estimation". PLoS Comput Biol 4: e1000069. DOI:10.1371/journal.pcbi.1000069. PMID 18516236.
  22. ↑ Newberg LA, Lawrence CE (2009). "Exact Calculation of Distributions on Integers, with Application to Sequence Alignment". J Comput Biolo 16 (1): 1–18. DOI:10.1089/cmb.2008.0137. PMID 19119992.
  23. ↑ Kim N, Lee C (2008). "Bioinformatics detection of alternative splicing". Methods Mol. Biol. 452: 179–97. DOI:10.1007/978-1-60327-159-2_9. PMID 18566765.
  24. ↑ Li JB, Levanon EY, Yoon JK, et al. (May 2009). "Genome-wide identification of human RNA editing sites by parallel DNA capturing and sequencing". Science 324 (5931): 1210–3. DOI:10.1126/science.1170995. PMID 19478186.
  25. ↑ Blazewicz J, Bryja M, Figlerowicz M, et al. (June 2009). "Whole genome assembly from 454 sequencing output via modified DNA graph concept". Comput Biol Chem 33 (3): 224–30. DOI:10.1016/j.compbiolchem.2009.04.005. PMID 19477687.
  26. ↑ Duran C, Appleby N, Vardy M, Imelfort M, Edwards D, Batley J (May 2009). "Single nucleotide polymorphism discovery in barley using autoSNPdb". Plant Biotechnol. J. 7 (4): 326–33. DOI:10.1111/j.1467-7652.2009.00407.x. PMID 19386041.
  27. ↑ Abbott A., Tsay A. (2000). "Sequence Analysis and Optimal Matching Methods in Sociology, Review and Prospect". Sociological Methods and Research 29: 3–33. DOI:10.1177/0049124100029001001.
  28. ↑ Barzilay R, Lee L. (2002). "Bootstrapping Lexical Choice via Multiple-Sequence Alignment" (PDF). Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP) 10: 164–171. DOI:10.3115/1118693.1118715. http://www.cs.cornell.edu/home/llee/papers/gen-msa.pdf.
  29. ↑ Kondrak, Grzegorz (2002). "Algorithms for Language Reconstruction" (PDF). University of Toronto, Ontario. 26 Mart 2009 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20090326085405/http://www.cs.ualberta.ca/~kondrak/papers/thesis.pdf. Erişim tarihi: 2007-01-21.
  30. ↑ Prinzie A., D. Van den Poel (2006). "Incorporating sequential information into traditional classification models by using an element/position-sensitive SAM". Decision Support Systems 42 (2): 508–526. DOI:10.1016/j.dss.2005.02.004. http://econpapers.repec.org/paper/rugrugwps/05_2F292.htm. See also Prinzie and Van den Poel's paper Prinzie, A (2007). "Predicting home-appliance acquisition sequences: Markov/Markov for Discrimination and survival analysis for modeling sequential information in NPTB models". Decision Support Systems 44 (1): 28–45. DOI:10.1016/j.dss.2007.02.008. http://econpapers.repec.org/paper/rugrugwps/07_2F442.htm.
  31. ↑ Thompson JD, Plewniak F, Poch O (1999). "BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs". Bioinformatics 15: 87–8. DOI:10.1093/bioinformatics/15.1.87. PMID 10068696. http://bioinformatics.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=10068696.
  32. ↑ Thompson JD, Plewniak F, Poch O. (1999). "A comprehensive comparison of multiple sequence alignment programs". Nucleic Acids Res 27: 2682–90. DOI:10.1093/nar/27.13.2682. PMID 10373585. http://nar.oxfordjournals.org/cgi/pmidlookup?view=long&pmid=10373585.
This article is issued from Vikipedi - version of the 9/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.