J-değişmezi

karmaşık düzlem içinde Klein'ın j-değişmezi

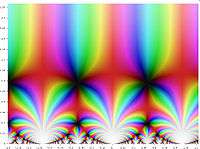
Matematikte, Klein'ın j-değişmezi, bir  τ karmaşık değişkenin bir foksiyonu olarak sunulur,bir ${\displaystyle SL(2,\mathbb {Z} )}$ için karmaşık sayıların üst yarı-düzleminde sıfır ağırlığın bir modüler fonksiyonu olarak tanımlanır.Eşsiz böyle bir işlevi olan zirvede basit bir kutuptan uzakta holomorfik olacak şekilde ${\displaystyle j\left(e^{{\frac {2}{3}}\pi i}\right)=0}$ ve ${\displaystyle j(i)=1728}$.${\displaystyle j}$ in rasyonel fonksiyonu modülerdir, ve aslında tüm modüler fonksiyonları verir. Klasik olarak,j-değişmezi eliptik eğrilerin bir parametrizasyonu olarak ${\displaystyle \mathbb {C} }$ üzerinde incelendi, ama onun ayrıca Monster grubu'nun simetrilerine sürpriz bağlantıları var (bu bağlantı canavarlaşmış ayışığı'na kaynaktır).

Tanımlar

J-değişmez (aşağıda ${\displaystyle g_{2},g_{3}}$ bkz.), bazı sonsuz toplamları bakımından tamamen tanımlanabilir iken, bu eliptik eğrilerin eşyapı sınıfları dikkate alınarak motive edilebilir.Her ${\displaystyle E}$ eliptik eğri ${\displaystyle \mathbb {C} }$ üzerinde bir karmaşık tordur, ve böylece bir rank 2 kafesi ile eşlenebilir; yani,${\displaystyle \mathbb {C} }$nin iki boyutlu kafesidir. Bu veri ile kafes içinde her paralelkenarın karşı köşesi belirlenir. Bu, karmaşık sayılar kafesle çarpılarak çıkan kafes döndürme ve ölçeklemeye karşılık gelir, eliptik eğrinin izomorfizm sınıfı korunur ve böylece biz 1 tarafından oluşturulan kafes düşünebiliriz${\displaystyle \tau \in \mathbb {H} }$ (burada ${\displaystyle \mathbb {H} }$ üstyarı-düzlemdir). Tersine, eğer şöyle tanımlarsak

${\displaystyle g_{2}=60\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-4},\qquad g_{3}=140\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-6}}$

eliptik eğriye bu kafes karşı geliyorsa ${\displaystyle \mathbb {C} }$ üzerine ${\displaystyle y^{2}=4x^{3}-g_{2}X-g_{3}}$ ile Weierstrass eliptik fonksiyonları üzerinden tanımlanır,j-değişmezi ise

${\displaystyle j(\tau )=1728{g_{2}^{3} \over \Delta }}$

olarak tanımlanır

burada modular diskriminant ${\displaystyle \Delta }$

${\displaystyle \Delta =g_{2}^{3}-27g_{3}^{2}}$ dır

${\displaystyle \Delta }$ olarak gösterilebilen oniki ağırlığının bir modular formudur ve dört ağırlığının bir ${\displaystyle g_{2}}$dir, böylece onun üçüncü kuvveti ayrıca oniki ağırlığınındır. Böylece bölüm, ve bunun için ${\displaystyle j}$ ağırlık sıfırın bir modüler fonksiyonudur, özel olarak bir meromorfik fonksiyon ${\displaystyle \mathbb {H} \rightarrow \mathbb {C} }$ ifadesi ${\displaystyle \operatorname {SL} (2,\mathbb {Z} )}$nin hareketi altında değişmezdir.Aşağıda açıklandığı gibi,, ${\displaystyle j}$ örtendir, bunun anlamı o verilen ${\displaystyle \mathbb {C} }$ üzerinde eliptik eğrilerin bir eşyapı sınıfları arasındaki tanımlansın ve karmaşık sayılar.

Temel bölge

Üst yarı düzlem üzerinde hareket eden modüler grubunun temel etki alanı.

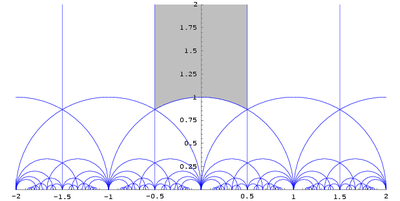
İki dönüşüm τ → τ + 1 ve τ → τ⁻¹ birlikte bir grup üretir adına modüler grup denir, bunu biz ${\displaystyle PSL_{2}(\mathbb {Z} )}$ ile izdüşümsel özel doğrusal grup olarak olarak tespit edebiliriz.Bu gruba ait olan dönüşümün uygun bir seçimi ile, τ → (aτ + b)/(cτ + d),ad − bc = 1 ile, Biz j için aynı değeri veren ve temel bölgesinde yer alan,bir değere τ'yi indirgeyebiliriz,τ koşulları tatmin edici değerlerden oluşur ki;

${\displaystyle {\begin{aligned}|\tau |&\geq 1\\-{\frac {1}{2}}&<{\mathfrak {R}}(\tau )\leq {\frac {1}{2}}\\-{\frac {1}{2}}&<{\mathfrak {R}}(\tau )<0\Rightarrow |\tau |>1\end{aligned}}}$

Bu bölgeye sınırlı fonksiyonu j(τ) yine ${\displaystyle \mathbb {C} }$ tam bir kez karmaşık sayılar her değer alır.Başka bir değişle, her ${\displaystyle c\in \mathbb {C} }$ için, burada τ temel bölge içinde bir eşsizdir ve c=j(τ).Böylece,j tüm karmaşık düzleme temel bölgeyi haritalama özelliğine sahiptir.

Riemann yüzeyi olarak, temel bölge cins 0 var, ve her (seviye bir) modüler fonksiyonj içinde bir rasyonel fonksiyondur; ve, tersine, j içindeki her rasyonel fonksiyon bir modüler fonksiyondur.Diğer bir değişle modüler fonksiyonların alanı ${\displaystyle \mathbb {C} (j)}$dir.

Sınıf alan teorisi ve j

j-değişmezi çok dikkat çekici özelliklere sahiptir. Bunlardan biri, τ tekil modülünün herhangi biri ise, pozitif sanal bir parçası olan sanal kuadratik alanın herhangi bir öğesi (böylece j tanımlandığı gibidir), daha sonra ${\displaystyle j(\tau )}$ bir cebirsel tamsayı olmasıdır.^[1] Alan uzantısı

${\displaystyle \mathbb {Q} [j(\tau ),\tau ]/\mathbb {Q} (\tau )}$

bu abelyen Galois grup anlamıyla abelyendir.Biz karmaşık düzlem içinde bir kafes 1 ve τ ile tanımlarız, ve ${\displaystyle \mathbb {Q} (\tau )}$ alanının ögelerinin hepsinin görünmesi kolaydır bu bir halka ile birimlerin çarpma formu altında diğer kafes noktasına gönderir ve bir düzen denir. Aynı sırada benzer biçimde ilişkili 1 ve τ' jeneratöri ile diğer kafesler ${\displaystyle \mathbb {Q} (\tau )}$ üzerinde ${\displaystyle j(\tau )}$ nun ${\displaystyle j(\tau ')}$ cebirsel eşleniğini tanımlar. ${\displaystyle \mathbb {Q} (\tau )}$ nun dahil altında eşsiz maksimal sırası ${\displaystyle \mathbb {Q} (\tau )}$ cebirsel tamsayıların halkasıdır,ve τ'nin ilişkili sıra olarak sahip olduğu değerleri ${\displaystyle \mathbb {Q} (\tau )}$'nun dallanmamış uzatmalarına yol açabilir . Bu klasik sonuçlar karmaşık çarpımın teorisi için başlangıç noktasıdır.

Aşkın özellikler

1937 de Theodor Schneider anılan sonucu kanıtlamıştırki eğer ${\displaystyle \tau }$ üst yarı düzlem j(${\displaystyle \tau }$) içinde bir kuadratik irrasyonel sayı ise bir cebrik tamsayıdır.Buna ek olarak kanıtlanmıştırki eğer ${\displaystyle \tau }$ bir cebirsel sayı ama sanal kuadratik değil ise j(${\displaystyle \tau }$) aşkındır. j fonksiyonunun numaralı diğer aşkın özellikleri var.Kurt Mahler sanısının bu özel aşkın sonuçları Mahler sanısı olarak sıklıkla ona ithaf edilir,gerçi sonuçlarının bir doğal sonucu olarak Yu tarafından kanıtlanmıştı. V. Nesternko ve Patrice Phillipon 1990 yılında. Mahler sanısı şu idi ki eğer${\displaystyle \tau }$ üst yarı düzlemde ise exp(2πi${\displaystyle \tau }$) ve j(${\displaystyle \tau }$) ikisi birden asla eşzamanlı cebri değildir.Güçlü sonuçlar artık bilinmektedir, örneğin eğer exp(2πi${\displaystyle \tau }$) cebirsel ise aşağıdaki üç sayı cebrik bağımsızdır , ve böylece aşkın:

${\displaystyle j(\tau ),{\frac {j^{\prime }(\tau )}{\pi }},{\frac {j^{\prime \prime }(\tau )}{\pi ^{2}}}}$

q-açılımı ve ayışığı

jnin dikkat çekici özellikleri ile q-açılımı yapmak zorundadır (Fourier serisi açılımıdır. q= exp(2πiτ))nun terimleri içinde bir Laurent serisi olarak yazılır ,bunun başlaması:

${\displaystyle j(\tau )={1 \over q}+744+196884q+21493760q^{2}[phone]q^{3}[phone]q^{4}+\cdots }$

Unutmadan j basit bir kutup zirve vardı, böylece bu q-açılımıdır aşağıdaki q⁻¹ terimleri yoktur.

Tüm katsayıları tamsayıdır, bunun birkaç yaklaşık tamsayılar içinde sonuçları , özellikle Ramanujan'ın sabiti: ${\displaystyle e^{\pi {\sqrt {163}}}\approx 640320^{3}+744}$.

Ayışığı

Daha dikkat çekici,q pozitif üslerin için Fourier katsayıları canavar grup ay ışığı modül denilen bir sonsuz boyutlu dereceli cebir gösterim kısmının boyutları - özellikle ${\displaystyle q^{n}}$ katsayısı- ay ışığı modülünün parçası derece n in boyutudur.ilk örneği Griess cebiri 196.884 boyuta sahiptir${\displaystyle 196884q^{1}.}$ terimine karşılık bu şaşırtıcı gözlem ay ışığı teorisi için başlangıç ​​noktası oldu.

J.H. Conway ve Simon P. Nortonun cins-sıfır modüler fonksiyonlara bakması ayışığı varsayım çalışmasına yol açtı . Formu için normalize ise

${\displaystyle q^{-1}+{O}(q)}$

ise Thompson yalnız burada şunu gösterdiki böyle fonksiyonların sonlu bir sayısı (bazı sonlu seviyelerin)sonludur, ve Cummins sonra göstermiştir ki orada tam olarak bunların sayısı 6.486 dır,bunların 616'sı integral katsayılarıdır.^[2]

Diğer ifadeler

Bizde

${\displaystyle j(\tau )={\frac {256(1-x)^{3}}{x^{2}}}}$

var burada ${\displaystyle x=\lambda (1-\lambda )}$ ve ${\displaystyle \lambda }$ modüler lambda fonksiyonudur.jnin değeri değişmemiş olduğundan λ Çapraz oranının herhangi altı değerinin yerinedir :^[3]

${\displaystyle \left\lbrace {\lambda ,{\frac {1}{1-\lambda }},{\frac {\lambda -1}{\lambda }},{\frac {1}{\lambda }},{\frac {\lambda }{\lambda -1}},1-\lambda }\right\rbrace }$

jnin dal noktası {0,1,∞}de'dir, böylece j bir Belyi fonksiyonudur.^[4]

Teta fonksiyonunun terimleri içindeki uzantılar

${\displaystyle g_{2}(\tau )={2\pi ^{4} \over 3}\left[\vartheta (0;\tau )^{8}+\vartheta _{01}(0;\tau )^{8}+\vartheta _{10}(0;\tau )^{8}\right]}$

${\displaystyle \Delta (\tau )=16\pi ^{12}\left[\vartheta (0;\tau )\vartheta _{01}(0;\tau )\vartheta _{10}(0;\tau )\right]^{8}}$

Bu çok hızlı bir şekilde hesaplanabilir formu olan Jacobi'nin teta fonksiyonunun terimleri içinde ifade edilebilir

${\displaystyle j(\tau )=32{[\vartheta (0;\tau )^{8}+\vartheta _{01}(0;\tau )^{8}+\vartheta _{10}(0;\tau )^{8}]^{3} \over [\vartheta (0;\tau )\vartheta _{01}(0;\tau )\vartheta _{10}(0;\tau )]^{8}}}$

Cebrik tanım

Şimdiye kadar göz önünde olan j bir karmaşık değişkenin bir fonksiyonudur. Ancak, eliptik eğrilerin eşyapı sınıfları için bir değişmez olarak, bu tamamen cebirsel tanımlanabilir. Diyelimki

${\displaystyle y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}$

herhangi bir alan üzerinde bir düzlem eliptik eğri olmasıdır. ise şöyle tanımlayabiliriz

${\displaystyle b_{2}=a_{1}^{2}+4a_{2},\quad b_{4}=a_{1}a_{3}+2a_{4}}$

${\displaystyle b_{6}=a_{3}^{2}+4a_{6},\quad b_{8}=a_{1}^{2}a_{6}-a_{1}a_{3}a_{4}+a_{2}a_{3}^{2}+4a_{2}a_{6}-a_{4}^{2}}$

${\displaystyle c_{4}=b_{2}^{2}-24b_{4},\quad c_{6}=-b_{2}^{3}+36b_{2}b_{4}-216b_{6}}$

ve

${\displaystyle \Delta =-b_{2}^{2}b_{8}+9b_{2}b_{4}b_{6}-8b_{4}^{3}-27b_{6}^{2}}$

ikinci sentezleme eğrinin diskriminantıdır .

j-değişmezi eliptik eğri için

${\displaystyle j={c_{4}^{3} \over \Delta }}$

olarak şimdi tanımlanabilir

Eğri tanımlandığı alan üzerinde bir 2 ya da 3 farklı karakteristiğe sahip durumda ise, bu tanım aynı zamanda şu şekilde yazılabilir

${\displaystyle j=1728{c_{4}^{3} \over c_{4}^{3}-c_{6}^{2}}}$

Pi formülü

Chudnovsky kardeşler 1987'de buldu,

${\displaystyle {\frac {1}{\pi }}={\frac {12}{640320^{3/2}}}\sum _{k=0}^{\infty }{\frac {(6k)!(163\cdot 3344418k+13591409)}{(3k)!(k!)^{3}(-640320)^{3k}}}}$

ve aslında ${\displaystyle j{\big (}{\tfrac {1+{\sqrt {-163}}}{2}}{\big )}=-640320^{3}}$ kullanılır. Benzer formül için,Ramanujan–Sato serisine bakınız.

Ters ve özel değerler

j-değişmezinin ters fonksiyon hipergeometrik fonksiyon ${\displaystyle {}_{2}F_{1}}$ in terimleri içinde ifade edilebilir(ayrıca bak Picard–Fuchs denklemi makalesi). açıkça,${\displaystyle \tau }$ için çözümü denklemi içinde,

${\displaystyle j(\tau )=N}$

ise N biliniyor,diyelimki ${\displaystyle \alpha }$herhangi kök olsun,

${\displaystyle 4\alpha (1-\alpha )={\frac {1728}{N}}}$

ise,

${\displaystyle \tau =i{\frac {\,_{2}F_{1}{\big (}{\tfrac {1}{6}},{\tfrac {5}{6}},1,1-\alpha {\big )}}{\,_{2}F_{1}{\big (}{\tfrac {1}{6}},{\tfrac {5}{6}},1,\alpha {\big )}}}}$

τ bir kök verir, ve diğer verilen 1/τ, ama oysa ${\displaystyle j(\tau )=j(1/\tau )}$, ise o bir fark yapmaz bu ${\displaystyle \alpha }$ seçimdir. Alternatif olarak, olarak hatırladığım,

${\displaystyle j(\tau )={\frac {256(1-x)^{3}}{x^{2}}}}$

burada ${\displaystyle x=\lambda (1-\lambda )}$ ve ${\displaystyle \lambda }$ modüler lambda fonksiyondur.Bir bilinmeyen olarak, bir can find ${\displaystyle \lambda }$ by solving the cubic in x içinde, ise kuadratiktir. İse,

${\displaystyle \tau =i{\frac {\,_{2}F_{1}{\big (}{\tfrac {1}{2}},{\tfrac {1}{2}},1,1-\lambda {\big )}}{\,_{2}F_{1}{\big (}{\tfrac {1}{2}},{\tfrac {1}{2}},1,\lambda {\big )}}}}$

${\displaystyle \lambda }$ nın altı herhangi değeri için Onların tersinme oranları sınırsız halde olsa bile eliptik fonksiyonların periyotları yüksek hassasiyetli hesaplamalar sağlayan etkinleştirme yoluyla uygulamalarla son derece alakalıdır.Bununla ilgili bir sonuç büyüklükler sanal eksenin noktalarında j nin değerlerinin ikinci dereceden kökleri ile ifade edilebilir olduğundan 2'nin kuvvetleridir (böylece pusula ve cetvel inşaatlarına izin ). Bir ikinci sonuç dolayısıyla seviye 2 nin pek belirgin modüler denklemi kübiktir.

${\displaystyle {\frac {1}{2}}\left(1+i{\sqrt {3}}\right)}$ de temel domenin j-değişmezi "köşede" kaybolur.Burada birkaç özel değerler (bunun yalnızca ilk dördü iyi biliniyor; aşağıdakiler içinde, j anlamı J/1728 boyunca):

${\displaystyle {\begin{aligned}j\left(i\right)&=j\left({\tfrac {1+i}{2}}\right)=1\\j\left({\sqrt {2}}i\right)&=\left({\tfrac {5}{3}}\right)^{3}\\j\left(2i\right)&=\left({\tfrac {11}{2}}\right)^{3}\\j\left(2{\sqrt {2}}i\right)&=\left({\tfrac {5}{6}}\left[19+13{\sqrt {2}}\right]\right)^{3}\\j\left(4i\right)&=\left({\tfrac {1}{4}}\left[724+513{\sqrt {2}}\right]\right)^{3}\\j\left({\tfrac {1+2i}{2}}\right)&=\left({\tfrac {1}{4}}\left[724-513{\sqrt {2}}\right]\right)^{3}\\j\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&=\left({\tfrac {5}{6}}\left[19-13{\sqrt {2}}\right]\right)^{3}\\j\left(3i\right)&=\left(2+{\sqrt {3}}\right)^{2}\left({\tfrac {1}{3}}\left[21+20{\sqrt {3}}\right]\right)^{3}\\j\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\j\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {1}{7}}\left(40\left[651+142{\sqrt {21}}\right]\right)^{3}\\j\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\j\left({\sqrt {21}}i\right)&=\left({\tfrac {1}{2}}\left[5+3{\sqrt {3}}\right]\left[3+{\sqrt {7}}\right]\right)^{2}\left({\tfrac {1}{2}}\left[65+34{\sqrt {3}}+26{\sqrt {7}}+15{\sqrt {21}}\right]\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{1}}\right)&=\left({\tfrac {1}{2}}\left[10+7{\sqrt {2}}+4{\sqrt {5}}+3{\sqrt {10}}\right]\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{2}}\right)&=\left({\tfrac {1}{2}}\left[10+7{\sqrt {2}}-4{\sqrt {5}}-3{\sqrt {10}}\right]\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{5}}\right)&=\left({\tfrac {1}{2}}\left[10-7{\sqrt {2}}+4{\sqrt {5}}-3{\sqrt {10}}\right]\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\j\left({\tfrac {{\sqrt {30}}i}{10}}\right)&=\left({\tfrac {1}{2}}\left[10-7{\sqrt {2}}-4{\sqrt {5}}+3{\sqrt {10}}\right]\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\j({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\j(7i)&=\left(1+{\tfrac {9}{4}}{\sqrt {21+8{\sqrt {7}}}}\left(30+11{\sqrt {7}}+(6+{\sqrt {7}}){\sqrt {21+8{\sqrt {7}}}}\right)^{2}\right)^{3}\\j(8i)&=\left(1+{\tfrac {9}{4}}(1+{\sqrt {2}}){\sqrt {\sqrt {2}}}\left(123+104{\sqrt {\sqrt {2}}}+88{\sqrt {2}}+73{\sqrt {2}}{\sqrt {\sqrt {2}}}\right)^{2}\right)^{3}\\j\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left[9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right]^{2}\right)^{3}\\j\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left[22297077+9971556{\sqrt {5}}+(3571365+1597163{\sqrt {5}}){\sqrt {\tfrac {31+21{\sqrt {5}}}{2}}}\right]^{2}\right)^{3}\end{aligned}}}$

Kaynakça

1. Silverman, Joseph H. (1986). The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics. 106. Springer-Verlag. s. 339. ISBN 0-387-96203-4. Zbl 0585.14026. 
2. Cummins, C.J. (2004). "Congruence subgroups of groups commensurable with PSL(2,Z)$ of genus 0 and 1". Exp. Math. 13 (3): 361–382. ISSN 1058-6458. Zbl 1099.11022. 
3. Chandrasekharan, K. (1985), Elliptic Functions, Grundlehren der mathematischen Wissenschaften, 281, Springer-Verlag, ss. 110, ISBN 3-540-15295-4, Zbl 0575.33001 
4. Girondo, Ernesto; González-Diez, Gabino (2012), Introduction to compact Riemann surfaces and dessins d'enfants, London Mathematical Society Student Texts, 79, Cambridge: Cambridge University Press, ss. 267, ISBN 978-0-521-74022-7, Zbl 1253.30001 

• Apostol, Tom M. (1976), Modular functions and Dirichlet Series in Number Theory, Graduate Texts in Mathematics, 41, New York: Springer-Verlag, MR 0422157 . Provides a very readable introduction and various interesting identities.
  • Apostol, Tom M. (1990), Modular functions and Dirichlet Series in Number Theory (2nd bas.), ISBN 0-387-97127-0, MR 1027834 
• Berndt, Bruce C.; Chan, Heng Huat (1999), "Ramanujan and the modular j-invariant", Canadian Mathematical Bulletin 42 (4): 427–440, DOI:10.4153/CMB-1999-050-1, MR 1727340, http://www.journals.cms.math.ca/cgi-bin/vault/public/view/berndt7376/body/PDF/berndt7376.pdf . Provides a variety of interesting algebraic identities, including the inverse as a hypergeometric series.
• Cox, David A. (1989), Primes of the Form x^2 + ny^2: Fermat, Class Field Theory, and Complex Multiplication, New York: Wiley-Interscience Publication, John Wiley & Sons Inc., MR 1028322  Introduces the j-invariant and discusses the related class field theory.
• Conway, John Horton; Norton, Simon (1979), "Monstrous moonshine", Bulletin of the London Mathematical Society 11 (3): 308–339, DOI:10.1112/blms/11.3.308, MR 0554399 . Includes a list of the 175 genus-zero modular functions.
• Petersson, Hans (1932), "Über die Entwicklungskoeffizienten der automorphen Formen", Acta Mathematica 58 (1): 169–215, DOI:10.1007/BF02547776, MR 1555346 .
• Rademacher, Hans (1938), "The Fourier coefficients of the modular invariant j(τ)", American Journal of Mathematics (The Johns Hopkins University Press) 60 (2): 501–512, DOI:10.2307/2371313, JSTOR 2371313, MR 1507331 .
• Rankin, Robert A. (1977), Modular forms and functions, Cambridge: Cambridge University Press, ISBN 0-521-21212-X, MR 0498390 . Provides a short review in the context of modular forms.
• Schneider, Theodor (1937), "Arithmetische Untersuchungen elliptischer Integrale", Math. Annalen 113: 1–13, DOI:10.1007/BF01571618, MR 1513075 .