İntegral

f(x)'in a dan b'ye kadar olan integrali, y=f(x) fonsiyonunun a ile b arasındaki alanıdır.

Alan hesabı olarak integralin uygulanması

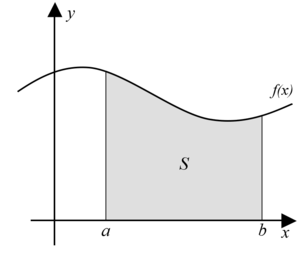
İntegral veya tümlev, bir fonksiyon eğrisinin altında kalan alan. Fonksiyonun, türevinin tersi olan bir fonksiyon elde edilmesini sağlar.

Tanım

Gottfried Wilhelm Leibniz

İntegral, verilen bir f(x) fonksiyonunu türev kabul eden F(x) fonksiyonunun bulunması olarak yapılabilir. F(x) fonksiyonuna f(x) fonksiyonunun integrali veya ilkeli denir. İntegral, Latince toplam kelimesinin ("ſumma", "summa") baş harfi s'nin biraz evrim geçirmiş ∫ işareti ile gösterilir. Bu işaret Gottfried Wilhelm Leibniz tarafından tanımlanmıştır.

${\displaystyle F(x)=\int f(x)+c,}$

c bir sabiti gösterir ve integralin bir sabit farkı ile bulunabileceğine işaret eder.

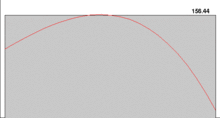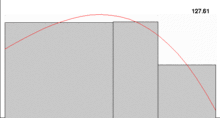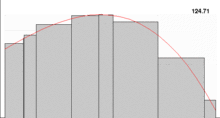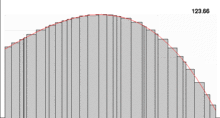
Bir eksen takımında gösterilen f(x) göndermesinin altında kalan a < x < b aralığındaki alan, integral yardımıyla hesaplanabilir. Bu amaçla alan küçük dikdörtgenlere bölünerek, bunların alanı hesap edilip toplanır. Dikdörtgen sayısı arttıkça toplam eğri altındaki alan, alanın değerine yaklaşır ve integralin tam değeri bulunmuş olur. Bu toplama Riemann toplamı denir. İntegralin Riemann anlamındaki tanımı Riemann toplamındaki bölüntü sayısı olan n nin bir limit içerisinde sonsuza götürülmesiyle elde edilir.

${\displaystyle S=\lim _{\Delta x\to 0}\sum _{i=0}^{n-1}f(x_{i})\Delta x_{i}=\int _{a}^{b}f(x)\,dx=F(b)-F(a)}$

Bu şekildeki integral belirli sınırlar arasında hesaplandığı için, belirli İntegral olarak isimlendirilir. Sınırlar göz önüne alınmadan hesaplanan integrale ise belirsiz integral denir. Bazı durumlarda f(x) göndermesinin integrali F(x) bulunamaz. Bu durumda belirli integral sayısal olarak hesaplanır.

Uzunluk, alan ve hacimlerin hesaplanmasında integral hesabın önemli yeri vardır. Birden fazla değişkene bağlı fonksiyonlarda integral kavramı genişletilebilir ve bu durumda katlı integraller ortaya çıkar.

Riemann'dan sonra soyut kümelerin de integrallenebilmesi amacıyla Lebesgue integrali geliştirilmiştir.

Köken

Sir Isaac Newton

Bernhard Riemann

• Dilimize İngilizceden veya Fransızcadan geçmiş integral sözcüğü "bütüne ait olan" anlamına gelir ve İngilizceye Orta Fransızca intégral sözcüğünden; Orta Latince integralis (tüm yapmak, tümlemek) sözcüğünden; Latince integer (tüm, bütün, tam) sözcüğünden gelmiştir. Ayrıca integer sözcüğü tam sayı terimine karşılık olarak İngilizceye geçmiştir^[1].
• Türkçede tümlev sözcüğü, Osmanlıca mütemmem ile tamamî sözcüklerinin ve İngilizcedeki integral sözcüğünün anlamını karşılamak için türetilmiştir^[2]. tümlev sözcüğü, "tümlenmiş şey" anlamına gelir. İsimden fiil yapan /-ev,-av/ yapım ekiyle kullanımda olan tümle[mek] fiilinden; isimden fiil yapan /-le[mek]/ yapım ekiyle muhtemelen Öz Türkçe *tüm (bknz. tümen) kökünden türetilmiştir.
• Osmanlıcada mütemmem sözcüğü kullanılmış (Arapçadaki *tm (tam) kökünden gelir) ancak Arapçada şu anda "olgun, evrimleşmiş, bütünleşmiş" anlamındaki tekâmül sözcüğü kullanılmaktadır(kâmil, mükemmel, küme ile aynı kökten: *kml)^[3].

İntegral alma yöntemleri

Değişken değiştirme

Değişken değiştirme, karmaşık problemleri basitleştirmek için kullanılan değişken değiştirme yöntemidir. Bu yöntemde ham (eski) değişken yerine yeni (daha basit) değişken kullanılır. Problem çözüldükten sonra yeni değişken ile elde edilen sonuç, eski değişkende yerine konur.

Basit örnek

Aşağıdaki 6.dereceden bir polinomu ilkel fonksiyon kullanarak çözmek neredeyse imkansızdır. Bunun için değişken değiştirme yöntemini kullanalım:

${\displaystyle x^{6}-9x^{3}+8=0.\,}$

Bu denklemde x³ = u değişken değişimini uygulanırsa aşağıdaki denklem elde edilir:

${\displaystyle u^{2}-9u+8=0\,}$

Böylece denklem ikinci dereceden denklem biçimine dönüştü. Bu denklemin kökleri;

${\displaystyle u=1\quad {\mbox{ve}}\quad u=8'dir.}$

Bu yeni değişkenin sonuçlarını, ham değişkende yerine koyalım:

${\displaystyle x^{3}=1\quad {\mbox{ve}}\quad x^{3}=8\quad \Rightarrow \qquad x=(1)^{1/3}=1\quad {\mbox{ve}}\quad x=(8)^{1/3}=2.\,}$

Basit fonksiyonların integralleri

Rasyonel fonksiyonlar

${\displaystyle \int dx=x+C}$

${\displaystyle \int x^{n}\,{\rm {d}}x={\frac {x^{n+1}}{n+1}}+C\qquad {\mbox{ eğer }}n\neq -1}$

${\displaystyle \int {dx \over x}=\ln {\left|x\right|}+C}$

${\displaystyle \int {dx \over {a^{2}+x^{2}}}={1 \over a}\arctan {x \over a}+C}$

İrrasyonel fonksiyonlar

${\displaystyle \int {dx \over {\sqrt {a^{2}-x^{2}}}}=\arcsin {x \over a}+C}$

${\displaystyle \int {-dx \over {\sqrt {a^{2}-x^{2}}}}=\arccos {x \over a}+C}$

${\displaystyle \int {dx \over x{\sqrt {x^{2}-a^{2}}}}={1 \over a}\sec {|x| \over a}+C}$

Logaritmik fonksiyonlar

${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C}$

${\displaystyle \int \log _{b}{x}\,dx=x\log _{b}{x}-x\log _{b}{e}+C}$

Üslü fonksiyonlar

${\displaystyle \int e^{x}\,dx=e^{x}+C}$

${\displaystyle \int a^{x}\,dx={\frac {a^{x}}{\ln {a}}}+C}$

${\displaystyle \int a^{ln(x)}\,dx=\int x^{ln(a)}\,dx={\frac {x\,a^{ln(x)}}{\ln {a}+1}}+C={\frac {x\,x^{ln(a)}}{\ln {a}+1}}+C}$

Trigonometrik fonksiyonlar

${\displaystyle \int \sin {x}\,dx=-\cos {x}+C}$

${\displaystyle \int \cos {x}\,dx=\sin {x}+C}$

${\displaystyle \int \tan {x}\,dx=-\ln {\left|\cos {x}\right|}+C}$

${\displaystyle \int \cot {x}\,dx=\ln {\left|\sin {x}\right|}+C}$

${\displaystyle \int \sec {x}\,dx=\ln {\left|\sec {x}+\tan {x}\right|}+C}$

${\displaystyle \int \csc {x}\,dx=\ln {\left|\csc {x}-\cot {x}\right|}+C}$

${\displaystyle \int \sec ^{2}x\,dx=\tan x+C}$

${\displaystyle \int \csc ^{2}x\,dx=-\cot x+C}$

${\displaystyle \int \sec {x}\,\tan {x}\,dx=\sec {x}+C}$

${\displaystyle \int \csc {x}\,\cot {x}\,dx=-\csc {x}+C}$

${\displaystyle \int \sin ^{2}x\,dx={\frac {1}{2}}(x-\sin x\cos x)+C}$

${\displaystyle \int \cos ^{2}x\,dx={\frac {1}{2}}(x+\sin x\cos x)+C}$

${\displaystyle \int \sec ^{3}x\,dx={\frac {1}{2}}\sec x\tan x+{\frac {1}{2}}\ln |\sec x+\tan x|+C}$

${\displaystyle \int \sin ^{n}x\,dx=-{\frac {\sin ^{n-1}{x}\cos {x}}{n}}+{\frac {n-1}{n}}\int \sin ^{n-2}{x}\,dx}$

${\displaystyle \int \cos ^{n}x\,dx={\frac {\cos ^{n-1}{x}\sin {x}}{n}}+{\frac {n-1}{n}}\int \cos ^{n-2}{x}\,dx}$

${\displaystyle \int \arctan {x}\,dx=x\,\arctan {x}-{\frac {1}{2}}\ln {\left|1+x^{2}\right|}+C}$

Hiperbolik fonksiyonlar

${\displaystyle \int \sinh x\,dx=\,coshx+C}$

${\displaystyle \int \cosh x\,dx=\sinh x+C}$

${\displaystyle \int \tanh x\,dx=\ln |\cosh x|+C}$

${\displaystyle \int {\mbox{csch}}\,x\,dx=\ln \left|\tanh {x \over 2}\right|+C}$

${\displaystyle \int {\mbox{sech}}\,x\,dx=\arctan(\sinh x)+C}$

${\displaystyle \int \coth x\,dx=\ln |\sinh x|+C}$

${\displaystyle \int {\mbox{sech}}^{2}x\,dx=\tanh x+C}$

Ters hiperbolik fonksiyonlar

${\displaystyle \int \operatorname {arcsinh} x\,dx=x\operatorname {arcsinh} x-{\sqrt {x^{2}+1}}+C}$

${\displaystyle \int \operatorname {arccosh} x\,dx=x\operatorname {arccosh} x-{\sqrt {x^{2}-1}}+C}$

${\displaystyle \int \operatorname {arctanh} x\,dx=x\operatorname {arctanh} x+{\frac {1}{2}}\log {(1-x^{2})}+C}$

${\displaystyle \int \operatorname {arccsch} \,x\,dx=x\operatorname {arccsch} x+\log {\left[x\left({\sqrt {1+{\frac {1}{x^{2}}}}}+1\right)\right]}+C}$

${\displaystyle \int \operatorname {arcsech} \,x\,dx=x\operatorname {arcsech} x-\arctan {\left({\frac {x}{x-1}}{\sqrt {\frac {1-x}{1+x}}}\right)}+C}$

${\displaystyle \int \operatorname {arccoth} \,x\,dx=x\operatorname {arccoth} x+{\frac {1}{2}}\log {(x^{2}-1)}+C}$

Ayrıca bakınız

• Temel göndermelerin integralleri için İntegral Tablosu
• Belirli integral
• Belirsiz integral
• Karmaşık integral
• İntegral teoremleri

Kaynakça

1. Douglas Harper, Online Etymology Dictionary, sözcük
2. Türk Dil Kurumu, Bilim ve Sanat Terimleri Ana Sözlüğü, sözcük
3. Mustafa Nihat Özön, Osmanlıca - Türkçe Sözlük, İnkılâp ve Aka kitabevleri, 4. basım, Ocak 1965