Varyans analizi

Varyans Analizi (veya ANOVA, İngilizce ANalysis Of VAriance sözcüklerinin kısaltması) istatistik bilim dalında, grup ortalamaları ve (gruplar içi ve gruplar arası varyasyon gibi) bunlara bağlı olan işlemleri analiz etmek için kullanılan bir istatistiksel modeller koleksiyonudur. Varyans Analizi kullanılmaktayken belirlenmiş bir değişkenin gözümlenen varyansı farklı değişim kaynaklarına dayandırılabilen varyans bileşenine ayrılır. En basit şekliyle "Varyans Analizi" birkaç grubun ortalamalarının birbirine eşit mi eşit değil mi olduğunu sınamak için bir çıkartımsal istatistik sınaması olur ve bu sınama iki-grup için yapılan t-test sınamasını çoklu-gruplar için genelleştirir. Eğer, çoklu değişkenli analiz için birbiri arkasından çoklu iki-örneklemli-t-sınaması yapmak istenirse bunun I. tip hata yapma olasığını artırma sonucu doğurduğu aşikardır. Bu nedenle, üç veya daha fazla sayıda (gruplar için veya değişkenler için) ortalamaların ististiksel anlamlığının sınama ile karşılaştırılması için Varyans Analizleri daha faydalı olacağı gerçeği ortaya çıkmaktadır.

Kısacası, ANOVA bir parametrik çıkarımsal metodu olup anakütle ortalamaları arasında farkın olup olmadığını sınamak için kullanılır. Örneğin, 'Opel ile Toyota marka araçların benzin tüketim ortalamaları aynıdır' H₀ hipotezinin sınaması yapılır. Sonuç, "ortalamalar aynıdır" veya "ortalamalar aynı değildir" şeklinde çıkartılır. Bu analizdeki iki değişken arasında lineer bağlantı için (regresyon analizinde yapıldığı gibi) herhangi bir eğim katsayısı bulunmadığı kabul edilir. ANOVA analizi yapılabilmesi için en temel şart, ortalamaları incelenecek olan anakütlelerin varyanslarının aynı olmasıdır.

Bu yöntem ilk defa İngiliz istatistikçi ve genetikçi Ronald Fisher tarafından 1920'lı ve 1930'lu yıllarda geliştirilmiştir. Genel olarak istatistiksel anlamlılık sınamaları içinde F-dağılımını kullanmaları ile karakterize edildikleri için bazen bu analize Fisher'in varyans analizi adı da verilmektedir.

Arka plan ve terminoloji

"Varyans Analizi" deneysel verilerin analiz edilmesi için özellikle pratikte çok defa kullanılan özel bir istatistikel hipotez sınaması şeklidir. İstatistiksel hipotez sınaması bir veriler kullanarak karar vermek yöntemidir. Bir örneklem ve sıfır hipotezden hesaplanmış sınama sonucunun istatistiksel anlamsal olduğunu bildirmek bu sonucun (sıfır hipotezin doğru olduğu kabul edilirse) şans eseri olarak ortaya cıkmasının pek olası olmadığını bildirmek ve kabul etmektir. (Eğer bir olasılık p-değeri bir anlamlılık seviyesi eşik değerinden daha düşük ise) bir istatistiksel anlamlı sonuç sıfır hipotez'in rededilmesini haklı çıkartır.

"Varyans Analizi"'nin uygulandığı tipik bir problemde sıfır hipotez basitçe tüm grupların aynı anakütleden ayrı ayrı basit olasılık örneklemleri ile elde edildiğidir. Bu ise büüun sağaltım işlemlerinin aynı etki (hatta hiçbir etki) vermediğine işaret etmektedir. Böylece sıfır hipotezin reddedilmesi değişik sağaltim işlemlerinin degişme yaratan etkileri olduğunu kabul etmeyi ima etmektedir.

Fena olmayan bir uyma

Hiç uyma olmamasi

Çok güzel uyma olması

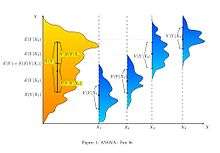
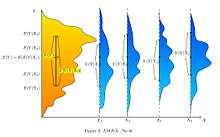
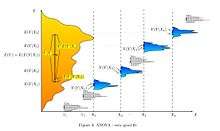
Çıkartımsal istatistik ana kurulma kurallarına göre hipotez sınaması I. Tip Hata yapma haddini (yani hatalı bilimsel iddialara yol açan hatalı poztifleri) bir anlamlılık seviyesi ile sınırlamaktadır. Deneyciler aynı zamanda II. Tip hataları (yani bilimsel bulguları çıkartma fırsatının kaçırılmasına neden olan hatalı negatifleri) sınırlamak istemektedirler. II. Tip Hata haddi çeşitleri nedenlerin fonksiyonudur ve bunlar arasında şunlar bulunur: (a) Örneklem büyükluğü (deneylem maliyetleri ile pozitif korelasyonlu olarak birlikte değişir). (b) Anlamlılık seviyesi (ispat için gereken standartlar çok sıkı ise bir yapılabilecek bir bulgu gözden kaçırma olasılıkları da yüksek olmaktadır). (c) Etki büyüklüğü (etkiler harhangi bir alalade gözlemciye çok aşikar görünmekteyse II. Tip Hata hadleri düşüktür.)

"Varyans Analizi" için kullanılan terminoloji istatistiksel çogunlukla deneysel tasarım için kullanılan terimlerle aynıdır. Deney yapan, bir "etki"yi tespit etmek girişimi ile "faktörler"'i ayarlar ve "yanıtlar"ı ölçer. Sonuçların geçerliligini sağlamak için "faktörler"i deneyleme birimlerine "rassallaştırma" ve "bloklama" karışımı ile ulaştırır. Deneysel "körleştirme" ağırlıkların tarafsız olmasını sağlar. "Yanıt"lar, kısmen etki sonucu olarak kısmen de rassal hata dolayısıyla, bir değişebilirlik gösterir.

"Varyans Analizi" çesitli düşünce tarzlarının bir sentezidir ve çok değişik maksatlarla kullanılmaktadır. Bu nedenle bu analizi çok özlu veya kesinlikle tanımlamak gayet zordur.

"Dengeli veriler için klasik Varyans Analizi üç değişik şeyi aynı anda yapmaktadır:

1. "Veri açıklama analizi": Varyas Analizi toplamalı verilerin ayrışımın organize edilmesidir. Bunun karesel toplamı ayrışımın her bileşenin varyansını (yahut eşit anlamalı olarak bir lineer modelin terimlerini) göstermektedir.

1. "Ortalama karelerin karşılastırılması; F-sınamaları ile... modellerin iç-içine geçmiş ardışıklı olarak sınanmasını sağlama.

1. Varyans Analizi ile çok yakın ilişkili olarak bir lineer modelin katsayı kestirimleri ve standart hataları ile verilere uygulanması." ^[1]

Kısaca ifade ile Varyans Analizi çözumlenen veriler için bir açıklama geliştirme ve doğrulaması için birkaç ceşit analiz yolu olarak kullanılan istatistiksel alettir.

Buna ek olaark

1. Analiz için hesaplamaların "zarif" olduğu ve sonuçlarının varsayımlarının ihlalleri hallerine karşı

nispeten güçlü olduğu bilinmektedir.

1. Varyans Analizi (çoklu örneklem karşılastırmaları ile) sanayi için uygun güçlü analiz sağlamaktadır.
2. Çok çesitli deneylem tasarımının analizi için hemen adapte edilebilmektedir.

Bu nedenle

• Varyans Analizi " psikoloji bilimi araştırmalarında en çok kullanılan (bazılarına göre en kötüye kullanılan) istatistik tekniği olma statüsünde pek uzun zamandır kalmıştır.".^[2]
• Varyans Analizi "mutlaka çıkartımsal istatistik alanında en çok kullanışlı teknik olduğu " iddia edilebilir." ^[3]

Varyans Analizi'nin özellikle karmaşık deneysel tasarılar için öğretilmesi ve öğrenilmesi gayet zordur ve bu arada "sınırlandırılmış rassallaştırma" konusu gayet kötü şöhret yapmıştır.^[4] Bazı hallerde yöntemin tam uygunlukla kullanılabilmesi için, önce görüntülü tanıma yöntemi ile belirlenmesi gerekmete ve sonra da en iyi yetkili klasik testi uygulayarak bir "konsaltasyon" rejimi kullanmak gerekmektedir.^[5]

Deneysel tasarım terimleri

Dengeli tasarım

Her bir hücresinde (yani her ikili sağlatım bileşkenleri için) aynı sayıda gözlem bulunan deneysel tasarım.

Bloklama

Model sınıfları

Varyans Analizi'nde üç değişik sınıf model kullanılmaktadır. Bunlar şöyle özetlenebilir:

Sabit etki modelleri

Verinin normal dağılım gösteren bir anakütleden geldiğini ve ancak farklı ortalamalar dolayısıyla ayrım yapılabileceğini varsaymaktadırlar.

Rastgele etki modelleri

Verinin bir farklar hiyerarşisi ile sınırlanmış olan değişik hiyerarşi içeren anakütlelerden geldiğini varsayar.

Karışık etki modelleri

Içinde hem sabit etkiler hem de rastgele etkiler kapsayan durumları inceler.

Pratik problemlerde varyans analizi deneylemler için kullanılır ve deneylem elemanlarına uygulanan sağlatımların sayısına ve nasıl uygulandıklarına göre birkaç değişik tipe sınıflandırılmaktadırlar:

Tek-yönlü varyans analizi

Bu tür analiz iki veya daha çok sayıda bağımsız grup arasındaki farklılıkların sınanması istenildiği hallerde uygulanır. Tıpık olarak tek yönlü varyans analizi en aşağı üç değişik grup olduğu zaman uygulanmaktadır. İki-grup halinde daha kolay olarak t-sınaması aynı sonuçları vermektedir; çünkü bu halde t-sınaması ve F-sınaması birbirine çok yakından ilişkilidir. Bu yakın ilişki şöyle ifade edilir:

${\displaystyle F=t^{2}}$.

Tekrarlanan ölçülerle tek-yönlü varyans analizi

Bu tür varyans analizinde aynı elamanlara her değişik sağlatım uygulanır, yani elamanlar tekrarlanan ölçülere tabi tutulurlar. Bu yöntem kullanılırken elemanlar kalıntı etkilerine maruz kalabilirler.

Faktōryel varyans analizi

Bu tür varyans analizi eğer deneyci iki veya daha çok sayıda sağlanım (bağımsız) değişkenin etkilerini incelemek isterse kullanılır. En çok kullanılan faktōryel varyans analizi iki bağımsız değişken ve her değişken için iki değişik değer veya seviye olduğu 2x2 (ikiye iki) tasarımdır. Faktōryel varyans analizi çoklu seviyeli, 3x3 (üçe üç) veya daha yüksek sıralı 2x2x2 (ikiye ikiye iki) vb. deneylem tasarımlarında da kullanılabilirler. Ancak bu daha yüksek sayıda faktörler için analizler çok nadir olarak yapılmaktadır. Buna neden hesapların çok karmaşık ve uzun olması ve ortaya çıkartılan sonuçların açıklanmalarının çok zor olduğudur.

Karışık tasarım varyans analizi

Eğer iki veya daha çok sayıda bağımsız gruplar elemanlarına tekrar edilen ölçüler uygulayıp sınanmak istenirse, bir faktöryel karışık tasarım varyans analizi gerçekleştirilebilinir. Bunda bir faktör bağımsız olur ve diğer faktör tekrar edilebilir ölçülere bağlıdır. Bu, karışık etkiler modeline bir örnektir.

Çoklu değişirli varyans analizi

Birden çok bağımlı değişken bulunduğu zaman bu tür varyans analizi kullanılır.

Modeller

Sabit etkiler modelleri

Varyans analizi içinde sabit etkiler modeli, bir deneylem içinde deneycinin deney örneklem elemanlarına yanıt değişkeni değerlerinin birkaç değişik sağlanım uyguladığı zaman değişip değişmediğini incelemek istediği hallere tatbik edilir. Bu modeller deneyciye sağlanımın tüm anakütle içinde ortaya çıkarabileceği yanıt değişken değerlerinin açıklığını kestirim yapma imkâni sağlar.

Rastgele etkiler modelleri

Rastgele etkiler modelleri, sağlanımlar sabit olmadıkları hallerde kullanılırlar. Bu (faktör seviyeleri adı ile de bilinen) değişik sağlanımlar daha büyük bir anakütleden örneklem ile bulunmaları halidir. Sağlanımları kendileri rassal değişken olmaları nedeniyle, sabit etkiler modelinden daha değişik bazı varsayımların ve sağlanımların karşılaştırılmaları gerekmektedir.

Rastgele etkiler modelerinin veya karışık etki modellerinin çoğunda iyi belirenmiş örneklemi alınmış faktörleri ilgilendiren çıkarımsal istatistik analizlerle ilgili değildir. Bunu bir orneğinle açıklamak şöyle yapilabilir: Aynı mali üretmek için çok değişik makinaların kullanıldığı bir sanayi birimi ele alınsın. Bu işletmeyi inceleyen istatisikçi üç değişik makinenin birbirleri ile karşılaştırılması ile ilgilenmesi uygulanabilen pratik bir problem degildir. Buna karşılık tüm makinalar hakkında, tüm ortalama üretkenlik ve değişik makinelerde üretkenliğin yayılımı hakkında çıkarımsal istatistik analizi sınamalar arastirmaciyi ilgilendiren bir sorun olabilir.

Varsayımlar

• İstatistiksel bağımsızlık: Bu varsayım deneylem tasarımı için gerekmekte ve sağlatım uygulanan elamanların bağımsız oldukları varsayılmaktadır.
• Normallik: Her bir grup içindeki elamanların normal dağılım gösteren anakütlelerden geldikleri varsayılır. Verilerinin normallik özelliği olup olmadığı ya normallik sınamaları olan Kolmogorov-Şmirnov sınaması veya Shapiro-Wilk sınaması kullanılarak incelenebilir. Normallik varsayımını incelemek için parametrik olmayan istatistik sınaması olan Kruskal-Wallis sınaması da kullanılabilir.
• Eşit varyanslar veya heteroskedastiklik: Homoskadastiklik halinde her bir grup elemanlarının geldikleri anakütlelerde varyansların aynı olduğu varsayılır. Verilerin eşit varyanslar varsayımına uyup uymadıklarını sınamak için tipik olarak Levene'in sınamasi kullanılır. Ama "Levene'in sinamasi" icin grup gözlem sayılarınin eşit olmasi gerekir. Daha degisik hallerde eger gruplarda sapan değer yoksa "Bartlet Sinamasi" veya gruplarda gözlem sayıları eşitse "Cochran Varyans Eşitliği Sinamasi" kullanılır.

Bazı istatistikçiler verilerin normallikten ayrılması halinde varyans analizinin esası olan F-sınaması'nın güvenilmez olacağını bildirmektedir ^[6]. Diğer istatistikçiler ise F-sınamasının "güçlü olduğunu", yani normal olmamakdan fazla etkilenmediğini savunmaktadırlar.^[7]

Bu ortak varsayımlar yanında sabit etki modelleri için hataların bağımsız ve aynı şekilde normal dağılım gösterdikleri de, yani

${\displaystyle \varepsilon \thicksim N(0,\sigma ^{2}).\,}$

olduğu varsayılmaktadır. Varyans analizi için kullanılan rastgele etki modelleri ve karışık etki modelleri için hataların ortalama ve varyansi için daha karmaşık varsayımlar gerekmektedir çünkü faktörler kendilerine özel dağılımlardan ortaya çıkartılabilirler.

Varyans analizinin inceleme yaklaşımı

Varyans analizinde temel yöntem, toplam kareler toplamını modelde kullanılan etkilere uygun olan parçalara bölmektir. Bu yönteme aşağıda verilen örnek tek bir sağlatımın değişik seviyelere uygulanması halidir.

Kareler toplamının parçalara bölünmesi

Örnek olarak tek bir sağlatımın değişik seviyeler uygulanması sonucu ortaya çıkan toplam kareler toplamı şu parçalara bölünür:

${\displaystyle SS_{\hbox{Toplam}}=SS_{\hbox{Hata}}+SS_{\hbox{Sağlanım}}\,\!}$

Serbestlik dereceleri de aynı şekilde parçalara bölünmektedir ve her ilgili parçanın bir ki-kare dağılımı gösterdiği belirlenmektedir.

F-sınaması

Toplam sapmanın parçalarının karşılaştırılması için F-sınaması uygulanır. Tek yönlü veya tek faktörlü varyans analizi için istatistik anlamlılığın sınanması, F-sınama istatistiği olan şu

${\displaystyle F={\dfrac {\mbox{grup ortalamaları varyansı}}{\mbox{grup-içindekiler varyansı ortalaması}}}}$

${\displaystyle F^{*}={\frac {\mbox{MSTR}}{\mbox{MSE}}}}$

burada:

${\displaystyle {\mbox{MSTR}}={\frac {\mbox{SSTR}}{I-1}}}$, İ = sağlatımlar sayısı

ve

${\displaystyle {\mbox{MSE}}={\frac {\mbox{SSE}}{n_{T}-I}}}$, n_T = toplam gözlem eleman sayısı

ifade ile I-1 ve n_T serbestlik derecelerinde F-dağılımı ifadesini karşılaştırmak suretiyle gerçekleştirilir.

F-dağılımı kullanmak doğal bir uygulamadır, çünkü sınama istatistiği her biri ki-kare dağılımı gösteren iki kareler toplamları ortalamasının bir diğerine bölümüne eşittir.

Ayrıca bakınız

• Covaryanslar analizi
• Duncan'ın yeni çoklu açıklık sınaması
• açıklanan varyans ve açıklanmayan varyans
• Çok değişirli varyans analizi
• F-testi
• Ölçüm belirsizliği
• Sapmaların karesi
• Çoklu karşılaştırmalar
• t-sınaması
• Kruskal-Wallis sınaması
• Friedman sınaması

Kaynakça

1. Gelman (2005, s 2)
2. Howell (2002, s.320)
3. Montgomery (2001, s.63)
4. Gelman (2005, s.1)
5. Gelman (2005, s.5)
6. Lindman,H.R. (1974), Analysis of variance ın complex experimental designs. San Francisco: W. H. Freeman & Co.
7. Ferguson,G.A. ve Takane,Y. (2005), Statistical Analysis in Psychology and Education 6.Ed.. Montréal, Quebec: McGraw-Hill Ryerson Ltd.

Dış kaynaklar

• Oxford Üniversitesi psikoloji bölümü öğrencileri için varyans analizine giriş dersi (İngilizce) (Erişim:17.3.2010)
• Rasgeleleştirilmiş blok, ayırılmış parseller, tekrarlanan ölçüler ve Latin kareler deneylem tasarımlarını kapsayan üç sağlatıma kadar tüm varyans analizi ve çoklu değişirli varyans analizi modelleri için örnekler (İngilizce) (Erişim:17.3.2010)
• NİST/SEMATECH e-Handbook of Statistical Methods, section 7.4.3: "Are the means equal?" İstatistik Yöntemler Kılavuzu. (İngilizce) (Erişim:17.3.2010)
• TDS1 Belirsizlik Hesaplayıcısı (İngilizce) (Erişim:17.3.2010)