Asal çarpanlara ayırma

Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.

Sayılar çok büyük olduğunda, kuantum olmayan hızlı bir algoritma bilinmemektedir. 2009 yılında sonuçlanan bir çalışmada bir grup araştırmacı 232 basamaklı bir sayıyı (RSA-768), yüzlerce makinayı iki yıl boyunca çalıştırarak çarpanlarına ayırmışlardır.^[1] Bu problemin varsayılan zorluğu, kriptografi alanında sıkça kullanılan RSA gibi algoritmaların tasarımında çok önemli bir yere sahiptir. Bu problem, eliptik eğriler, cebirsel sayı kuramı ve kuantum hesaplama gibi matematik ve bilgisayar biliminin birçok alanında önem arz etmektedir.

Belli uzunluktaki her sayının çarpanlara ayrılma zorluğu aynı değildir. Çarpanlara ayrılması en zor sayılar (halihazırda bilinen teknikler ışığında) yarıasallar, yani iki asal sayının çarpımı şeklinde yazılabilen sayılardır. Bu sayılardan ikisi de büyük, mesela 2000 bit uzunluğunda ve rastgele, birbirleriyle yakın uzunlukta (fakat çok yakın değil, çünkü böyle sayılar için Fermat'ın çarpanlara ayırma metodu kullanılabilir) olacak şekilde seçildiği takdirde, en hızlı çarpanlara ayırma algoritmaları en hızlı bilgisayarlarda dahi çalışsa pratikte kullanılabilecek bir hızda çözüme ulaşamamaktadır. Çarpanlara ayrılacak sayının asal çarpanlarının bit uzunlukları arttıkça algoritmanın çalışma süresi şiddetli biçimde artmaktadır.

RSA gibi çok sayıda kriptografik protokol bu problemin veya bir benzerinin zorluğuna dayanmaktadır. Bir başka deyişle eğer bir sayıyı hızlı bir şekilde çarpanlara ayırma algoritması bulunsaydı, RSA tabanlı açık anahtar kriptografisi güvenliğini yitirirdi.

Asallara ayırma

864 sayısının asal çarpanlarına ayrılması. Asal çarpanları yazmanın kısa bir yolu: ${\displaystyle 2^{5}\times 3^{3}}$

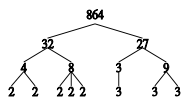
Aritmetiğin temel teoremi gereğince, her pozitif tamsayı asal çarpanlarına tek bir biçimde ayrılır (1 için özel bir duruma gerek yoktur, boş çarpım tanımının olması yeterlidir). Fakat,aritmetiğin temel teoremi bu çarpanların nasıl bulunacağı konusunda bir şey söylemez; sadece var olduklarını söyler.

Genel bir çarpanlara ayırma algoritması verildiğinde, bu algoritmayı tekrar tekrar uygulamak suretiyle herhangi bir tamsayı asal çarpanlarına kadar ayrılabilir. Fakat özel bir amaca yönelik bir çarpanlara ayırma algoritması için bu söz konusu değildir çünkü bu özel algoritma daha ayrıştırmanın sonraki adımlarındaki daha küçük çarpanlara ayırma problemlerinde işe yaramayabilir veya çok yavaş çalışabilir. Mesela deneme bölmesi N = 2 × (2⁵²¹ − 1) × (2⁶⁰⁷ − 1) için 10N sayısını hızlı bir biçimde 2 × 5 × N olarak çarpanlara ayırır ama N sayısını hızlı bir biçimde çarpanlarına ayıramaz.

En son gelişmeler

Çarpanlarına ayrılması en zor tamsayılar birbirine yakın uzunluktaki iki büyük asal sayının çarpımı şeklinde olanlar, bir başka deyişle yarıasallardır. Tam da bu yüzden kriptografide bu sayılar kullanılmaktadır. Halihazırda çarpanlarına ayrılmış en büyük yarıasal 232 basamaklı, 768-bitlik bir sayıdır. (12 Aralık 2009) ^[1] Çeşitli araştırma enstitülerinin ortak çalışmasıyla yapılan bu işlem, iki yıl sürmüş ve tek çekirdekli bir 2.2 GHz AMD Opteron bilgisayarın 2000 yıl çalışmasına denk bir işlem gücüne mal olmuştur. Diğer tüm çarpanlara ayırma rekorları gibi bu rekor da genel sayı cismi eleme (GNFS) algoritmasının son derece optimize bir şekilde yüzlerce makine üzerinde çalıştırılmasıyla tamamlanabilmiştir.

Zorluk ve karmaşıklık

Eğer b bitlik büyük bir sayı yaklaşık aynı uzunlukta iki asal sayının çarpımı ise, yayınlanmış hiçbir algoritma bu sayıyı polinomsal zamanda (yani belli bir k değeri için Yani O(b^k) zamanda) çarpanlarına ayıramamaktadır. Tüm pozitif ε değerleri için O((1+ε)^b)'den daha hızlı yani üstel-altı zaman algoritmalarsa yayınlamış bulunmaktadır. GNFS algoritmasıyla "b"-bitlik bir yarıasalın çarpanlarına ayrılması için yayınlanmış olan en iyi asimptotik çalışma zamanı,

${\displaystyle O\left(\exp \left(\left({\begin{matrix}{\frac {64}{9}}\end{matrix}}b\right)^{1 \over 3}(\log b)^{2 \over 3}\right)\right)}$tür.

Sıradan bir bilgisayar için, GNFS 100 basamaktan daha büyük sayılarda çalışmak üzere yayınlanmış en iyi algoritmadır. Fakat bir kuantum bilgisayarı için, Peter Shor 1994 yılında polinomsal zamanda çözüme ulaşan bir algoritma keşfetmiştir. Eğer gelecekte büyük bir kuantum bilgisayarı inşa edilebilirse bu keşif kriptografi açısından önemli sonuçlar doğuracaktır. Shor algoritması "b"-bitlik bir girdi için sadece O(b³) zaman ve O(b) yer gerektirmektedir. 2001 yılında, 7-kübitlik bir kuantum bilgisayar ilk kez Shor'un algoritmasını çalıştırmış ve 15'i çarpanlarına ayırmıştır.^[2]

Çarpanlara ayırma probleminin hangi karmaşıklık sınıfına dahil olduğu incelenirken problemin değişik versiyonlarını ayırt etmek gerekir.

• Fonksiyon problemi versiyonu: Bir N tamsayısı verildiğinde 1 < d < N olacak şekilde N'yi bölen bir d sayısı bulunuz (veya N'nin asal olduğu sonucuna varınız). Bu problem FNP'de olup FP'de olup olmadığıysa bilinmemektedir. Pratikte uygulamalarda çözülen versiyon, bu versiyondur.
• Karar problemi versiyonu: 1 ≤ M ≤ N olacak şekilde M ve N tamsayıları verildiğinde, 1 < d < M olacak şekilde öyle bir d sayısı var mıdır ki N'yi bölüyor olsun? Bu versiyon kullanışlıdır çünkü çokça çalışılmış tüm karmaşıklık sınıfları fonksiyon değil karar problemleri üzerinden tanımlanmıştır. Bu, problemin optimizasyon problemleri için sıkça kullanılanlara denk gelen doğal bir karar versiyonudur, çünkü bu versiyon ikisel arama ile birleştirilerek fonksiyon versiyonu da logaritmik sayıda sorgu ile çözülebilir. Çarpanlara ayırma probleminin karar versiyonunun tam olarak hangi karmaşıklık sınıfında yer aldığı bilinmemektedir. Ne var ki hem NP hem de co-NP'de olduğu bilinmektedir. Çünkü asal çarpanlar verildiğinde hem EVET hem de HAYIR cevapları teyit edilebilir. (Çarpanların asallığı AKS asallık testi ile, çarpımlarının N olduğunu da basitçe çarparak kontrol edilebilir.) Aritmetiğin temel teoremince sadece bir çözümün kabul edilebileceği kesindir (sıralı olmaları koşuluyla). Bu da gösterir ki problem hem UP hem de co-UP sınıflarındadır.^[3] Problemin BQP'de olduğu Shor algoritması dolayısıyla bilinmektedir. P, NP-complete, ve co-NP-complete karmaşıklık sınıflarının üçünde de olmadığı sanılmaktadır. Dolayısıyla NP-intermediate karmaşıklık sınıfında olmaya adaydır. NP-Complete veya co-NP-Complete olduğu gösterildiği takdirde, NP = co-NP olması gerekecektir. Oysa bu son derece beklenmedik bir netice olacağı için çarpanlara ayırma probleminin bu iki sınıfta da olmadığı düşünülmektedir. Çok sayıda insan klasik polinomsal-zaman algoritmalar bulmayı deneyip başaramadıklarından yaygın kanı P sınıfının dışında olduğu yönündedir.

Bunlara karşın ""N" bileşik sayı mıdır?" (veya buna denk olarak ""N" asal sayı mıdır?") karar problemleri "N"'nin çarpanlarını bulmaya nazaran çok daha kolay görünmektedir. Bu karar problemlerinden ilki AKS asallık testi ile N'nin basamak uzunluğu cinsinden polinomsal zamanda çözülebilmektedir. Bununla beraber, çok küçük bir hata payına razı olmak koşuluyla çok hızlı sonuç verebilen çeşitli olasılıksal algoritmalar bulunmaktadır. Asallık testinin kolay oluşu, başlangıcında büyük asal sayılar bulma gerekliliğinden dolayı RSA algoritması için büyük önem arz etmektedir.

Çarpanlara ayırma

Amaca özel

Amaca özel bir çarpanlara ayırma algoritmasının çalışma zamanı, çarpanlara ayrılmaya çalışan sayının veya bilinmeyen çarpanlarından birinin özelliklerine bağlıdır: büyüklük, özel form, vs. Tam olarak çalışma süresinin ne olduğuysa algoritmadan algoritmaya değişir.

Amaca özel algoritmaların önemli bir alt sınıfı "1. Kategori" olarak adlandırılan algoritmalardır ki bunların çalışma süreleri en küçük asal çarpanın büyüklüğüne bağlıdır. Formu bilinmeyen bir tamsayı verildiğinde küçük çarpanları ayıklamak için genellikle bu algoritmalar genel algoritmalardan önce çalıştırılır.^[4]

• Deneme bölmesi
• Tekerlek çarpanlara ayırma yöntemi
• Pollard'ın rho algoritması
• Cebirsel-grup çarpanlara ayırma algoritmaları: Pollard'ın p - 1 algoritması, Williams'ın p + 1 algoritması ve Lenstra eliptik eğri çarpanlara ayırma yöntemi
• Fermat'ın çarpanlara ayırma metodu
• Euler'in çarpanlara ayırma metodu
• Özel sayı cismi eleme yöntemi

Genel amaçlı

Aynı zamanda 2. kategori veya kaşifi Maurice Kraitchik'e atfen Kraitchik ailesi algoritmalar ^[4] olarak da bilinen genel çarpanlara ayırma algoritmalarının çalışma süreleri sadece çarpanlarına ayrılacak olan sayının büyüklüğüne bağlıdır. RSA sayılarını çarpanlarına ayırmak için bu algoritmalar kullanılır. Genel çarpanlara ayırma algoritmalarının çoğu kareler çakışması metoduna dayalıdır.

• Dixon algoritması
• Tekrarlı bölme çarpanlara ayırma metodu (CFRAC)
• İkinci derece elek metodu
• Genel sayı cismi eleme metodu
• Shank'in kare formları çarpanlara ayırma metodu (SQUFOF)

Diğer kayda değer algoritmalar

• Kuantum bilgisayarları için Shor algoritması

Sezgisel çalışma süresi

Sayılar teorisinde beklenen çalışma süresi sezgisel olarak, O ve L notasyonu ile ifade edilecek olursa,

${\displaystyle L_{n}\left[1/2,1+o(1)\right]=e^{(1+o(1))(\log n)^{\frac {1}{2}}(\log \log n)^{\frac {1}{2}}}}$

olan birçok çarpanlara ayırma algoritması vardır. Bu algoritmalara bazı örnekler eliptik eğri metodu ve ikinci dereceden elek metodudur. Bu şekilde bir diğer algoritma da Schnorr tarafından önerilen sınıf grup ilişkileri metodudur.^[5] Bu durum Seysen^[6] ve Lenstra^[7] tarafından genelleştirilmiş Riemann hipotezi (GRH) ışığında ispatlanmıştır.

Kesin çalışma süresi

Schnorr-Seysen-Lenstra olasılıksal algoritmasının beklenen çalışma süresinin ${\displaystyle L_{n}\left[1/2,1+o(1)\right]}$ olduğu, Lenstra ve Pomerance^[8] tarafından GRH varsayımı yerine çarpanlar kullanılmak suretiyle kesin bir şekilde ispatlanmıştır. Algoritma, G_Δ ile gösterilen diskriminant Δ'nın pozitif ikili ikinci dereceden fom sınıf grubunu kullanır. G_Δ (a, b, c) gibi aralarında asal tamsayı üçlülerinin kümesidir.

Schnorr-Seysen-Lenstra algoritması

Algoritmanın girdisi, belirli sabit bir değerden büyük, pozitif ve tek bir "n" tamsayısıdır. Bu çarpanlara ayırma algoritmasında, diskriminant Δ, "d" bir pozitif çarpan olmak kaydıyla, Δ= -dn şeklinde "n"'nin bir tam katı olarak seçilir. Algoritma, G_Δ'da bir "d" değeri için yeterli düzgün formlarının olduğunu umar. Lenstra ve Pomerance söz konusu "d"'nin seçiminin belirli küçük bir kümeyle sınırlanarak düzgünlüğün garanti edilebileceğini göstermişlerdir.

P_Δ ile Kronecker sembolü ${\displaystyle \left({\tfrac {\Delta }{q}}\right)=1}$ olan tüm q asal sayılarının kümesini gösterelim. "q" P_Δ'da olmak üzere G_Δ'nın bir üreteç ve asal form f_q kümelerini oluşturmak kaydıyla, üreteçler ve f_q arasında bir bağıntı dizisi üretilir. "q"'nun büyüklüğü bir ${\displaystyle c_{0}}$ değeri için ${\displaystyle c_{0}(\log |\Delta |)^{2}}$ ile sınırlandırılabilir. Kullanılacak olan bağıntı, G_Δ'nın tarafsız elemanına eşit olan üsler çarpımı arasındaki bir bağıntıdır. Bu bağıntılar,, aslında G_Δ'nın kertesi 2'yi bölen bir elemanı olan, G_Δ'nın çokanlamlı bir formunu inşa etmek için kullanılacaktır. Δ'nın ilişkin çarpanlara ayrımını hesaplayarak ve bir EBOB alarak, bu çokanlamlı form "n"'nin tam bir asal çarpanlara ayrımlanmasını verir. Bu algoritmanın ana basamakları şunlardır:

Çarpanlarına ayrılacak sayı "n" olsun.

1. d bir çarpan ve Δ bir ikinci dereceden formun negatif diskriminantı olmak koşuluyla, Δ, -dn şeklinde negatif bir tamsayı olsun.
2. Bir ${\displaystyle t\in {\mathbb {N} }}$ için, ilk t asal sayıyı ${\displaystyle p_{1}=2,p_{2}=3,p_{3}=5,\dots ,p_{t}}$ alalım.
3. ${\displaystyle \left({\tfrac {\Delta }{q}}\right)=1}$ olmak üzere, ${\displaystyle f_{q}}$, G_Δ'nın rassal bir asal formu olsun.
4. G_Δ'nın bir X üretici kümesini bul.
5. "X" kümesi ve {f_q : q ∈ P_Δ} arasında şunu sağlayan bir bağıntı dizisi topla: ${\displaystyle \left(\prod _{x\in X_{}}x^{r(x)}\right).\left(\prod _{q\in P_{\Delta }}f_{q}^{t(q)}\right)=1}$
6. Δ = -4a.c or a(a - 4c) or (b - 2a).(b + 2a) olmak kaydıyla Δ'nın en büyük tek böleninin aralarında asal çarpanlarına ayrımını elde etmek için, derecesi 2'yi bölen bir f ∈ G_Δ elamanı olan bir "(a, b, c)" çokanlamlı formu oluştur.
7. Eğer çokanlamlı form "n"'nin bir çarpanlara ayrımını verirse dur, aksi takdirde "n"'nin bir çarpanlara ayrımı bulunana dek başka bir çokanlamlı form bul. Kullanışsız çokanlamlı formların üretimini en baştan engellemek için G(Δ)'nın S₂(Δ) 2-Sylow grubunu inşa et.

Herhangi bir pozitif tamsayıyı çarpanlarına ayıran bir algoritma elde edebilmek için bu algoritmaya deneme bölmesi, Jacobi toplamı testi gibi birkaç basamak daha eklemek gerekmektedir.

Beklenen çalışma süresi

Verildiği şekliyle algoritma rassal seçimler yapması dolayısıyla olasılıksal bir algoritmadır. Beklenen çalışma süresi en çok ${\displaystyle L_{n}\left[1/2,1+o(1)\right]}$'dir.^[8]

Ayrıca bakınız

• Bir pozitif tam sayının kanonik gösterimi

Kaynakça

1. Kleinjung, et al (2010-02-18). Factorization of a 768-bit RSA modulus. IACR. http://eprint.iacr.org/2010/006.pdf. Erişim tarihi: 2010-08-09. 
2. LIEVEN M. K. VANDERSYPEN, et al (2007-12-27). NMR quantum computing: Realizing Shor's algorithm. Nature. http://www.nature.com/nature/links/011220/011220-2.html. Erişim tarihi: 2010-08-09. 
3. Lance Fortnow (2002-09-13). "Computational Complexity Blog: Complexity Class of the Week: Factoring". 19 Kasım 2008 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20081119034645/http://weblog.fortnow.com/2002/09/complexity-class-of-week-factoring.html. 
4. David Bressoud ve Stan Wagon. A Course in Computational Number Theory. Key College Publishing/Springer. s. 168-69. ISBN 978-1-930190-10-8. 
5. Schnorr, Claus P. (1982). "Refined analysis and improvements on some factoring algorithms". Journal of Algorithms 3 (2): 101–127. DOI:10.1016/0196-6774(82)90012-8. 
6. Seysen, Martin (1987). "A probabilistic factorization algorithm with quadratic forms of negative discriminant". Mathematics of Computation 48 (178): 757–780. DOI:10.1090/S0025-5718-1987-0878705-X. 
7. Lenstra, Arjen K (1988). "Fast and rigorous factorization under the generalized Riemann hypothesis". Indagationes Mathematicae 50: 443–454. 
8. H.W. Lenstra, and C. Pomerance; Pomerance, Carl (July 1992). "A Rigorous Time Bound for Factoring Integers" (PDF). Journal of the American Mathematical Society 5 (3): 483–516. DOI:10.1090/S0894-0347-1992-1137100-0. http://www.ams.org/mcom/2006-75-256/S0025-5718-06-01870-9/S0025-5718-06-01870-9.pdf. 

Ek okumalar

• Richard Crandall ve Carl Pomerance (2001). Prime Numbers: A Computational Perspective. Springer. ISBN 0-387-94777-9.  Chapter 5: Exponential Factoring Algorithms, pp. 191–226. Chapter 6: Subexponential Factoring Algorithms, pp. 227–284. Section 7.4: Elliptic curve method, pp. 301–313.
• Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Section 4.5.4: Factoring into Primes, pp. 379–417.

Dış bağlantılar

• Paolo Ardoino, üç algoritma ve C kaynak kodları.
• asal çarpanlara ayırma: Paul Herman & Ami Fischman, Pollard Rho & Shor da dahil birçok asal çarpanlara ayırma algrotiması için C++ kaynak kodları.

Şablon:Sayılar teorisi algoritmaları