Boyut
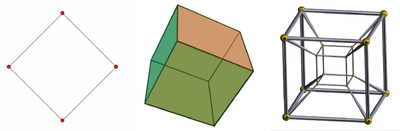
Fizik ve matematikte bir uzayın ya da nesnenin boyutu, gayriresmi olarak bu uzay ve nesne üzerindeki herhangi bir noktayı belirlemek için gereken minimum koordinat sayısı olarak tanımlanır.[1][2] Bir doğru üzerindeki bir noktayı tanımlamak için bir koordinat gerektiğinden doğrunun bir boyutu vardır (örneğin sayı doğrusu üzerindeki 5 noktası). Düzlem, kare ya da daire yüzeyinin iki boyutu vardır, çünkü bu yüzeyler üzerindeki herhangi bir noktayı tanımlamak için iki koordinata ihtiyaç vardır (örneğin kare üzerindeki bir noktayı tanımlamak için hem enleme, hem de boylama ihtiyaç vardır). Yine aynı şekilde küre, silindir ya da küpün içindeki bir noktayı tanımlamak için üç koordinat gerektiğinden bu boşluk üç boyutludur. İzafiyet Teorisi'nde ise zaman, dördüncü ve uzaysal olmayan boyut olarak eklenir.
| Boyutlar | Örnek |
|---|---|
| 0 | Nokta |
| 1 | Doğru |
| 2 | Alan |
| 3 | Hacim |
| 4 | Uzayzaman |
İlave boyutlar
Fizikte üç uzay boyutu ve bir de zaman boyutu kabul gören normdur. Fakat temel kuvvetleri birleştirmeye çalışan teoriler, bu amaçla daha fazla boyut eklemektedirler. Süper sicim teorisi, M teorisi ve Bozonsal sicim teorisi, fiziksel uzayın sırasıyla 10, 11 ve 26 boyutlu olduğunu iddia ederler. Bu ilâve boyutların uzaysal olduğu söylenir. Fakat biz ancak üç uzaysal boyutu algılarız ve bugüne kadar ne deneysel, ne de gözlemsel deliller, ilave boyutların varlığını tasdik etmez. Muhtemel bir açıklama, uzayın atomaltı ölçekte (muhtemelen quark/sicim ölçek seviyesi veya daha altta) ilave boyutların içine "sarılmış gibi" davrandığıdır.
Aralık 2012'de Büyük Hadron Çarpıştırıcısı sonuçlarının analizi, büyük ilave boyutlu teorileri ciddî şekilde sınırlamıştır.[3]
Uzaya ilave boyutlar eklemiş başka fizîki teorilerse şunlardır:
- Kaluza–Klein teorisi, kütle çekimi dışındaki kuvvetleri açıklamak için ilave boyutlar getirir (aslen sadece elektromanyetizma).
- Büyük ilave boyutlar ve Randall–Sundrum Modeli, kütle çekimin zaafını açıklamaya çalışır. Bu özellik brane kozmolojisinde kullanılır.
- Evrensel ilave boyutlar
Ek okumalar
- Edwin A. Abbott, (1884) Flatland: A Romance of Many Dimensions, Public Domain. Online version with ASCII approximation of illustrations at Project Gutenberg.
- Thomas Banchoff, (1996) Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, Freeman.
- Clifford A. Pickover, (1999) Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press.
- Rudy Rucker, (1984) The Fourth Dimension, Houghton-Mifflin.
- Michio Kaku, (1994) Hyperspace, a Scientific Odyssey Through the 10th Dimension, Oxford University Press.
Kaynakça
- ↑ "What is a dimension?". cornell.edu. 4 Haziran 2003. 24 Ocak 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150124042428/http://curious.astro.cornell.edu:80/question.php?number=4. Erişim tarihi: 24 Ocak 2012.
- ↑ "MathWorld: Dimension". mathworld.wolfram.com. 5 Eylül 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150905163417/http://mathworld.wolfram.com/Dimension.html. Erişim tarihi: 24 Ocak 2012.
- ↑ CMS Collaoration, "Search for Microscopic Black Hole Signatures at the Large Hadron Collider," http://arxiv.org/abs/1012.3375