Kapalı zamansı eğri

Kapalı zamansı eğri (KZE) matematiksel fizikte, “kapalı” uzayzamanda, başlangıç noktasına geri dönen bir parçacığın Lorentz manifoldundaki zaman çizgisidir (4 boyutlu uzayda hareket eden parçaların kendine özgü yolu). Bu olasılık ilk defa, genel rölativitenin eşitsizliklerine uygun bir çözüm keşfetmiş olan Kurt Gödel tarafından 1949 yılında ortaya çıkartılmış, KZElerin aynı zamanda Gödel ölçüsü olarak bilinmesini sağlamıştır ve o zamandan beri de Tipler silindiri ve geçilebilir solucandelikleri gibi KZEleri içeren başka genel rölativite çözümleri bulunmuştur. Eğer KZEler varsa, varlıkları geriye doğru zaman yolculuğunu en azından teorik olarak mümkün olduğuna kanıt olarak sunulabilir, bu da büyükbaba paradoksu endişesini ortaya çıkartabilir, ancak Novikov öztutarlılık prensipleri bu tarz paradokslardan kaçınılabileceğini belirtmektedir. Bazı fizikçiler, belirli genel rölativite çözümlerinde yer alan KZElerin, ileride ortaya atılacak ve genel rölativitenin yerine geçecek olan kuantum kütleçekimi teorisiyle denklemden atılabileceğini savunmaktadır, Stephen Hawking bu fikri kronoloji korunumu varsayımı olarak adlandırmıştır. Diğerleri ise, belirli bir uzayzamandaki tüm kapalı zamansı eğrilerin aynı olay ufkundan geçmesi durumunda, ki bu da kronojik sansür olarak isimlendirilebilecek bir özelliktir; bu uzayzaman tüm olay ufuklarından temizlense dahi, yine de düzgün nedensellikte davranacağını ve bir gözlemcinin nedensellik ihlalini tespit edemeyeceğini savunmaktadırlar.[1]

Işık konileri

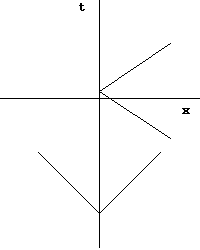
Aşağıdaki ışık konisi yassı uzalardaki ışık konilerinin özelliklerini taşımaktadır –ışık konisinde yer alan tüm koordinatların sonraki bir zamanı vardır. Yukarıdaki koni yalnızca diğer uzamsal konumları göstermekle kalmayıp, bununla beraber x=0 durumunu gelecek zamanlar için dahil etmemekte ve önceki zamanlar için dahil etmektedir

Genel rölativitede bir sistemin evriminden, ya da daha spesifik olmak gerekirse Minkowski uzayından bahsederken, fizikçiler çoğunlukla “ışık konisi”ne başvururlar. Işık konisi; mevcut durumu verilen bir cismin gelecekte geçireceği tüm muhtemel evrimleri temsil eder, ya da mevcut konumu verilen cismin tüm olası konumları. Cismin olası gelecek konumları, hareket edebileceği hızla sınırlıdır ve bu da en fazla ışık hızı olabilir. Örneğin, t0 anında p konumunda bulunan bir cisim t1 zamanına kadar yalnızca c(t1 − t0) sınırında bulunan konumlarda yer alabilir.

Bu genelde konumlar yatay, geçen zaman da dikey eksende uzanacak şekilde; zaman için t ve uzay için ct birimleri kullanılarak grafikte gösterilir. Buradaki temsilde ışık t zamanda ct birim yol alırken ışık konisi, cismi merkez alan 45 dereceli açılarla gösterilmiştir. Böyle bir diyagramda, cismin gelecekteki tüm olası konumları koni üzerinde yer almaktadır. Buna ek olarak, her uzay konumunun bir gelecek zamanı vardır, bunun anlamı da herhangi bir cismin uzaydaki herhangi bir konumda süresiz olarak kalabileceğidir.

Bu diyagram üzerindeki her bir noktaya durum denir. Ayrık durumlara, eğer zaman ekseni boyunca ayrılmışlar ise zamansı ve eğer uzay ekseni boyunca ayrılmışlarsa uzaysı denir. Eğer cisim serbest düşüşte olsaydı, t-ekseni boyunca yukarı yönde hareket edecek; eğer ivmelenirse aynı zamanda x ekseninde de hareket edecektir. Cismin izleyebileceklerinin aksine, uzayzamanda izlediği esas yola zaman çizgisi denir. Bir diğer tanım da, ışık konisinin tüm muhtemel zaman çizgilerinin temsili olduğudur.

“Basit” uzayzaman metriklerinde ışık konisi zamana doğru yönelmektedir. Bu da bir cismin aynı anda iki yerde bulunamayacağı olgusuna tekabül etmektedir, alternatif bir tanımsa cismin anlık olarak başka bir konuma gidemeyeceğidir. Bu uzayzamanlarda fiziksel cisimlerin zaman çizgileri, tanımsal olarak zamansıdır. Ancak bu yönelim yalnızca “lokal yassı” uzayzamanlar için geçerlidir. Eğimli uzayzamanlarda ışık konisi, uzayzamanın jeodeziğine doğru yana yatacaktır. Örneğin, bir yıldızın yakınlarında hareket ederken cisim yıldızın yerçekimi tarafından “çekilecek”, cismin zaman çizgisini etkileyecektir, bu yüzden de gelecek pozisyonların yıldızlara yakın şekilde uzanması olasıdır. Bu da denk gelen uzayzaman diyagramına doğru hafif yana yatmış bir ışık konisi olarak temsil edilmektedir. Bu koşullar altında serbest düşüşte olan bir cisim lokal t ekseninde ilerlemeye devam eder ancak dışarıdan bakan bir gözlemciye göre uzayda da ivmelenmekte olduğu görülecektir – örneğin cisim yörüngede değilse bu yaygın bir durumdur.

Uç örneklerde, uygun derecede yüksek eğimli metrike sahip uzayzamanlarda, ışık konisi 45 dereceden daha fazla da yana yatabilir. Bunun anlamı, cismin referans sistemine göre harici bir nihai koordinattan bakan gözlemcinin uzaysı ayrılmış potansiyel “gelecek” pozisyonlar görebileceğidir. Bu dış bakış açısıyla, cisim anlık olarak uzay boyunca seyahat edebilir. Bu tür durumlarda cismin mevcut uzaysal konumu kendi gelecek ışık konisinde bulunmayacağından, cisim hareket etmek zorundadır. Ek olarak, yeterli miktarda yana yatmayla, “geçmiş”te bulunan olay konumları dışarıdan görünebilir olacaktır. Kendisine uzay ekseni olarak görünen şeyin uygun bir hareketiyle, cisim dışarıdan bakıldığında zaman boyunca hareket ediyormuş gibi görünecektir.

Kapalı zamansı eğri, buna benzer ışık konilerinin kendileri üzerinden döngü oluşturaca şekilde bir araya getirilerek yaratılabilir, böylelilkle bir cismin bu döngü boyunca hareket edip sonra da harekete başladığı yere ve zamana dönmesi mümkün olacaktır. Böyle bir yörüngede bulunan cisim, serbest düşüşte bulunduğu sürece uzayzamanda tekrar tekrar aynı noktaya dönecektir. Orijinal uzayzaman konumuna dönmesi yalnızca bir ihtimaldir; cismin gelecek ışık konisine zamanda hem ileride hem de geride bulunan uzayzaman noktaları dahildir ve bu yüzden cismin bu koşullar altında zaman yolculuğu yapabilmesi ihtimaller dahilindedir.

Genel Rölativite

KZEler, genel rölativitenin konusu olan Einstein alan denklemlerinin yerel olarak itiraz edilemez kesin sonuçlarında karşımıza çıkar, bunlara en önemli çözümler de dahildir. Bunlar arasında:

Bu örneklerden Tipler silindiri gibi bazıları, daha ziyade yapaydır ancak Kerr çözümlerinin harici kısmının bir bakıma genel olduğu düşünülmektedir, bu yüzden de dahili kısmının KZEler barındırdığını öğrenmek umut kırıcı olmaktadır. Çoğu fizikçi bu tür çözümlerdeki KZElerin yapay olduğunu düşünmektedir.

Sonuçlar

KZElerin bir özelliği de önceki zamanlara bağlı zaman çizgileri açma ihtimalleridir ve böylelikle önceki bir sebeple bağlantısı geriye doğru takip edilemeyecek olayları da açmış olurlar. Genel olarak nedensellik, uzayzamandaki her bir olayın, her nihai koordinatındaki kendinden önce gelen sonuca bağlanmasına gerek duyar. Bu prensip, genel rölativitenin uzaysı Cauchy yüzeyinde bulunan bir evrenin tüm bilgisiyle, uzayzamanın geri kalanının tüm hallerinin bilinebileceğini söyleyen determinizmde kritiktir. Ancak KZElerde nedensellik parçalanır çünkü bir olay sebebiyle “aynı anda” gerçekleşebilir –bir anlamda olay kendi sebebi olabilir. Yalnızca geçmişin bilgisine dayanarak, bir şeyin KZEde varolarak uzayzamandaki diğer nesnelere müdahale edip edemeyeceğini anlamak mümkün değildir. Bu yüzden de bir KZE Cauchy ufkuyla ve uzayzamanda herhangi bir geçmiş zamanın bütün bilgisiyle bile tahmin edilemeyecek bir bölgeyle sonuçlanır.

Herhangi bir KZE, sürekli olarak KZE haliyle deforme edilemez (bunun anlamı bir KZE ve noktanın zamansı uzamdaş olmadığıdır), çünkü manifold bu noktada olağan haliyle uygun davranmayacaktır. KZEnin bir noktaya doğru deforme edilmesine engel olan topolojik özelliğinin adı zamansı topoloji özelliğidir.

KZElerin varlığı , evrendeki madde-enerji alanlarının fiziksel olarak izin verilebilir durumlarına engellemeler getirecektir. Kapalı zamansı zaman çizgileri ailesi boyunca alan konfigürasyonu yaymak, orijinalinin aynısı bir durumla sonuçlanmak zorundadır. Bu, bazı biliminsanlarınca KZElerinde var olmadığını kanıtlamak için bir yaklaşım olarak keşfedilmiştir. KZElerin varlığı aynı zamanda kuantum ve klasik hesaplama denkliklerinin de varlığını ima etmektedir (her ikisi de PSPACEte).[2]

Büzülebilir ve büzülemez

İki KZE sınıfı vardır. Bir noktaya büzülebilen KZEler vardır (eğer her yere doğru gelecek yönelimli zamansı olması noktasında ısrarcı değilsek) ve büzülebilir olmayan KZEler vardır. İkincisi için her zaman evrensel kapsam uzayına başvurabiliriz ve nedenselliği tekrar sağlayabiliriz. İlki içinse, bu tür bir prosedür mümkün değildir. Hiçbir kapalı zamansı eğri, zamansı eğriler boyunca uzanan zamansı topografi kullanılarak tek bir noktada büzülemez, zira bu nokta nedensel anlamda uygun davranmayacaktır.[1]

Cauchy ufku

Kronoloji kurallarına uymayan küme, KZElerin içinden geçtiği noktalar kümesidir. Bu kümenin sınırı ise Cauchy ufkudur. Cauchy ufku, kapalı boş jeodezikler tarafından oluşturulur. Her bir kapalı boş jeodezikle bağlantılı olan, ilgin parametrelerin döngü etrafındaki değişim hıznın yeniden ölçeklendirilmesini tanımlayan bir kızıl kayma faktörü mevcuttur. Bu kızıl kayma faktörü nedeniyle, ilgin parametreler, belli bir sayıda dönüşten sonra sonlu bir sayıda duracaktır çünkü geometrik seriler yakınsaktır.

Ayrıca bakınız

Notlar

  1. 1 2 H. Monroe (2008). "Are Causality Violations Undesirable?". Foundations of Physics 38 (11): 1065–1069. arXiv:gr-qc/0609054. Bibcode 2008FoPh...38.1065M. DOI:10.1007/s10701-008-9254-9.
  2. ↑ Watrous, John; Aaronson, Scott (2009). "Closed timelike curves make quantum and classical computing equivalent". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 465 (2102): 631. arXiv:0808.2669. Bibcode 2009RSPSA.465..631A. DOI:10.1098/rspa.2008.0350.

Referanslar

Dış linkler

This article is issued from Vikipedi - version of the 8/20/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.