Kerr metriği

Bu sayfa, başka dilde bir Vikipedi'den çevrilmektedir. Siz de yardım etmek istiyorsanız veya çeviri yarıda kalmışsa, çalışmaya katılan kişilerle veya çeviri grubu ile iletişime geçip, sayfanın durumunu onlara sorabilirsiniz. Sayfanın geçmişine baktığınızda, sayfa üzerinde çalışma yapanları görebilirsiniz.

Kerr metrik veya Kerr vakum küresel olay ufkunun ile dönen yüksüz eksenel simetrik kara deliğin etrafındaki boş uzay geometrisini açıklar. Kerr metrik genel görelilik Einstein alan denklemlerinin tam bir çözümdür; Bu denklemler son derece bulmak için kesin çözümler çok zor kılan doğrusal olmayan vardır. Kerr metrik 1916 yılında Karl Schwarzschild'le tarafından keşfedilen ve bir yüksüz, küresel-simetrik çevresindeki uzay geometrisini açıklar ve vücudu dönmeyen oldu Schwarzschild metrik, bir genelleme olduğunu. Bir ücret, küresel, dönmeyen vücut için gelen çözüm, Reissner-Nordström metrik, kısa bir süre sonra (1916-1918) keşfedildi. Roy Kerr tarafından keşfedildi Ancak, bir yüksüz, dönen kara delik, Kerr metrik için kesin çözüm, 1963 yılına kadar faili meçhul kalmıştır. Bir ücret, dönen kara delik doğal uzantısı, Kerr-Newman metrik, kısa bir süre sonra 1965 yılında bu dört benzer çözümler aşağıdaki tabloda özetlenmiştir olabilir keşfedildi:

	Non-rotating (J = 0)	Rotating (J ≠ 0)
Uncharged (Q = 0)	Schwarzschild	Kerr
Charged (Q ≠ 0)	Reissner–Nordström	Kerr–Newman

Bu tabloda Q elektrik yükünü gösterirken, J açısal momentumu simgelemektedir.

Kerr metrik göre, örneğin dönen kara delikler çerçeve sürükleyerek, genel görelilik alışılmadık bir tahmin göstermelidir. Bu çerçeve sürükleme etkisinin ölçülmesi Yerçekimi Probe B deney önemli bir gol oldu. Kabaca söylemek gerekirse, bu etkinin dönen kitle yakın gelen nesneler herhangi ziyade çünkü dönen organları ile ilişkili uzay-zamanın eğriliği, kuvvet veya hissedilebilir tork uygulanmaz çünkü, onun dönme katılmaya sürüklenen olacağını tahmin ediyor. Yeterince yakın mesafelerde, tüm nesneleri - hatta kendini yakmak - kara delik ile dönmelidir; Bu tutar bölge ergosphere olarak adlandırılır.

Döner kara delikler metrik bir tekillik gibi görünüyor yüzeyleri; Bu yüzeylerin büyüklüğü ve şekli kara deliğin kütlesi ve açısal momentum bağlıdır. Dış yüzey ergosphere çevreler ve düzleştirilmiş bir küre benzer bir şekle sahiptir. Iç yüzeyi de "olay ufku" olarak adlandırılan "dönüşü yarıçapını" işaretleri; Bu yarıçap geçen nesneleri tekrar yarıçapı dış dünya ile iletişim asla. Açıkça görülen tekillik farklı koordinat sisteminde elimine edilebilir Bununla birlikte, ne yüzey gerçek tekillik vardır. Bu iki ufuk arasında Nesneler-co döndürmek yukarıda belirtildiği gibi, döner gövde ile zorundadır; Bu özelliği değişmez kütle enerji, MC2 kadar, dönen bir kara delik enerji ayıklamak için kullanılır.

Matematiksel Formülü

Kerr metriği^[1][2] M kütlelili, J açısal momentumlu cismin uzay zaman geometrisini tanımlar

   

${\displaystyle {\begin{aligned}c^{2}d\tau ^{2}=&\left(1-{\frac {r_{s}r}{\rho ^{2}}}\right)c^{2}dt^{2}-{\frac {\rho ^{2}}{\Delta }}dr^{2}-\rho ^{2}d\theta ^{2}\\&-\left(r^{2}+\alpha ^{2}+{\frac {r_{s}r\alpha ^{2}}{\rho ^{2}}}\sin ^{2}\theta \right)\sin ^{2}\theta \ d\phi ^{2}+{\frac {2r_{s}r\alpha \sin ^{2}\theta }{\rho ^{2}}}\,c\,dt\,d\phi \end{aligned}}}$

(1)

   

Kordinatlar, silindirik kordinat sistemi için ${\displaystyle r,\theta ,\phi }$ ve r_s Schwarzschild yarıçapı iken.

   

${\displaystyle r_{s}={\frac {2GM}{c^{2}}}}$

(2)

   

ve α, ρ, Δ uzunlukları kısalılarıyla bilinirken

   

${\displaystyle \alpha ={\frac {J}{Mc}}}$

(3)

   

   

${\displaystyle \rho ^{2}=r^{2}+\alpha ^{2}\cos ^{2}\theta }$

(4)

   

   

${\displaystyle \Delta =r^{2}-r_{s}r+\alpha ^{2}}$

(5)

   

Göreceli olmayan limitte M (veya ona bağlı olarak r_s) sıfıra giderken, Kerr metriği orthogonal metrik olur oblate silindirik kordinatlariçin.

   

${\displaystyle c^{2}d\tau ^{2}=c^{2}dt^{2}-{\frac {\rho ^{2}}{r^{2}+\alpha ^{2}}}dr^{2}-\rho ^{2}d\theta ^{2}-\left(r^{2}+\alpha ^{2}\right)\sin ^{2}\theta d\phi ^{2}}$

(6)

   

Bu da Boyer–Lindquist kordinatlarına^[3] eşittir

   

${\displaystyle {x}={\sqrt {r^{2}+\alpha ^{2}}}\sin \theta \cos \phi }$

(7)

   

   

${\displaystyle {z}=r\cos \theta }$

(9)

   

Dalga islemcisi

Kerr metrikte doğrudan kontrol hantal hesaplamalar içerdiğinden, metrik tensörün kontravaryant bileşeni Dört-gradyan operatöründe ${\displaystyle g^{ik}}$ aşağıda gösterildiği gibidir:

   

${\displaystyle {\begin{aligned}g^{\mu \nu }{\frac {\partial }{\partial {x^{\mu }}}}{\frac {\partial }{\partial {x^{\nu }}}}=&{\frac {1}{c^{2}\Delta }}\left(r^{2}+\alpha ^{2}+{\frac {r_{s}r\alpha ^{2}}{\rho ^{2}}}\sin ^{2}\theta \right)\left({\frac {\partial }{\partial {t}}}\right)^{2}+{\frac {2r_{s}r\alpha }{c\rho ^{2}\Delta }}{\frac {\partial }{\partial {\phi }}}{\frac {\partial }{\partial {t}}}\\&-{\frac {1}{\Delta \sin ^{2}\theta }}\left(1-{\frac {r_{s}r}{\rho ^{2}}}\right)\left({\frac {\partial }{\partial {\phi }}}\right)^{2}-{\frac {\Delta }{\rho ^{2}}}\left({\frac {\partial }{\partial {r}}}\right)^{2}-{\frac {1}{\rho ^{2}}}\left({\frac {\partial }{\partial {\theta }}}\right)^{2}\end{aligned}}}$

(10)

   

Frame dragging

Kerr metriği aşağıda gösterildiği gibi yazabiliriz (1):

   

${\displaystyle c^{2}d\tau ^{2}=\left(g_{tt}-{\frac {g_{t\phi }^{2}}{g_{\phi \phi }}}\right)dt^{2}+g_{rr}dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi }\left(d\phi +{\frac {g_{t\phi }}{g_{\phi \phi }}}dt\right)^{2}.}$

(11)

   

Metrik eş-dönen Ω açısal hızlı referans sisteminin eşleniğidir ve bu açısal hız hem yarı çap r'ye hem de colatitude θ ya bağlıdır, Ω öldüren ufuk iken.

   

${\displaystyle \Omega =-{\frac {g_{t\phi }}{g_{\phi \phi }}}={\frac {r_{s}r\alpha c}{\rho ^{2}\left(r^{2}+\alpha ^{2}\right)+r_{s}r\alpha ^{2}\sin ^{2}\theta }}.}$

(12)

   

Böylece, bir eylemsiz referans çerçevesi sonrakinin dönme katılmak için dönen merkezi kütlesi ile karışır; Bu çerçeve sürükleyerek denir, ve deneysel olarak test edilmiştir. [4] Nitel, çerçeve sürükleme elektromanyetik indüksiyon yerçekimi analog olarak görülebilir. Bir "buz patenci", ekvator üzerinde yörüngede ve dönerek yıldızlara göre dinlenme, kollarını uzatır. Kara deliğe doğru uzatılmış kol dönme yönüne torqued edilecektir. Kara delikten uzak genişletilmiş kol, anti-dönme yönüne torqued edilecektir. O nedenle dönerek kara deliğe bir ters yönde dönen anlamda, hızlandırdı olacak. Bu gündelik deneyim ne tersidir. O kollarını, atalet etkileri ve çerçeve sürükleyerek etkilerini uzandığında o zaten belli bir hızda dönen ise dengeler ve onun sıkma değişmez. Denklik Prensibi nedeniyle yerçekimi etkileri atalet etkilerinden yerel ayırt edilemez, bu yüzden olur kollarını şey uzandığı bu dönme oranı, sigara rotasyon için onu yerel bir referanstır. Bu çerçeve, sabit yıldızlar ve sayaç dönen karadelik ile ilgili ile ilgili dönüyor. Yararlı bir metafor kara delik güneş dişlisi, bir planet dişli ve dişli halka olmanın dışında evren buz patenci olmak bir planet dişli sistemi. Bu da Mach prensibi ile yorumlanabilir olabilir.

The two surfaces on which the Kerr metric appears to have singularities; the inner surface is the spherical event horizon, whereas the outer surface is an oblate spheroid. The ergosphere lies between these two surfaces; within this volume, the purely temporal component g_tt is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character.

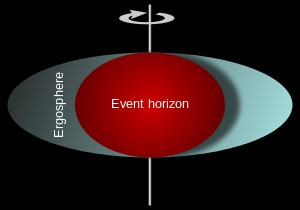
Önemli yüzeyler

Kerr mt tekil olarak görünen iki fiziksel uygun yüzeylere sahiptir. Iç yüzey Schwarzschild metrik gözlenene benzer bir olay ufuk tekabül etmektedir; Bu metriğin g_rr limiti sıfıra giderken gerçekleşir. Quadratik denklemi 1/g_rr = 0 ile çözmek sağlamaktadır.

${\displaystyle r_{\mathit {inner}}={\frac {r_{s}+{\sqrt {r_{s}^{2}-4\alpha ^{2}}}}{2}}}$

Bir başka tekillik sadece g_tt bileşeni pozitiften negatife işaret değiştirirken meydana gelir. Yeniden quadratik denklemi g_tt=0 ile çözmek denklemi sağlar:

${\displaystyle r_{\mathit {outer}}={\frac {r_{s}+{\sqrt {r_{s}^{2}-4\alpha ^{2}\cos ^{2}\theta }}}{2}}}$

Karekok icindeki cos2θ li ifadeden dolayi, dis yuzey θ nin 0 veya π esit oldugu ic yuzeye dokunan basik bir kureye benzer ve bu yuzeylere ergosfer denir. Bu ikinci derece denklerimlerin iki fark cozumu daha vardir ama cozumler olay ufku icerisinde bulunur ve oralarda Kerr metrigi kullanilmaz bundan dolayi soyuttur.

Hareketli parçacık kendi dünyaçizgisinin, uzay yoluyla yol boyunca olumlu uygun bir zaman yaşar. Parçacık Ω en az bir açısal hız ile iç kütle M ile birlikte dönen sürece Bununla birlikte, bu, GTT negatiftir ergosphere içinde mümkün değildir. Böylece, hiçbir parçacık ergosphere içinde merkez kitle tersini döndürebilirsiniz

Schwarzschild metrik olay ufkunun gibi Rinner ve yönlendirici belirgin tekillik koordinatlar (yani, onlar tekillik koordinat) seçimi yarattığı bir illüzyon. Aslında, uzay-zaman sorunsuz koordinatları uygun seçimi ile içlerinden devam edilebilir.

Ergosfer ve Penrose süreci

Genel olarak bir kara delik bir yüzey ile çevrilidir, olay ufku denir ve kaçış hızı ışık hızına eşit dönmeyen kara delik için Schwarzschild yarıçapı yer. Bu yüzeyin içinde, hiçbir gözlemci / parçacık sabit yarıçaplı kendini muhafaza edebilir. Bu içe düşmeye zorlanır ve böylece bu bazen statik sınırı denir.

Dönen kara delik olay ufkunda aynı statik limite sahiptir ama "ergosurface" olay ufkunun dışında ${\displaystyle (r-GM)^{2}=G^{2}M^{2}-J^{2}\cos ^{2}\theta }$ ile verilen başka bir yüzey daha vardır Boyer–Lindquist cordinatlarında, bu da çevreleyen uzayın rotasyonel hızın ışık hızına eşit olduğu küre ile karakterize edilebilir. Bu alanı içinde sürükleme ışık hızından daha büyüktür, ve herhangi bir gözlemci / parçacık co-döndürmek zorunda kalır.

Olay ufkunun dışında ancak dönme hızı ışık hızıdır iç yüzeyinde bölge, (Yunanca ergon anlam işten) ergosphere denir. Ergosphere giren Parçacıklar daha hızlı döndürmek ve böylece enerji kazanmak zorunda. Onlar olay ufkunun dışında hala Çünkü, onlar kara delik çıkabilir. Net bir süreç dönen kara delik kendi toplam enerjinin pahasına enerjik parçacıklar yayar olmasıdır. Dönen kara delik spin enerji çıkarma olasılığı ilk 1969 yılında matematikçi Roger Penrose tarafından önerilen ve böylece Penrose süreci denir. Astrofizik Döner kara delikler enerji büyük miktarda bir potansiyel kaynağıdır ve gama ışını patlamaları gibi enerjik fenomeni açıklamak için kullanılır.

Kerr vakumun özellikleri

Kerr vakumu birçok önemli özelliği sergiler: azami analitik uzantısı asimptotik düz dış bölgelerin sekansı, bir ergosfere sabit sınır yüzeyleri, etkinlik diliminde, auchy ufuklar, ilişkili her bir kapalı zamansal eğriler ve halka şeklinde bir kavis tekilliği içerir. Jeodezik denklemi kapalı formda tam çözülebilir. İki The Killing vektör alanlara (zaman çeviri ve Eksenel simetri karşılık gelir) yanı sıra, Kerr vakum olağanüstü Killing tensörünü itiraf ediyor. Asıl boş kongrüansları (bir hava parası ve bir giden) bir çift vardır. Weyl tensör aslında küresel yapı bilinen Petrov tipi D. vardır, cebirsel özeldir. Topolojik, Kerr uzay-zamanın homotopi tipi basitçe her tamsayı noktasında bağlı çevrelerin bir çizgi olarak karakterize edilebilir.

Kerr vakum iç bölgede tedirginlikler açısından kararsız olduğunu unutmayın. Bu istikrarsızlık Kerr metrik eksen-simetrik olmasına rağmen yerçekimsel çöküş aracılığıyla oluşturulan bir kara delik o kadar olmayabilir gelir. Bu istikrarsızlık da yukarıda açıklanan Kerr vakum özellikleri birçok da muhtemelen böyle bir kara delik mevcut olmayacağını ima eder.

Işık bir kara delik yörünge hangi A yüzey foton küre denir. Kerr çözümü bir iç ve bir dış bir biri arasında yatan, sonsuz sayıda foton alanı mevcuttur. Tüm fotonlar küre aynı yarıçap meydana böylece α = 0 ile dönmeyen, Schwarzschild çözümü, ise, iç ve dış foton küreler, dejenere. Kara deliğin büyük sıkma uzak iç ve dış foton küreler taşımak birbirinden vardır. Kara deliğin spin ters yönde hafif hareket demeti dairesel bir dış foton küre ile delik yörünge olacak. Kara deliğin döndürme aynı yönde ışık hareket demeti olacak iç foton kürenin de dairesel yörüngeye. Dik kara deliğin dönme eksenine bazı açısal momentum ile jeodezikler yörüngede bu iki uç arasındaki foton küreler üzerinde yörüngeye olacaktır. Uzay-zaman dönen Çünkü \ phi \ bir kayma olduğundan, bu tür yörüngeler, bir sapmasının çözümlenebilir sergileyen, değişken \ teta \ bir dönem, değişken tamamladıktan sonra.

Overextreme Kerr solutions

The location of the event horizon is determined by the larger root of ${\displaystyle \Delta =0}$. When ${\displaystyle {r_{s}/2}<\alpha }$ (i.e. ${\displaystyle GM^{2}<Jc}$), there are no (real valued) solutions to this equation, and there is no event horizon. With no event horizons to hide it from the rest of the universe, the black hole ceases to be a black hole and will instead be a naked singularity.^[4]

Solucan deliği olarak Kerr kara delikleri

Şablon:Refimprove section

Kerr çözümü bu yeni koordinatlar uygun bir seçim ile, aslında tekillik koordine ve, Δ = 0 köklerine tekil olarak görünse de, Kerr çözümü sorunsuz bu köklerine tekabül r değerleri ile uzatılabilir. Bu köklerin büyük olay ufkunun yerini belirler, ve küçük bir Cauchy ufkunun konumunu belirler. Bir (gelecek yönelimli, zaman gibi) eğrisi dış başlayacak ve olay ufkunun içinden geçebilir. Bir kez olay ufkunun içinden geçtikten r şimdi koordinat zaman gibi davranır koordinat, yani eğri Cauchy ufkunun geçer kadar azaltmak gerekir.

Cauchy ufkunun ötesinde bölge birkaç şaşırtıcı özelliklere sahiptir. Uzamsal koordinat ve serbestçe değişebilir gibi yeniden r koordinat davranır. Bir (gelecek yönelimli bir zaman gibi) eğrisi ikinci olay ufkunun içinden, ikinci bir Cauchy ufkunun boyunca devam simetrik yolu boyunca devam edebilir, böylece iç bölge, ve dışarı yeni bir dış bölgeye, bir yansıma simetrisi vardır Kerr çözümünün orijinal dış bölgeye izometrik. Eğri ardından yeni bölgede sonsuza kaçmak ya da yeni dış bölgenin gelecekteki olay ufkunu girin ve işlemi tekrarlayın olabilir. Bu ikinci dış bazen başka bir evrene olarak düşünülür. Öte yandan, Kerr, çözelti içinde, tekillik bir halka olduğu, ve eğri bu halka merkezi içinden geçebilmektedir. Izni dışında bölge süresi gibi eğrileri kapalı. Gözlemci ve genel görelilik parçacıkların yörünge süresi gibi eğriler tarafından açıklanan beri bu bölgede gözlemciler kendi geçmişe dönmek için, bu mümkün.

O Kerr çözümünün dış bölge kararlı olduğunu, ve sonunda bir Kerr metrik yaklaşım tüm dönen kara delikler, çözümün iç bölge çok kendi noktada dengeli bir kalem gibi, kararsız olması göründüğünü beklenirken. [5 ] Bu kozmik sansür fikrine ilgilidir.^[5]

Diğer kesin sonuçlarla olan ilişkisi

Kerr vakum Einstein alan denkleme sabit bir eksenel simetrik vakum çözeltisi özel bir örnek. Einstein alan denkleminin tüm sabit eksenel simetrik vakum çözümleri ailesi Ernst vakumlar vardır. Kerr çözümü de hangi modeli kara delikler çeşitli sivil vakum çözümleri ile ilgilidir. Örneğin, Kerr-Newman Elektro modelleri elektrik yüküne sahip bir (dönen) kara delik, infalling elektromanyetik radyasyon ile Kerr-Vaidya boş toz modelleri ise bir (dönen) delik. Kerr metrik özel durum \ alfa = 0 \, Schwarzschild'le statik ve küresel simetrik bir dönmeyen kara delik, koordinatları modelleri Schwarzschild metrik, verir. (Bu durumda, her Geroch an ancak kitlesel kaybolur). Kerr vakum, daha doğrusu onun bir kısmının iç, Chandrasekhar-Ferrari CPW vakum, bir çarpışan düzlem dalga modelinin bir örneği izometrik yerel. Bu CPW çözümün küresel yapı Kerr vakum o oldukça farklı ve prensipte, bir deneyci çarpışmasını düzenleyerek Kerr iç (dış kısmının) geometrisini incelemek için umut olabilir, çünkü bu, özellikle ilginçtir iki uygun yerçekimsel dalgalar düzlem.

Çok kutuplu anlar

Her asimptotik düz Ernst vakum göreli kutuplu anları sonsuz dizisini vererek karakterize edilebilir, ilk iki kütle ve alanın kaynağının açısal momentum olarak yorumlanabilir. Birbirleri ile anlaşmak için söndürmeden nedeniyle Hansen, Thorne ve Geroch göresel çok kutuplu anlar, alternatif formülasyonlar bulunmaktadır. Hansen tarafından hesaplanmıştır Kerr vakum göreli kutuplu anları; onlar çıkmak

${\displaystyle M_{n}=M\,(i\,\alpha )^{n}}$

Bu sebeple, Schwarzschild vakum (α = 0) özel durum genel görelilik "monopol noktası kaynağı" verir.

Uyarı: kullanan tüm sabit eksenel simetrik vakumlar çözümleri Ernst ailesi için Weyl-Papapetrou grafik görünen (resmen Newtoncu yerçekimi potansiyeli karşılık gelen) belli bir metrik fonksiyon tedavi kaynaklanan Weyl çok kutuplu anlar, bu rölativistik kutuplu anları karıştırmayın standart Öklid skaler kutuplu anlar. Bir anlamda, Weyl anlar yalnızca (dolaylı) izole kaynağın "kitle dağılımı" karakterize, ve sadece bile sipariş göreli anları bağlı çıkmak. Çözeltiler halinde ekvator düzlemi boyunca Weyl anlar ortadan tek düzeni simetrik. Kerr vakum çözümleri için, ilk birkaç Weyl anları tarafından verilmektedir

${\displaystyle a_{0}=M,\;\;a_{1}=0,\;\;a_{2}=M\,\left({\frac {M^{2}}{3}}-\alpha ^{2}\right)}$

Özellikle, biz Schwarzschild vakum "Weyl monopol" belli bir sonlu Newton potansiyeli doğar Chazy-Curzon vakum çözüm değil, Schwarzschild vakum çözümü olduğunu gerçeğine karşılık, sıfırdan farklı ikinci dereceden Weyl anı olduğunu görmek uzunluk üniforma yoğunluğu ince çubuk.

Zayıf alan genel görelilik olarak, sırasıyla kütle ve kaynak momentum dağılımını karakterize eden kitle kutuplu anlar ve momentum kutuplu anlar Weyl anlar genelleştirmek çok kutuplu bir başka türünü kullanarak izole kaynakları, tedavi uygundur. Bunlar, uygun simetriklestirilir (anti-simetriklestirilir) parçalar oldukça karmaşık bir şekilde tam doğrusal olmayan teoriye relativistik anları gerçek ve hayali parçaları ile ilgili olabilir çok endeksli miktarları vardır.

Perez ve Moreschi r (radyal Weyl-Papapetrou grafikte koordinat) yetkilerinin Ernst vakumlar standart NP tetrad genişleterek "monopol çözümleri" bir alternatif kavramını verdik. Bu formülasyona göre:

• the isolated mass monopole source with zero angular momentum is the Schwarzschild vacuum family (one parameter),
• the isolated mass monopole source with radial angular momentum is the Taub–NUT vacuum family (two parameters; not quite asymptotically flat),
• the isolated mass monopole source with axial angular momentum is the Kerr vacuum family (two parameters).

In this sense, the Kerr vacuums are the simplest stationary axisymmetric asymptotically flat vacuum solutions in general relativity.

Açık problemler

Kerr vakum genellikle bir kara delik bir model olarak kullanılır, ama biz çözüm tutarsan ilke biz modellemek için bir dış çözüm olarak kullanmak gerekir, sadece bazı kompakt bölge (bazı kısıtlamalara tabi) dışında geçerli olmak üzere böyle bir nötron yıldızı ya da Dünya'ya gibi bir kara delik, başka bir dönen büyük nesnenin etrafında çekim alanı. Bu, gerçekten daha genel statik küresel simetrik mükemmel sıvı çözümler bir Schwarzschild sıvı iç Schwarzschild vakum dış maç ve olabilir dönmeyen durumda, çok güzel çalışır. Ancak, Kerr dış eşleştirilmiş olabilir dönen mükemmel sıvı içini bulma sorunu, ya da gerçekten herhangi bir asimptotik düz vakum dış çözüm, çok zor kanıtlanmıştır. Özellikle, bir kez düşünülen Wahlquist sıvı, bir Kerr dış eşleşen bir aday, şimdi böyle bir eşleştirme itiraf değil bilinmektedir olmak. Şu anda sadece yaklaşık çözümler modelleme yavaş yavaş dönen akışkan topları bilinen görünüyor. (Yavaşça sıvı topları sıfırdan farklı kütle ve açısal momentum, ancak daha yüksek kutuplu anları kaybolan ile basık küresel topları göreli analog olan döner.) Yalnız Neugebauer–Meinel diskin dışı, Kerr vacuumum sınırlı durumlarında, dönen diski örnek alan toz çözümüne sahiptir

Trajectory equations

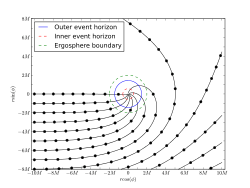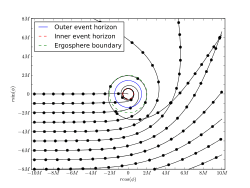Particle trajectories in the plane ${\displaystyle \theta =\pi /2}$ around a clockwise (left) and counter-clockwise (right) rotating black hole. The black hole has mass ${\displaystyle M}$ and ${\displaystyle \alpha =\pm 0.9}$. The coordinates in the plots are ${\displaystyle (\cos(\phi )r,\sin(\phi )r)}$. The dots are separated by a proper time of ${\displaystyle M}$. The particles all start with only horizontal velocity at ${\displaystyle \cos(\phi )r=-10M}$. All particles have conserved energy ${\displaystyle E=1}$. This is the energy per unit mass the particles had infinitely far away from the black hole. Units such that ${\displaystyle c=1,\ G=1}$ have been used.

Aşağıdaki gibi yörünge ve Kerr alanında bir parçacığın zaman bağımlılığı denklemleri vardır.

Hamilton-Jacobi denklemi biz formda eylem S yazarsak:

${\displaystyle \ S=-E_{0}t+L\phi +S_{r}(r)+S_{\theta }(\theta )}$

${\displaystyle E_{0}}$, m, ve L korunan enerji iken geri kalan kütle ve parçacığın açısal momentum bileşenleri (alanın simetri ekseniyle birlikte) aşağıdaki şekilde incelenir:

${\displaystyle \left({\frac {dS_{\theta }}{d\theta }}\right)^{2}+\left(\alpha E_{0}\sin \theta -{\frac {L}{\sin \theta }}\right)^{2}+\alpha ^{2}m^{2}\cos ^{2}\theta =K}$

${\displaystyle \Delta \left({\frac {dS_{r}}{dr}}\right)^{2}-{\frac {1}{\Delta }}\left[\left(r^{2}+\alpha ^{2}\right)E_{0}-\alpha L\right]^{2}+m^{2}r^{2}=-K}$

K dördüncü fourth isteğe bağlı sabit iken (genellikle Carter sabiti olarak adlandırılır). yolun denklemi ve zamana bağlı kordinatlar yol la beraber (hareket denklemi) bu denklemlerden kolaylıkla bulunabilir:

${\displaystyle {\frac {\partial {S}}{\partial {E_{0}}}}=const}$

${\displaystyle {\frac {\partial {S}}{\partial {L}}}=const}$

${\displaystyle {\frac {\partial {S}}{\partial {K}}}=const}$

Simetriler

Kerr metrik izometrileri grup kendisine tekillik iki-boyutlu odağına alır on-boyutlu Poincare grubunun alt grubu olan. Bu dönme (tek boyut) kendi ekseni etrafında zaman çeviriler (tek boyut) ve rotasyonları korur. Böylece iki boyutu vardır. Poincare grubu gibi, bu dört bağlı bileşeni vardır: kimlik bileşeni; zaman ve boylam ters bileşen; ekvatoral düzlem boyunca yansıtır bileşen; ve bileşen hem de yaptığı.

Fizikte, simetriler genellikle Noether teoremi doğrultusunda hareket korunmuş sabitleri ile ilişkilidir. Yukarıda gösterildiği gibi, jeodezik denklemleri dört korunmuş miktarlarda vardır: bunlardan biri bir jeodezik tanımı gelmektedir ve iki Kerr geometrisinin saat için ve dönme simetri ortaya çıkmaktadır. Dördüncü korunmuş miktarı, standart anlamda bir simetri ortaya çıkmaz ve yaygın olarak gizli bir simetri olarak adlandırılır.

Ayrıca bakınız

• Schwarzschild metriği
• Kerr–Newman metriği
• Reissner–Nordström metriği
• Spin-flip
• Kerr–Schild spacetime

1. Kerr, Roy P. (1963). "Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics". Physical Review Letters 11 (5): 237–238. Bibcode 1963PhRvL..11..237K. DOI:10.1103/PhysRevLett.11.237. http://prola.aps.org/abstract/PRL/v11/i5/p237_1. 
2. Landau, L. D.; Lifshitz, E. M. (1975). The Classical Theory of Fields (Course of Theoretical Physics, Vol. 2) (revised 4th English bas.). New York: Pergamon Press. s. 321–330. ISBN 978-0-08-018176-9. 
3. Boyer, Robert H.; Lindquist, Richard W. (1967). "Maximal Analytic Extension of the Kerr Metric". J. Math. Phys. 8 (2): 265–281. Bibcode 1967JMP.....8..265B. DOI:10.1063/1.1705193. 
4. Chandrasekhar, S. (1983). The Mathematical Theory of Black Holes. International Series of Monographs on Physics. 69. s. 375. 
5. Penrose 1968