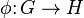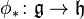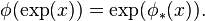Lie grubu homomorfizması
Matematikte, bir Lie grup homomorfizmaları Lie grupları arasında bir haritadır
Hem bir grup homomorfizması ve hem de bir pürüzsüz bir haritadır. Lie grubu eşyapıları Lie gruplarının kategorisinde morfizmler vardır.Karmaşık Lie grupları durumunda , holomorfik fonksiyonlar bir doğal homomorfizmalar olmayı gerektirir .Gerçek ya da kompleks durumunda,aslında yalnızca haritaları sürekli olması için gerekli ve yeterlidir. Lie gruplar arasında her sürekli homomorfizması bir analitik fonksiyon olarak ortaya çıkıyor .
Lie gruplarının bir izomorfizması olan ayrıca bir homomorfizma ve tersi de bir homomorfizmadır.Eşdeğeri,aynı zamanda bir grup homomorfizmaları bir difeomorfizm(eğribiçim)dir.
Diyelimki 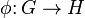 Bir Lie grup homomorfizması ve diyelimki
Bir Lie grup homomorfizması ve diyelimki 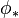 kimliği onun türevi olsun. Eğer Biz kimlik onların tanjant uzayları ile G ve H Lie cebirlerinin özdeşliği varsa ve bu
kimliği onun türevi olsun. Eğer Biz kimlik onların tanjant uzayları ile G ve H Lie cebirlerinin özdeşliği varsa ve bu 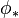 ise karşılık gelen Lie cebiri ve bir harita arasında:
ise karşılık gelen Lie cebiri ve bir harita arasında:
Bir 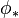 (aslında o Lie braketini koruyan bir doğrusal harita anlamına gelir) bir Lie cebiri homomorfizması gösterebilir.Kategori teorisi dilinde,Lie grupları kategorisinden Lie cebiri kategorisine bir Lie cebirine bir eşdeğişir funktör ve bir Lie grup homomorfizminin onun özdeş türevine gönderilen bir Lie grubudur
Lie grubu homomorfizmalarının en önemli özelliklerinden biri haritalar
(aslında o Lie braketini koruyan bir doğrusal harita anlamına gelir) bir Lie cebiri homomorfizması gösterebilir.Kategori teorisi dilinde,Lie grupları kategorisinden Lie cebiri kategorisine bir Lie cebirine bir eşdeğişir funktör ve bir Lie grup homomorfizminin onun özdeş türevine gönderilen bir Lie grubudur
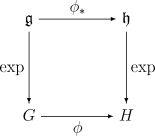
Lie grubu homomorfizmalarının en önemli özelliklerinden biri haritalar 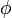 ve
ve 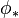 üstel harita ile ilgili olmasıdır.Elimizdeki tüm
üstel harita ile ilgili olmasıdır.Elimizdeki tüm 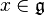 için
için
Diğer bir deyişle aşağıdaki diyagram sırabağımsızdır: