Pareto dağılımı

Pareto

Olasılık yoğunluk fonksiyonu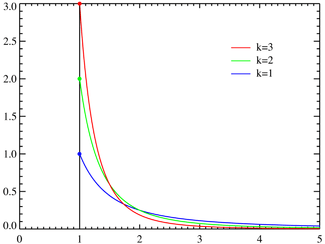 xm = 1 oldugu halde çeşitli k değerleri için Pareto olasılık yoğunluk fonksiyonları. Yatay eksen x parametredir. Limitte k → ∞, dağılım δ(x - xm) yaklaşır; burada δ Dirac delta fonksiyonudur.
Yığmalı dağılım fonksiyonu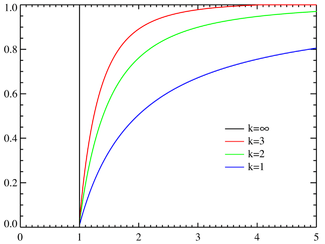 xm = 1 oldugu halde çeşitli k değerleri icin Pareto yığmalı dağılım fonksiyonları. Yatay eksen x parametredir.
Parametreler	${\displaystyle x_{\mathrm {m} }>0\,}$ ölçek (reel) ${\displaystyle k>0\,}$ shape (reel)
Destek	${\displaystyle x\in [x_{\mathrm {m} };+\infty )\!}$
Olasılık yoğunluk fonksiyonu (OYF)	{{{OYF}}}
Yığmalı dağılım fonksiyonu (YDF)	{{{YDF}}}
Ortalama	${\displaystyle {\frac {k\,x_{\mathrm {m} }}{k-1}}\!}$ for ${\displaystyle k>1}$
Medyan	${\displaystyle x_{\mathrm {m} }{\sqrt[{k}]{2}}}$
Mod	${\displaystyle x_{\mathrm {m} }\,}$
Varyans	${\displaystyle {\frac {x_{\mathrm {m} }^{2}k}{(k-1)^{2}(k-2)}}\!}$ ${\displaystyle k>2}$ icin
Çarpıklık	${\displaystyle {\frac {2(1+k)}{k-3}}\,{\sqrt {\frac {k-2}{k}}}\!}$ ${\displaystyle k>3}$ icin
Fazladan basıklık	${\displaystyle {\frac {6(k^{3}+k^{2}-6k-2)}{k(k-3)(k-4)}}\!}$ ${\displaystyle k>4}$ icin
Entropi	${\displaystyle \ln \left({\frac {k}{x_{\mathrm {m} }}}\right)-{\frac {1}{k}}-1\!}$
Moment üreten fonksiyon (mf)	tanımlanmaz; ham momentler icin metine bakın
Karakteristik fonksiyon	${\displaystyle k(-ix_{\mathrm {m} }t)^{k}\Gamma (-k,-ix_{\mathrm {m} }t)\,}$

Olasılık kuramı ve istatistik bilim dallarında Pareto dağılımı birçok pratik uygulaması bulunan ve "küçük" bir nesnenin bir "büyük" nesneye dağılımında kararlılık elde edildiği hallerde kullanılan bir sürekli olasılık dağılımı veya bir güç kuramıdır. İlk olarak bir İtalyan iktisatçısı olan Vilfredo Pareto tarafından ekonomilerde bireylerin servet dağılımını göstermek için kullanılmıştır. İktisat bilim dalı dışında bu dağılım Bradford dağılımı adı altında da bilinmektedir.

Uygulama alanları

Pareto dağılımı iktisat dışında, sosyal bilimler, fen, geofizik, sigortacılık ve birçok gözümlenen doal fonomen incelemeleri için geniş bir alanda uygulanabilimektedir.

• İktisatta, Wilfredo Pareto'nun ilk defa gösterdiği gibi, herhangi bir ülke veya idarî birim içinde servetin veya gelirin büyük bir kısmının incelenen sosyetenin küçük bir bireyler grubu tarafından sahip olunduğunu bu dağılım çok bariz bir şekilde göstermektedir. Bu öneri biraz daha az bilimsel olarak bazan Pareto prensipi veya 80-20 ilkesi olarak açıklanmakta ve bir ülkenin nüfusunun %20si, servetin veya gelirin %80ine sahip olduğu bu şekilde ifade edilmektedir.
• Tek hisse senedi için standardize edilmiş fiyat getirileri dağılımı.
• İçinde çok büyük sayıda sözcük bulunan ve bazı sözcükler çok tekrarlanırken diğer sözcüklerin nadir olarak kullanıldığı uzun metinlerde sözcük uzunluğu dağılımı.
• Değişik dillerde ve ülkelerde insanlara verilmiş olan isimlerin çokluluk dağılımları.
• TCP protokolunu kullanan İnternet trafiği için dosya büyüklüğü dağılımı.
• Mutlak sıfır yakınında Bose-Einstein yoğunlaşmaları grupları.
• Kum parçacıklarının büyüklük dağılımları.
• Metoritlerin büyüklük dağılımları.
• Orman yangınlarında yanan alanların yüzölçüm dağılımları.

Özellikler

Tanınım

Eğer X bir Pareto dağılım gösteren rassal değişken ise, Xin olasılığının değerini herhangi bir reel sayı olan xden daha büyük olması, yani tüm x ≥ x_m için, şu ifade ile verilir:

${\displaystyle \Pr(X>x)=\left({\frac {x}{x_{\mathrm {m} }}}\right)^{-k}}$

Burada x_m mutlaka X için verilen en küçük sayı değeri ve k ise pozitif değerde bir parametredir.

Pareto dağılımları ailesinin tanımlanması için iki tane sayısal parametre gerekmektedir:

x_m ve k.

Pareto dağılımı iktisatda servet veya gelir dağılımı modelinde kullanildigi zaman k parametresi Pareto endeksi olarak adlandırılır.

Olasılık yoğunluk fonksiyonu

Bu tanınımdan hemen şu Pareto dağılımı için olasılık yoğunluk fonksiyonu ortaya çıkartılır:

${\displaystyle f(x;k,x_{\mathrm {m} })=k\,{\frac {x_{\mathrm {m} }^{k}}{x^{k+1}}}\ {\mbox{for}}\ x\geq x_{\mathrm {m} }.\,}$

Diğer özellikler

• Pareto dağılımı gösteren bir rassal değişken için beklenen değer şöyle ifade edilir:

${\displaystyle E(X)={\frac {kx_{\mathrm {m} }}{k-1}}\,}$

Eğer k ≤ 1 ise beklenen değer sonsuz olacaktır.

• Varyans şöyle ifade edilir:

${\displaystyle \mathrm {var} (X)=\left({\frac {x_{\mathrm {m} }}{k-1}}\right)^{2}{\frac {k}{k-2}}.}$

Eğer ${\displaystyle k\leq 2}$ ise, varyans sonsuzdur.

• Ham momentler şöyle verilir:

${\displaystyle \mu _{n}'={\frac {kx_{\mathrm {m} }^{n}}{k-n}},\,}$

Ancak bu momentler sadece ${\displaystyle k>n}$ icin anlamlıdır.

• Bu demektir ki, katsayıları ${\displaystyle x}$ ile ${\displaystyle \mu _{n}'/n!}$ olan bir Taylor serisi şeklinde tanımlanan moment üreten fonksiyon tanımlanmamıştır.
• Karakteristik fonksiyonu şöyle verilir:

${\displaystyle \varphi (t;k,x_{\mathrm {m} })=k(-ix_{\mathrm {m} }t)^{k}\Gamma (-k,-ix_{\mathrm {m} }t),}$

Burada Γ(a,x) bir tamamalanmamış Gamma fonksiyonu olur.

• Pareto dağılımının bir üstel dağılım ile şu şekilde ilişkisi bulunur:

${\displaystyle f(x;k,x_{\mathrm {m} })=\mathrm {Ustel} (\ln(x/x_{\mathrm {m} });k).\,}$

• Dirac delta fonksiyonu Pareto dağılımının bir limit halidir.

${\displaystyle \lim _{k\rightarrow \infty }f(x;k,x_{\mathrm {m} })=\delta (x-x_{\mathrm {m} }).\,}$

Bir karakterizasyon teoremi

Bağımsız ve hepsi aynı dağılımlı rassal değiskenler olan X_i, i = 1, 2, 3, ... in k > 0 değerleri için [k, ∞) aralığında desteklenen olasılık dağılımları bulunduğu kabul edilsin. Ayrıca, tüm n değerleri için şu iki rassal değişken olan

min{ X₁, ..., X_n } ve :(X₁ + ... + X_n)/min{ X₁, ..., X_n }

birbirinden bağımsız değişkenler oldukları varsayılsın.

Bu halde her iki değişken de Pareto dağılım gösterir.

Zipf'in yasası ile ilişki

Pareto dağılımı sürekli olasılık dağılımdır. Zipf'in yasası veya diğer adı ile zeta dağılımı sürekli Pareto dağılımının araklıklı dağılım karşılığıdır.

Pareto, Lorenz ve Gini

Birkaç Pareto dağılımı için Lorenz eğrileri. k = ∞ kusursuzca eşit dağılımı gösterir (G = 0) ve k = 1 doğrusu ise tüm olarak eşitsiz dağılım gösterimidir (G = 1)

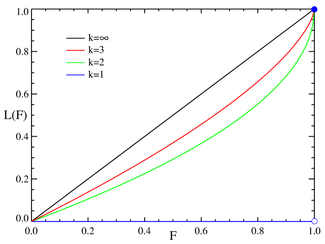
Lorenz eğrisi gösterimi çok kere servet veya gelir dağılımını karakterize etmek için kullanılır.^[1] Herhangi bir gelir veya servet dağılımı için Lorenz eğrisi L(F) olarak ifade edilip ya bir olasılık yoğunluk fonksiyonu olan ${\displaystyle (f(x))}$ veya yığımlı dağılım fonksiyonu olan ${\displaystyle (F(x))}$ ile şöyle ifade edilebilir:

${\displaystyle L(F)={\frac {\int _{x_{\mathrm {m} }}^{x(F)}xf(x)\,dx}{\int _{x_{\mathrm {m} }}^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}}$

Burada x(F) yığımlı dağılım fonksiyonunun tersidir.

Şu Pareto dağılımı için

${\displaystyle x(F)={\frac {x_{\mathrm {m} }}{(1-F)^{1/k}}}}$

Lorenz eğrisi şöyle hesaplanabilir:

${\displaystyle L(F)=1-(1-F)^{1-1/k},\,}$

L(F) ifadesinin paydası x in ortalama değeri olduğu icin, k değeri 1'e eşit veya 1den büyük olmalıdır. Birkaç Pareto dağılımı ile ilişkili Lorenz eğrileri yukarıdaki gösterimde görülebilir.

Gini katsayısı Lorenz eğrisi ile dağılımda-eşitlik ifade eden [0,0] ile [1,1] noktalarını bağlayan çapraz doğru arasındaki farkı, yani eşitlikten sapmayı, ölçen bir katsayıdır. Özellikle gösterilmiştir ki, Gini katsaysı, Lorenz eğrisi ile dağılımda-eşitlik doğrusu arasındaki alanın yuzolçümünün iki mislidir.^[2].

Bu halde Pareto dağılımı icin Gini katsayısı şöyle hesaplanır:

${\displaystyle G=1-2\int _{0}^{1}L(F)\,dF={\frac {1}{2k-1}}}$

Parametre kestirimi

Verilmis bir rastgele orneklem veri dizisi olan ${\displaystyle x=(x_{1},x_{2},\dots ,x_{n})}$ icin k ve ${\displaystyle x_{\mathrm {m} }}$ parametreli Paretoi dagilimi icin olabilirlilik fonksiyonu soyle verilir:

${\displaystyle L(k,x_{\mathrm {m} })=\prod _{i=1}^{n}{k{\frac {x_{\mathrm {m} }^{k}}{x_{i}^{k+1}}}}=k^{n}x_{\mathrm {m} }^{nk}\prod _{i=1}^{n}{\frac {1}{x_{i}^{k+1}}}.\!}$

Boylece logaritmik olabilirlilik fonskiyonu su olur:

${\displaystyle \ell (k,x_{\mathrm {m} })=n\ln k+nk\ln x_{\mathrm {m} }-(k+1)\sum _{i=1}^{n}{\ln x_{i}}.\!}$

Bu fonksiyondan gorulmektedir ki ${\displaystyle \ell (k,x_{\mathrm {m} })}$ terimi ${\displaystyle x_{\mathrm {m} }}$ ile monotonik artis gostermektedir. Yani ${\displaystyle x_{\mathrm {m} }}$ değeri ne kadar buyuk olursa olabilirlilik fonksiyonun değeri de oylece buyuk olacaktir. ${\displaystyle x\geq x_{\mathrm {m} }}$ oldugu icin sonuc olarak

${\displaystyle {\widehat {x}}_{\mathrm {m} }=\min _{i}{x_{i}}.}$

cikartilmaktadir.

k icin bir kestrimci bulmak icin, bunun gerekli kismi turevini almak; yani

${\displaystyle {\frac {\partial \ell }{\partial k}}={\frac {n}{k}}+n\ln x_{\mathrm {m} }-\sum _{i=1}^{n}{\ln x_{i}}=0.}$

ve bunun nerede ifira esit oldugunu bulmak gereklidir. Boylece, k icin maksimum olabilirlilik kestirimi su olur:

${\displaystyle {\widehat {k}}={\frac {n}{\sum _{i}{\left(\ln x_{i}-\ln {\widehat {x}}_{\mathrm {m} }\right)}}}.}$

Bunun beklenen istatistiksel hatasi soyle ifade edilir:

${\displaystyle \sigma ={\frac {\widehat {k}}{\sqrt {n}}}.}$ ^[3]

Grafik olarak gösterim

Pareto dağılımı için dogrusal ölçek kullanılarak elde edilen gösterimdeki eğrinin genel olarak ortaya çıkartığı uzun kuyruk özelliği, ayni veri dizisi logaritma-logaritma ölçekli bir grafikte gösterilince ortadan kalkmakta ve negatif eğim gösteren bir doğru ortaya çıkmaktadır.

Pareto dağılımı simulasyonu

Pareto olasilik dagilimi simulasyonu icin bircok komputer istatistik paketinden yardim gorme imkâni su anda bulunmamaktadir. Oysaki Pareto dagilimi ozellikle aktureya hesaplari icin, ozellikle portfoy maliyetlerinin hesaplamasi icin, cok sik olarak kullanilmasi gerekmektedir ve bu hesaplar icin istatistik paketleri ozel Pareto dagilimi simulasyonlari vermemektedirler.

Diger taraftan istatistik paketlerinin verdikleri bazi ozel olasilik dagilimi simulasyonlarini birbirine ekliyerek Pareto dagilimi gosteren rassal degisken simulasyon sonuclari cikartmak zor degildir. Bu surec kolayca basarilmasi icik yordam soyle verilebilir:

Birinci sekilde bir gamma dagilimi tarafinda uretilen bir rastgele orneklem icin bulunan λ ile bir ustel dagilimdan rastgele sayilar ortaya cikartilir; yani

${\displaystyle \displaystyle k_{\mathrm {Gamma} }=k_{\mathrm {Pareto} }\,}$

ve

${\displaystyle \theta _{\mathrm {Gamma} }={\frac {1}{x_{\mathrm {m} _{\mathrm {Pareto} }}}}.}$

Bu hesaplar 0da baslayan bir rastgele veri serisi uretirler. Bunun ustune ${\displaystyle x_{\mathrm {m} }}$ eklemek gerekir.

Diger bir sekilde simulasyon, ters donusum orneklem alma islemi kullanılarak elde edilir. ${\displaystyle (0;1)}$ birim araklita bulunan surekli tekduze dagilimdan ${\displaystyle U}$ degisebiliri icin rastgele olarak elde edilir. Bu degisebilir icin

${\displaystyle T={\frac {x_{\mathrm {m} }}{U^{1/k}}}}$

fonksiyonu Pareto-dagilimi gosterir.^[4]

Ayrıca bakınız

• Pareto prensipi
• Pareto enterpolasyonu
• Pareto etkinliği
• Pareto analizi
• The Long Tail

Kaynakça

1. Lorenz,M.O. (1905). "Methods of measuring the concentration of wealth." Publications of the American Statistical Association. C.9 say.209–219.
2. Aabergé,R. (2005) kaynak International Conference to Honor Two Eminent Social Scientists, Mayıs 2005 toplantısında bildiri -- http://www.unisi.it/eventi/GiniLorenz05/25%20may%20paper/PAPER_Aaberge.pdf
3. http://aps.arxiv.org/PS_cache/cond-mat/pdf/0412/0412004v3.pdf
4. http://www.stat.psu.edu/~dhunter/R/2006mle.html

Dış bağlantılar

• Reed,W.J. Pareto, Zipf ve diğer güç yasaları
• SOCR Bilgi Kaynagi: Pareto dagilimina etkilisimli ara yuzey
• Pareto orneklemesi ve simulasyonu