Penrose grafik gösterimi
matematik ve fizik'te, Penrose grafik gösterimi veya tensör diagram gösterimi fonksiyonların veya tensorlerin bir (genellikle el yazısı) görsel tasviri için Roger Penrose tarafından önerilen yöntemdir.[1] Gösterimde bir diyagram gibi çok hatları ile birbirine bağlantılı çeşitli şekiller oluşur tamirci oyuncakları.gösterim Predrag Cvitanović tarafından yaygın olarak incelenmiştir. klasik Lie grupları sınıflandırmak için kullanılır. [2] Ayrıca fizik Dokunmuş ağlar temsil teorisi kullanarak genelleştirilmiş, ve lineer cebir deki matris grup larının iz diyagramı ile varolmuştur .
Yorumlama
Çokludoğrusal cebir
Çokludoğrusal cebir'in dilinde, her şekil bir çokludoğrusal fonksiyon gösterimidir.Bir fonksiyonun girişler veya çıkışları şekillere bağlı hatları temsil eder.ve bir şekilde bir arada ekleme şekilleri fonksiyonların kompozisyonu esastır.
Tensörler
tensor cebiri'nin dilinde,özel olarak tensör yukarı ve aşağı doğru uzanan çok sayıda çizgilerle özel bir şekil ile ilişkilidir,Tensörlerin soyut karşılığı sırasıyla üst ve alt indisleridir.İki şekil arasındaki ara bağlantı indislerin kontraksiyonu'na karşılık gelir . Bir bu gösterim'in bir avantajı yeni indisler için yeni harfler icat etmek zorunda değildir. Bu gösterim is açıkça taban-bağımlıdır.[3]
Matrisler
her şekil bir matrisi gösterir, ve tensör çarpımı yatay olur, ve matris çarpımı dikey olur.
Özel tensörlerin gösterimi
Metrik tensör
metrik tensör bir U-şekli döngüsü tarafından veya bir ters U-şekil döngüsü tarafından gösterimi, kullanılan tensörünün türüne bağlı olarak değişir.
Levi-Civita tensörü
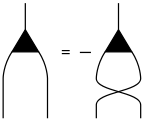
Levi-Civita antisimetrik tensörü tensörün türüne bağlı olarak, aşağı ya da yukarı bakacak kalın yatay çubukları kullanılmaktadır
Yapı sabiti
Bir Lie cebir'inin Yapı sabiti() bir satır yukarıya ve iki satır aşağıyı gösteren küçük bir üçgen tarafından temsil edilir
Tensör operasyonları
İndisin büzülmesi
İndislerin büzülme'si indis çizgileri girişi tarafından gösterilir.
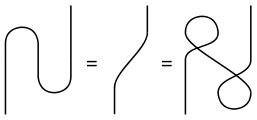 |
Simetrizasyon
İndislerin Simetrizasyon'u bir kalın zig-zag tarafından gösterilir veya yatay indis sıraların çaprazlandığı dalgalı çubuk.
 Simetrizasyon (with ) |
Antisimetrizasyon
İndilerin Antisymmetrizasyon'u yatay indis sıraların çaprazlandığı kalın düz bir çizgi ile temsil.
 Antisimetrizasyon (with ) |
Determinant
Determinant indislere antisimetrizasyon uygulanmasıyla oluşturulur.
 matrisin tersi |
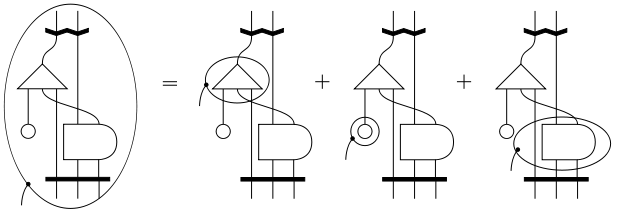
Kovaryant türev
kovaryant türev () bir çemberin çevresindeki the tensör(ler) tarafından farklılaştırılan gösterimdir ve bir çizgi çember türevinin alt indeksini temsil etmek için aşağı doğru işaret giren durumlardır.
 |
Tensör Düzenlemesi
Şematik gösterim tensör cebiri işlenmesi için yararlıdırmanipülasyonlarının birkaç basit kullanılan "özellik" içerir Örneğin , burada n boyutların sayısıdır,bir ortak "özellik"tir.
Riemann eğrilik tensörü
Riemann eğrilik tensörü cinsinden verilen Ricci ve Bianchi kimlikleri gösterimin gücünü göstermektedir
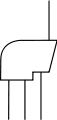 Riemann eğrilik tensörü için gösterim |
 Ricci tensörü |
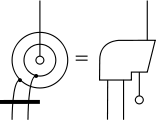 Ricci özdeşliği |
 Bianchi özdeşliği |
Bağlantılar
gösterim spinör'ler ve twistör'ler gösterimini desteklemek için genişletilmiştir.[4][5]
Ayrıca bakınız
- Özet indis gösterim
- Örgülü monoidal kategori
- Kategorik kuantum mekaniği tensör diyagram gösterimi kullanır
- Ricci hesabı
- Spin network lar
- İz diyagramı
- Açısal momentum şemaları (kuantum mekaniği)
Notlar
- ↑ see e.g. Quantum invariants of knots and 3-manifolds" by V. G. Turaev (1994), page 71
- ↑ Predrag Cvitanović (2008). Group Theory: Birdtracks, Lie's, and Exceptional Groups. Princeton University Press. http://birdtracks.eu/.
- ↑ Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, 2005, ISBN 0-09-944068-7, Chapter Manifolds of n dimensions.
- ↑ Penrose, R.; Rindler, W. (1984). Spinors and Space-Time: Vol I, Two-Spinor Calculus and Relativistic Fields. Cambridge University Press. s. 424–434. ISBN 0-521-24527-3. http://books.google.com/books?id=CzhhKkf1xJUC.
- ↑ Penrose, R.; Rindler, W. (1986). Spinors and Space-Time: Vol. II, Spinor and Twistor Methods in Space-Time Geometry. Cambridge University Press. ISBN 0-521-25267-9. http://books.google.com/books?id=f0mgGmtx0GEC.
Şablon:Roger Penrose Şablon:Tensors
