Primoriyel

p_n#'in n'in fonksiyonu olarak logaritmik eğrisi.

n#'in n'nin fonksiyonu diagramının (kırmızı noktalar) n!'le kıyası. Her iki eğri logaritmiktir.

Primoriyel (İngilizce prime (=asal)'dan), matematikte ve bilhassa sayı teorisinde doğal sayılardan doğal sayılara tanımlanmış faktöriyele benzer şekilde ard arda positif tam sayıları çarpacağı yerde sadece asal sayıları çarpar.

Birbiriyle çelişen iki tanımda kullanılan değişkenin mânâsı farklı yorumlanmaktadır: birincisi değişkeni asal sayıların sıralaması olarak yorumlar, dolayısıyla monoton artar. İkinci yorumu değişkeni birbiriyle çarpılacak asal sayılara işaret eder ve dolayısıyla her bileşik sayı için bir önceki değerle aynı değeri alır. Bu maddenin devamında ikinci tanım kullanılacaktır.

Primoriyel adı, bu fonksiyonla faktöriyel arasındaki analojiye işaret eden Harvey Dubner tarafından verilmiştir; faktöryel nasıl faktörlere ilgiliyse primoriyel de asal sayılarla (İng. prime numbers veya kısaca primes) benzer şekilde ilgilidir.

Asal sayılar için tanımı

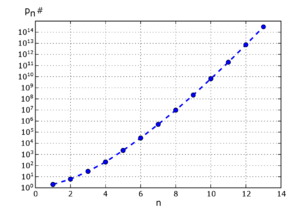
n'inci asal sayı p_n için primoriyel p_n#, ilk n asalın çarpımı olarak tarif edilir:^[1][2]

${\displaystyle p_{n}\#=\prod _{k=1}^{n}p_{k}}$

Burada p_k k'inci asal sayıdır.

Mesela p₅#, ilk beş asalın çarpımını gösterir:

${\displaystyle p_{5}\#=2\times 3\times 5\times 7\times 11=2310.}$

İlk altı primoriyel p_n# are:

1, 2, 6, 30, 210, 2310. (OEIS'de A002110 dizisi)

Diziye p₀# = 1 de boş çarpım olarak eklenmiştir.

Asimtotik olarak primoriyel p_n#,

${\displaystyle p_{n}\#=e^{(1+o(1))n\log n},}$

fonksiyonuna göre artarlar. Burada ${\displaystyle o(\cdot )}$ küçük o gösterimidir.^[2]

Doğal sayılar için tanımı

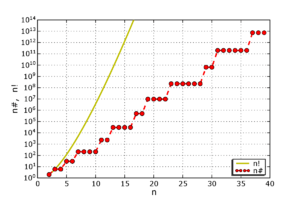
Genelde n pozitif tam sayısı için n# ≤ n olan bütün asalların çarpımı olarak da tarif edilebilir:^[1][3]

${\displaystyle n\#=\prod _{i=1}^{\pi (n)}p_{i}=p_{\pi (n)}\#}$

Burada ${\displaystyle \scriptstyle \pi (n)}$ asal sayan fonksiyon (OEIS'de A000720 dizisi) olup ≤ n olan asal sayıların kaç tane olduğunu haber verir.

Bu tanım, aynı zamanda şuna da eşittir.

${\displaystyle n\#={\begin{cases}1&{\text{if }}n=1\\n\times ((n-1)\#)&{\text{if }}n>1\ \And \ n{\text{ is prime}}\\(n-1)\#&{\text{if }}n>1\ \And \ n{\text{ is composite}}.\end{cases}}}$

Mesela 12#, 12'den küçük asal sayıların çarpımıdır:

${\displaystyle 12\#=2\times 3\times 5\times 7\times 11=2310.}$

${\displaystyle \scriptstyle \pi (12)=5}$ olduğundan bu değer

${\displaystyle 12\#=p_{\pi (12)}\#=p_{5}\#=2310}$

şeklinde hesaplanır.

Bu tanıma göre ilk 12 primoriyel n# şöyledir:

1, 2, 6, 6, 30, 30, 210, 210, 210, 210, 2310, 2310.

Görüldüğü gibi bileşik n için her terim n#, tarifinde de görüldüğü gibi bir önceki terimin eşidir (n − 1)#. Yukarıdaki örnekte 12 bileşik sayı olduğundan 12# = p₅# = 11#'dir.

n#'nin tabii logaritması birinci Çebişev fonksiyonu olup ${\displaystyle \theta (n)}$ veya ${\displaystyle \vartheta (n)}$ şeklinde yazılır. Bu fonksiyon büyük n 'ler için lineer n 'ye yaklaşır.^[4]

n# primoriyeli

${\displaystyle \ln(n\#)\sim n.}$

fonksiyonuna göre büyür.

Bütün bilinen asal sayıları çarpma fikri asal sayıların sonsuzluğu ile ilgili bâzı ispatlarda geçmekte olup başka bir asal sayının varlığını türetmek için kullanılır.

Özellikler ve uygulamalar

Primoriyeller, aritmetik artışlarda asal sayıları aramada bir rol oynar. Mesela 2236133941 + 23# bir asal sayıdır ve onüç asal sayıdan oluşan bir dizinin başıdır. Bu dizi, yukarıdaki asal sayıya 23# eklemekle elde edilir, onüçüncü ve sonuncu elemanı da 5136341251'dir. 23#, aynı zamanda onbeş ve onaltı asalın aritmetik progresyonunda ortak farkı teşkil eder.

Her yüksek derecede bileşik sayı primoriyellerin çarpımıdır (mesela 360 = 2·6·30).^[5]

Primoriyeller karesiz tam sayılar olup kendisilerinden küçük herhangi bir sayıdan daha fazla farklı asal faktörleri vardır. Her primoriyel n için ${\displaystyle \phi (n)/n}$ kesri, kendisinden küçük her tam sayı için olan kesirden küçüktür. Burada ${\displaystyle \phi }$ Euler'in totient fonksiyonudur.

Görünüm

Birden büyük pozitif tam sayılar için Riemann zeta fonksiyonu^[6], primorieller ve ${\displaystyle J_{k}(n)}$ Jordan'ın totient fonksiyonunu kullanarak hesaplanabilir:

${\displaystyle \zeta (k)={\frac {2^{k}}{2^{k}-1}}+\sum _{r=2}^{\infty }{\frac {(p_{r-1}\#)^{k}}{J_{k}(p_{r}\#)}},\quad k=2,3,\dots }$

Primoriyellerin tablosu

n	n#	pn	pn#
0	1	asal yok	1
1	1	2	2
2	2	3	6
3	6	5	30
4	6	7	210
5	30	11	2310
6	30	13	30030
7	210	17	510510
8	210	19	9699690
9	210	23	223092870
10	210	29	6469693230
11	2310	31	200560490130
12	2310	37	7420738134810
13	30030	41	304250263527210
14	30030	43	13082761331670030
15	30030	47	614889782588491410
16	30030	53	32589158477190044730
17	510510	59	1922760350154212639070
18	510510	61	117288381359406970983270
19	9699690	67	7858321551080267055879090
20	9699690	71	557940830126698960967415390

Kaynaklar

1. Eric W. Weisstein, Primorial (MathWorld), Eric W. Weisstein. "Primorial". 30 Nisan 2016 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20160430165620/http://mathworld.wolfram.com/Primorial.html. Erişim tarihi: 2015-05-06. 
2. (OEIS'de A002110 dizisi)
3. (OEIS'de A034386 dizisi)
4. Eric W. Weisstein, Chebyshev Functions (MathWorld)
5. "Sloane's A002182 : Highly composite numbers", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
6. Mező, István (2013). "The Primorial and the Riemann zeta function". The American Mathematical Monthly 120 (4): 321. 

• Harvey Dubner, "Factorial and primorial primes". J. Recr. Math., 19, 197–203, 1987.

Ayrıca bakınız

• Bonse eşitsizliği
• Faktöriyel sayı sistemi
• Primoriyel asal sayı