Schild'in merdiveni

the book için Schild'in merdiveni sayfasına bakınız.

of Schild'in merdiveninin iki basamağı.A₁X₁ ve A₂X₂ parçaları A₀X₀'ın eğrisi boyunca paralel taşınımının ilk sırasıyla bir yaklaşıklıktır.

Genel görelilik teorisinde, ve daha geneli diferansiyel geometri de, Schild'in merdiveni için bir eğri boyunca bir vektörün paralel taşınım yaklaşıklığı için yalnızca bir ilk-sıra metot olan afinleştirilmiş ölçeklendirme geodezikleri kullanılıyor.Alfred Schild kendi adına olan bu metodu Princeton Üniversitesinde ders sırasında tanıttı.

Yapım

Birim uzunluk ${\displaystyle A_{0}X_{0}}$ ın bir jeodezik segmenti ile bir ${\displaystyle A_{0}}$ noktasında bir tanjant vektörü x tanımlamak ve Levi-Civita paralelkenarımsının bir yaklaşığı olarak yaklaşık paralel taraf ${\displaystyle A_{0}X_{0}}$ ve ${\displaystyle A_{1}X_{1}}$ ile yaklaşık bir paralelkenar oluşturmak için bir fikirdir; Yeni parça ${\displaystyle A_{1}X_{1}}$ böylece ${\displaystyle A_{1}.}$ de bir yaklaşık paralel öteleme tanjant vektörüne karşılık gelir

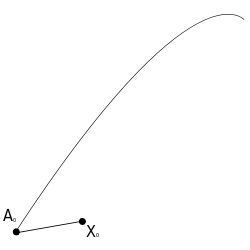A curve in M with a "vector" X0 at A0, Bir jeodezik bölüm olarak burada tanımlanan.

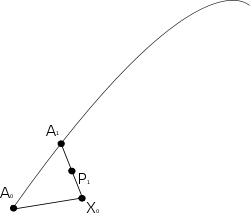Select A1 on the original curve. The point P1 is the midpoint of the geodesic segment X0A1.

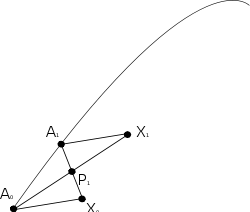The point X1 is obtained by following the geodesic A0P1 for twice its parameter length.

Resmi olarak, bir γ eğrisi düşünelim bir Riemann manifoldu M içinde bir A₀ noktası yardımıyla, ve diyelimki x A₀'da bir tanjant vektör olsun. x ise bir jeodezik parça ile ayrıştırılabilir A₀X₀ yoluyla üstel göndermedir. Bu jeodezik σ yeterlidir

${\displaystyle \sigma (0)=A_{0}\,}$

${\displaystyle \sigma '(0)=x.\,}$

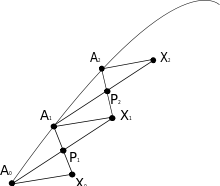
Schild'in merdiveni yapımı adımlardır:

• Diyelimki X₀ = σ(1), böylece jeodezik parça ${\displaystyle A_{0}X_{0}}$ birim uzunluk var.
• şimdi diyelimki A₁ γüzerinde bir nokta olsun A₀ ya yakın, ve jeodezik yapı X₀A₁.
• Diyelimki bu hassaslık içinde X₀A₁'ın orta noktası P₁ olsun X₀P₁ parçaları ve P₁A₁ bir afin geçiş için parametre eşit alınır.
• A₀P₁ jeodezik yapımı, ve bu bir nokta X₁'a uzanır böylece A₀X₁'in parametre uzunluğu A₀P₁'in bu çiftidir.
• Sonuçta A₁X₁ jeodezik yapımıdır.Bu jeodezik x₁'e tanjant paralel taşınım ise X₀'ın A₁'ya, en azından ilk sırasına.

Yaklaşıklık

Bu paralel taşınımın devamlı sürecinin ayrık bir yaklaşıklığıdır. Eğer ortam uzayı düzse, bu tam paralel taşınım, ve paralelkenar tanım adımları Levi-Civita paralelkenarımsı ile uyumludur.

Bir eğri uzay içinde, hata holonomi ile veriliyor ${\displaystyle A_{1}A_{0}X_{0},}$ üçgeni çevresinde bu üçgenin içi üzerinde eğrinin integraline eşittir,Ambrose-Singer teoremi ile; bu Green teoreminin bir formudur (iç üzerinde integrale ilişkin bir eğri çevresindeki integral).

Notlar

1. Schild'in merdiveni jeodezikler ama aynı zamanda jeodezikler birlikte göreceli mesafe sadece gerektirmez. Bağıl mesafe gerekli orta noktaları tespit edilebilir olan jeodezikler arasında afin parametreleriyle ile sağlanabilir.
2. Schild'in merdiveni paralel taşıma ille torsiyon-serbest inşa edilmiştir
3. Bir Riemannian metrik jeodezikler oluşturmak için gerekli değildir.Geodezikler bir Riemann metrik oluşturulur eğer bu bağlantı torsiyon serbest olarak tanımlanır çünkü Ama, Schild'in merdiveni ile sınıra inşa edilmiştir paralel taşıma Levi-Civita bağlantısı olarak aynıdır.

Kaynakça

• Kheyfets, Arkady; Miller, Warner A.; Newton, Gregory A., Schild's ladder parallel transport procedure for an arbitrary connection. International Journal of Theoretical Physics

20001200, Volume 39, Issue 12, pp 2891-2898 .

• Misner, Charles W.; Thorne, Kip S.; Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0