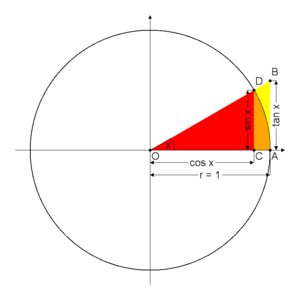Sinüs teoremi

Sinüs teoremi

Sinüs teoremi, bir çembersel üçgende (kirişler üçgeni) bir kenar ve bu kenar karşısındaki açının sinüsleri oranı sabittir. Sinüs, dik açılı üçgenlerde dik olmayan bir açının karşısında kalan dik kenar ile hipotenüs (dik açının karşısında kalan kenar) ün birbirine oranıdır.

a, b, ve c üçgenin kenar uzunlukları, A, B ve C üçgenin iç açıları ve r çevrel çemberin yarı çapı ise bunlar arasında sinüs teoremine göre aşağıdaki bağıntı mevcuttur:

${\displaystyle {a \over \sin A}={b \over \sin B}={c \over \sin C}=2r\,}$

İspatı

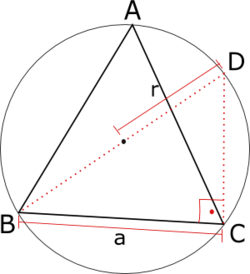
Sinüs Teoremi ispatında kullanılan şekil

1. ABC üçgeninin çevrel çemberinin merkezi O ve yarıçapı r olsun. BO ve OC yarıçapları çizildiğinde aynı yayı gören çevre ve merkez açılardan dolayı ${\displaystyle m(BOC)=2m(A)}$ olur.
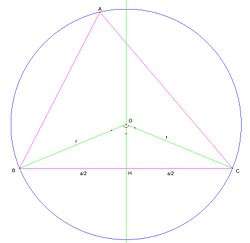
2. O merkezinden a kenarına H noktasında yükseklik inildiğinde BOC ikizkenar üçgen olduğundan yükseklik hem kenarortay hem de açıortay olur. O zaman BOH üçgeni bir açısı ${\displaystyle m(BOH)=A}$ derece olan dik üçgen olur. |BH| uzunluğu ise a/2 dir.
3. Sinüsün tanımı gereği,

${\displaystyle \sin BOH=\sin A={\frac {a/2}{r}}}$ Bu işlem düzenlendiğinde

${\displaystyle {a \over \sin A}=2r}$ bulunur.

Aynı işlem diğer kenarlar için de yapıldığında sinüs teoremi bulunmuş olur.