Öklid geometrisi
| Geometri |
|---|

{{{altyazu}}} |
| Geometrinin tarihi |
|
Dalları
Öklidci geometri · Öklid dışı geometri · Analitik geometri · Riemannian geometrisi · Diferansiyel geometri · Tasarı geometri · Cebirsel geometri
|
|
Araştırma alanları
|
|
Önemli kavramlar
Nokta · Doğru · Dik · Paralel · Doğru parçası · Düzlem · Uzunluk · Alan · Hacim · Köşe · Açı · Eşlik · Benzerlik · Çokgen · Üçgen · Yükseklik · Hipotenüs · Pisagor teoremi · Dörtgen · Yamuk · Uçurtma · Paralelkenar (Dikdörtgen, Eşkenar dörtgen, Kare) · Köşegen · Simetri · Eğri · Daire · Çap · Silindir · Küre · Piramit · Boyutlar (Bir, İki, Üç, Dört)
|
|
Geometriciler
Aryabhata · Ahmes · Apolonius · Archimedes · Baudhayana · Bolyai · Brahmagupta · Euclid · Pisagor · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · Kātyāyana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kōhan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng
|
Öklidci geometri, İskenderiye'li matematikçi Öklid tarafından ortaya atılan bir geometri sınıfıdır.
Öklid'in beş aksiyomu şunlardır:
- İki noktadan bir ve yalnız bir doğru geçer.
- Bir doğru parçası iki yöne de sınırsız bir şekilde uzatılabilir.
- Merkezi ve üzerinde bir noktası verilen bir çember çizilebilir.
- Bütün dik açılar eşittir.
- Bir doğruya dışında alınan bir noktadan bir ve yalnız bir paralel çizilebilir.
Bağıntılar
Yükseklik bağıntısı
Bir dik üçgende hipotenüse ait yükseklik uzunluğunun karesi, hipotenüs üzerinde ayırdığı 2 kenarın çarpımına eşittir.
Dik kenar bağıntısı
Bir dik üçgende bir dik kenarın uzunluğunun karesi, bu kenarın hipotenüs üzerindeki dik izdüşümü ile hipotenüs uzunluğunun, çarpımına eşittir. Bu bağıntıya Öklid’in Dik Kenar Bağıntısı denir.
Öklid bağıntısı
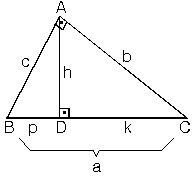
Öklid bağıntısı
- (alan formülünden)
This article is issued from Vikipedi - version of the 11/9/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.