Eşlik

Eşlik, iki veya daha fazla geometrik cismin özellikleri bakımından birebir aynı olmasıdır. Eş olan cisimlerin yönlerinin veya bulundukları noktanın değişmesi eşliği bozmaz. Eşliğin sembolü ${\displaystyle \cong }$'dir.

Bir Boyutlu Cisimlerde

Bir boyutlu cisimlerde tek ölçü vardır: uzunluk. Yani iki doğru parçasının aynı uzunlukta olması yeter. Hangi yöne dönük olursa olsun.

Not:Bütün noktalar eştir.

Eş altıgenler

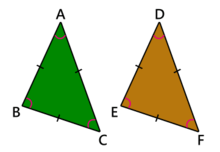
İki Boyutlu cisimlerde

İki boyutlu cisimlerin en ve boy olmak üzere iki ölçüleri vardır. Yani bir dikdörtgeni ele alırsak bu dikdörtgenin iki farklı uzunluğunun aynı olması ona eş dememize yetecektir.

İki adet eş üçgen Görüldüğü üzere bütün kenarları aynı

Üç Boyutlu Cisimlerde

Üç boyutlu cisimlerde durum biraz daha değişir çünkü en ve boyun yanına yükseklik denilen kavram da eklenmiştir ki diğer tüm cisimlerde olduğu gibi üç boyutlu cisimlerde de bu ölçüler aynı yerdeyse ( yani aynı ölçüler aynı doğru parçasındaysa ) cisimler eştir.