İstatistik
İstatistik veya sayıtım, belirli bir amaç için veri toplama, tablo ve grafiklerle özetleme, sonuçları yorumlama, sonuçların güven derecelerini açıklama, örneklerden elde edilen sonuçları kitle için genelleme, özellikler arasındaki ilişkiyi araştırma, çeşitli konularda geleceğe ilişkin tahmin yapma, deney düzenleme ve gözlem ilkelerini kapsayan bir bilimdir. Belirli bir amaç için verilerin toplanması, sınıflandırılması, çözümlenmesi ve sonuçlarının yorumlanması esasına dayanır.
Fizik doğa bilimler ve sosyal bilimlere kadar geniş bir alanda uygulanabilmektedir. Aynı zamanda iş dünyası ve hükûmetle ilişkili tüm alanlarda karar almak amacıyla kullanılır. İstatistik yukarıdaki anlamıyla tekildir. Sözcüğün çoğul anlamı, "sistemli bir şekilde toplanan sayısal bilgiler"dir. Örnek olarak nüfus istatistikleri, çevre istatistikleri, spor istatistikleri, milli eğitim istatistikleri verilebilir.
İstatistiği öğrenmedeki amaç, bir araştırmada elde edilen verilerin uygun istatiksel yöntemler kullanılarak yorumlanacağını bilmektir.
İstatistiksel yöntemler, toplanmış verilerin özetlenmesi veya açıklanması amacıyla kullanılır. Bu tür bir yaklaşım betimsel istatistik adını alır. Buna ek olarak verilerdeki örtüşmelerin (kalıplar veya örüntüler), gözlemlerdeki rassallığı ve belirsizliği göze alacak şekilde, üzerinde çalışılan anakütle veya süreç hakkında sonuç çıkarma amacıyla modellenmesi, çıkarımsal istatistik adını alır. Hem betimsel istatistik hem de tahminsel istatistik, uygulamalı istatistiğin parçaları olarak sayılabilir. Matematiksel istatistik adı verilen disiplin ise konunun teorik matematiksel altyapısını inceleyen disiplindir.
İstatistiğin diğer bölümlerle olan ilişkilerinden doğan kavramlar şu şekilde gösterilebilir: Ekonomi+İstatistik = Ekonometri, Psikoloji+İstatistik = Psikometri , Tıp+İstatistik = Biyoistatistik , Sosyoloji+İstatistik = Sosyometri, Tarih+İstatistik=Kliometri.
İstatistik kelimesi Modern Latincedeki statisticum collegium (devlet konseyi) ve İtalyancadaki statista (devlet adamı, politikacı) kelimelerinden türemiştir. Kelime ilk olarak Almanca'da Gottfried Achenwall tarafından devlete ait verilerin sunulduğu Statistik (1749) adlı eserde devlet bilimi anlamında kullanılmıştır. Bu tanımı içeren İngilizce terim ise o dönemde political arithmetic (siyasi aritmetik) olarak geçmekteydi. İstatistik kelimesi veri toplama ve sınıflandırma anlamını ise yaklaşık olarak 19. yüzyılın başlarında kazandı. Terim İngilizce'ye Sir John Sinclair tarafından aktarıldı. Statistik adlı eserin temel amacı hükümet tarafından ve yönetimsel organlar tarafından kullanılacak veriler sunmaktı. Eyaletler, ve yerel bölgeler hakkında bilgi toplama işi ulusal ve uluslararası istatistik kurumları tarafından sürdürülmektedir. Daha dar anlamda nüfus hakkında düzenli bilgiler ise nüfus sayımları ile elde edilir.20. yüzyıl boyunca kamu sağlığı ile ilgili konularda (epidemiyoloji, biyoistatistik), ekonomik ve sosyal (işsizlik, ekonometri gibi) alanlarda daha titiz araçlara ihtiyaç duyulması istatistiksel uygulamalarda ilerlemeyi zorunlu kılmıştır. Bu ihtiyaç özellikle I. Dünya Savaşı sonucu gelişen, nüfusları hakkında derin bilgi sahibi olmak isteyen refah devletlerinde daha belirgin olmuştur. Bu anlamda "toplum yönetimi adına bilgi toplama isteği" filozof Michel Foucault tarafından biyogüç olarak nitelendirilmiştir, bu terim daha sonra pek çok yazar tarafından da kullanılmıştır. İstatistiğin matematiksel temelleri Pierre Fermat ve Blaise Pascal'ın 1654 yılına kadar giden olasılık kuramı hakkındaki yazışmalarına dayanır. Christiaan Huygens (1657) konunun bilinen ilk bilimsel uygulamasını sunmuştur. Jakob Bernoulli'nin Ars Conjectandi (posthumous, 1713) ve Abraham de Moivre'nin Doctrine of Chances (1718) adlı eserleri konuya matematiğin bir dalı olarak yaklaşmıştır.
Hata teorisi Roger Cotes'nin Opera Miscellanea (posthumous, 1722) adlı eserine dayanır , fakat teorinin gözlem hatalarına uygulanmasının ilk örneği Thomas Simpson tarafından 1755'te yazılan (basım: 1756) bir bildiride bulunur. Bu bildirinin 1757 yılındaki tekrar basımı pozitif ve negatif hataların eşit derecede olasılıklı olduğu aksiyomunu kabul ederken, bütün hataları içinde bulunduracağını varsayabileceğimiz belirli tanımlanabilir limitlerin varlığından söz ederek "sürekli hatalar"ı ve bir olasılık eğrisini sunar.
Pierre-Simon Laplace , olasılık teorisinin ilkelerine dayanarak gözlem kombinasyonları için bir kural geliştirmeye çalıştı (1774). Hata olasılıkları kanununu bir eğri ile gösterdi.
Kavramsal Bakış
İstatistiğin bilimsel, endüstriyel veya toplumsal bir probleme uygulanmasında önce üzerinde çalışılan süreç veya anakütle ele alınır. Bu anakütle bir ülkedeki insanların nüfusu, kayadaki kristal miktarı veya belirli bir fabrikanın belirli bir dönemde ürettiği mallar olabilir. Bunun yerine farklı zamanlarda gözlenen bir süreç de olabilir; bu şekilde toplanan veri zaman serisi adını alır.
Pratik nedenlerden ötürü, bütün bir anakütle hakkında veri toplamak yerine genelde anakütleden seçilen bir altküme (örnek veya örneklem) üzerinde çalışılır. Örnek hakkındaki veri deney veya gözlem yoluyla elde edilir. Bundan sonra veri istatistiksel analize tâbi tutulur. Bunun iki amacı vardır: açıklama (betimleme) ve sonuç çıkartma.
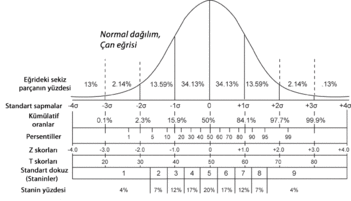
- Betimsel istatistik, örneklemi sayısal veya grafiksel olarak özetlemek amacıyla kullanılabilir. Sayısal göstergelere temel örnek olarak ortalama ve standart sapma gösterilebilir. Grafiksel özetler çeşitli türde grafik ve tabloları içerir.
- Çıkarımsal istatistik verideki örtüşmeleri modellemek için kullanılır, olasılığı göze alır ve daha büyük bir istatistiksel yığın hakkında sonuç çıkarır. Bu sonuçlar, evet/hayır şeklinde cevaplar olabileceği gibi (hipotez testi), sayısal özelliklerin tahmin edilmesi (istatistiksel tahmin) gelecekteki değerlerin öngörülmesi (istatistiksel öngörü), veriler arasındaki doğrusal ilişkinin yorumlanması (korelasyon), veya bu ilişkilerin modellenmesi (regresyon analizi) şeklinde olur. Diğer belli başlı matematiksel modelleme teknikleri varyanslar analizi ANOVA, zaman serisi, ve veri madenciliğidir.
Burada özellikle korelasyon konusu ele almaya değerdir. Bir veri kümesinin analizi iki değişkenin beraber hareket ettiğini (yani ele alınan ana kütlenin iki özelliğinin benzerlik gösterdiğini) ortaya çıkarabilir. Örneğin yıllık gelirle yaşam süresini ele alan bir çalışma fakir insanların varlıklı insanlardan daha kısa bir yaşam süresine sahip olduğunu bulabilir. Burada gelirle yaşam süresi arasında bir korelasyon olduğu söylenebilir. Fakat buradan asla gelir yaşam süresinin sebebidir veya sonucudur anlamı çıkarılmamalıdır.
Eğer örneklem, anakütleyi temsil etme yeterliliğine sahipse, örnekten elde edilen sonuçlar ve çıkarımlar bir bütün olarak anakütle hakkında bilgi verebilir. Burada asıl problem seçilen örneklemin anakütleyi temsil kabiliyetine sahip olup olmamasıdır. İstatistik, örneklemde ve veri toplama sürecinde ortaya çıkan hataları gideren, örneklemin rassal olmasını sağlayan araçlar sunar. Aynı zamanda güvenilir deneysel sonuçların elde edilmesini sağlayan yöntemler de sunar.
Bu şekilde bir rassallığın anlaşılmasını sağlayan temel matematiksel kavram olasılıktır. Matematiksel İstatistik (İstatistik kuramı), İstatistiğin Matematiksel altyapısını incelemek için Olasılık kuramı ve Matematiksel Analizden faydalanan Uygulamalı Matematik dalıdır.
İstatistiksel yöntemler
Deneye ve gözleme dayalı çalışmalar
İstatistiksel araştırmaların ortak amaçlarından biri nedenselliği incelemek ve özelde tahmin edicilerdeki veya bağımsız değişkenlerdeki bir değişimin bağımlı değişken üzerindeki etkisini incelemektir. Nedenselliği ele alan temelde iki tür istatistiksel yöntem bulunur: deneysel çalışmalar ve gözleme dayalı çalışmalar. İki çalışma türünde de bağımsız değişken veya değişkenlerdeki farklılıkların gözlenen bağımlı değişken üzerindeki etkisi incelenir. Bu çalışma türlerinde oluşan fark ise yöntemin uygulanma biçimidir. Yöntemlerin ikisi de verimli sonuçlar ortaya koyabilir.
Deneysel yöntemde çalışılan sistem üzerinde bir takım ölçümler yapılır, sistem üzerinde oynamalar yapılır, ve bu oynamaların sistem üzerinde etkisi olup olmadığını anlamak için tekrar ölçüm yapılır. Gözleme dayalı yöntemde ise sisteme müdahale olmaz, bunun yerine veri toplanır ve tahmin edicilerle (bağımsız değişkenler) tepki değişkenleri(bağımlı değişkenler) arasındaki örüntüler araştırılır.
Deneysel çalışmaya örnek olarak Western Elektrik Şirketi'nde aydınlatmanın çalışanlar üzerindeki etkisini araştıran Hawthorne deneyi verilebilir. Deneyde önce santraldeki üretim ölçülmüş, daha sonra kayan bant etrafında çalışan işçilerin aydınlatma koşulları değiştirilmiştir. Bütün deney sonuçları aydınlatmanın verimliliği arttırdığını göstermiştir. Ne var ki bu çalışmanın sonuçları deneysel yöntemdeki hatalar sebebiyle ciddi eleştiriler almıştır. Örneğin çalışmada kontrol grubu kullanılmamıştır.
Gözleme dayalı çalışmaya örnek olarak sigara kullanımı ve akciğer kanseri arasındaki bağınıtıyı inceleyen bir araştırma gösterilebilir. Bu tür çalışmada ilgi alanları hakkında bilgi toplamak için anket yöntemini kullanır ve sonra bilgiler istatistiksel analiz altında incelenir. Bu örnekte araştırmacılar sigara içen ve sigara içmeyen gruplardan bilgi toplar ve her iki gruptaki kanser vakası sayısı ele alınarak karşılaştırılır.
Bir deneyin temel adımları:
1. Araştırmanın planlanması, bilgi kaynaklarının, araştırmanın konusunun belirlenmesi, öne sürülen yöntemdeki ahlaki yönlerin ele alınması.
2. Sistemin modellenmesi, bağımlı ve bağımsız değişkenler arasındaki ilişkiye odaklanma.
3. Bir gözlem grubunu ortak yönlerini ele alacak şekilde özetlemek.
4. Gözlemlediğimiz dünya hakkında sayıların bize neler söylediğini açıklamak.
5. Çalışmanın sonuçlarını belgelemek ve sunmak.
Ölçülme ölçekleri
İstatistik verileri sayılar halinde olup bu sayılar için dört çeşit ölçülme ölçeği şeklinde elde edilme olabilirliği vardır. Bu verilerin dört çeşit ölçülme ölçeği olabileceğini ilk defa 1946da Amerikan istatistikçi Stanley Stevens ortaya atmıştır. Stevens'in dört ölçülme ölçeği şunlardır: isimsel, sırasal, aralıksal ve oransal. Her bir değişik ölçülme ölçeğine göre elde edilen istatistiksel veriler değişik matematiksel güçte olup her biri için kullanılabilecek matematik işlemler ve betimleyici ve çıkarımsal istatistiksel işlemler ve analizler değişiktir.
İsimsel ölçekte verilerde sayılar sadece birbirinden karşılıklı ayrılık gösteren kategorilere verilen adlardır ve bu isim/sayı sırası ve aralığı veya orijini için hiçbir matematiksel özellik yoktur. Bu çeşit ölçekte verilere ancak çok zayıf istatistik betimleyici ölçüler ve çıkarımsal analizler uygulanabilir.
Sırasal ölçek verilerdeki sayılar birbirinden karşılıklı ayrantılı kategorilere isim verdiği gibi, bu kategoriler arasındaki rütbe ve sıralı düzeni de açıklarlar. Sayı değerleri arasındaki sırasal düzen değiştirilemeden her kategoriye atıf edilen gerçek sayı değiştirilebilir (yani monotonik dönüşüm uygulanabilir.) Sayılar arasında büyüklük farkı önemli olmadığı için değişik kategori sayıları üzerinde uygulanan bir basit aritmetik işlem (toplama, çıkarma, çarpma veya bölme) anlamsız sonuçlar verebilir.
Aralıksal ölçekte veri sayıları gerçekten sayı olup aralarındaki değişikler basit aritmetik işlem için bile anlamlıdır. Ancak aralıksal ölçekde veri değerleri için sayıların başlama orijini (yani 0 değer) keyfidir. Örneğin ısı derecesi olarak elde edilen veriler aralıksaldır. Ölçüm ölçeği santigrad olabilir; ancak değişik 0 orijin değerleri olan fahrenhayt da olabilirler.
Oransal ölçekte veriler hem değişik ölçülmeler arasında farklar anlamlıdır ve hem de bunlar için gerçek bir 0 başlangıç noktası mevcuttur. Yine ısi derecesi örneği verilirse Kelvin derecesi oransal ölçektedir; çünkü orijin (-273 °C mutlak sıfır) 0°Kelvin olur; bu bir gerçek ) noktasıdır ve bu ısı derecesi altında ısı olamaz.
İsimsel veya sırasal ölçekle ölçülen değişkenler için veriler birlikte kategorik değişkenler olarak anılmakta ve aralıksal veya oransal ölçekte olan veriler kantitatif niceliksel değişkenler olarak adlandırılmaktadır.
Bilgisayar ile istatistiksel araştırma
20. yüzyılın ikinci yarısında bilgisayarların hesaplama gücü ve hızının inanılamayacak bir şekilde artması ve bilgisayar kullanımı yaygın bir hale gelmesi istatistik biliminin pratik uygulaması ve hatta teorik gelişmesi üzerine çok büyük etki yapmıştır. Pratik istatistik hesaplamanın çok zor olması dolayısıyla veri analizi devamlı olarak hesaplamanın kolaylaştırılması üzerine odaklanıp daha çok doğrusal modellere dayanmıştır. Çok yaygın kullanılan ve çok güçlü bilgisayarların kullanılmaya başlanılması ve sayısal algoritmaların geliştirilip bilgisayar yazılımları geliştirilmesi ile yeni doğrusal olmayan modeller (örneğin doğrusal olmayan regreyon, genelleştirilmiş doğrusal modeller, çok-seviyeli model gibi) pratikte kullanılmaya başlanmıştır.
Bilgisayar devrimi tekrar örnekleme yöntemi, özyükleme yöntemleri, Gibbs örneklemesi, permütasyon testleri gibi çok bilgisayara dayanan teknikler kullanılmaya başlamıştır. Diğer taraftan istatistik gibi temeli ileri matematiğe bağlı olmayan ve büyük bilgisayar gücüne dayanan (yapay sinir ağları veya veri madenciliği gibi) araştırma ve pratik veri inceleme yöntemleri gelişmiştir.
İstatistik biliminin geleceği 20. yüzyıl başındaki teorik gelişmelerden sonra, daha empirik ve pratik bir yaklaşım haline gelmektedir. Bu yaklaşımda genel hesaplama yazılım ve paketlere istatistik yöntemlerinin eklenmeleri (örneğin kutuzzilim programlarının istatistiksel bölümleri) ve özel şekil de hazırlanmış istatistiksel paketlerinin yaygın şekilde kullanılabilmesi büyük bir rol oynayacağı şüphesizdir.
İstatistiğin yanlış kullanılması
İstatistiğin yanlış kullanılması güç fark edilen ama çok ciddi tanımlama ve açıklama hataları ortaya çıkarabilir. Bu hatalar ciddidir çünkü ortaya yıkıcı hatalı kararlar çıkabilir. Örneğin sosyal siyaset, doktorluk ve tıp uygulamaları, köprüler gibi yapılar için yapısal güvenilirlik için veriler hep istatistiğin hatasız uygun şekilde kullanılmasına dayanır.
İstatistik doğru olarak uygulansa bile bu konu üzerinde pek az bilgi ve tecrübesi olanların istatistiksel sonuç çıkarımlarını yorumlayıp açıklaması çok zor olabilir. Veri setindeki bir trendin istatistiksel anlamlılığının (yani trendin bir örneklemde her ne kadar rastgele değişim tarafından ortaya çıkacağını açıklanabileceğinin) incelenmesi, bu anlamlılık kavramının sezgi yoluyla ortaya çıkmasıyla aynı olabildiği gibi, çok kere de değişiktir. Bu demektir ki sezgiye dayanan çıkarımlar uygun olmayan kararlara yol açabilir. Kişilerin istatiksel cahilliğinden ayrılıp günlük yaşamlarında veriler ve enformasyon ile uygun şeklide uğraşmaları için yeterli derecede istatistiksel beceriye sahip olmaları (ve yeter derecede kuşkulu olmaları) için hiç olmazsa düşük bir seviyede istatistik eğitiminden geçmeleri ve istatistiksel okur-yazarlık niteliği kazanmaları gerekir.
İstatistik bilgisinin hatalı ve yanlış kullanıldığına dair epeyce geniş bir algı bulunmaktadır. Bu yetmezmiş gibi, çok kere yapılan hataların ve yanlış kullanılmanın bilinçli ve kasıtlı yapıldığı hissi doğmaktadır. Hatalı analiz sonucu alınan kararın istatistiksel sonuçları sunan kişiye yarar sağlayabilabilmesi imkanı olduğu bilinmektedir. Bir 19. yüzyıl İngiliz başbakanı olan Benjamin Disraeli'ye atıf edilen "Üç türlü yalan bulunmaktadır: yalanlar, lanetli yalanlar ve istatistikler." cümlesi nerede ise atasözü gibi kullanılmaktadır. Amerikan Harvard Üniversitesi Başkanı "Lawrence Lovell" 1909’da istatistik "börek gibidir ve ancak kimin tarafından yapıldığı bilinirse ve içindekilerden insan emin olabilirse o zaman tatmin edicidir" sözleri de bu kasıtlı bilinçli istatistik hatası yapma algısına biraz daha açıklama katar.
Kaynakça
- Şener Büyüköztürk vd. (2009), Sosyal Bilimler İçin İstatistik, Ankara : Pegem Akademi, s. 1-2.
- ISIS (Uluslararasi Istatistik Enstitüsü), ISI Çoklu Dilli İstatistiksel Terimler Lugati (Multilingual Glossary of Statistical Terms) Türkçe
| ||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||