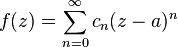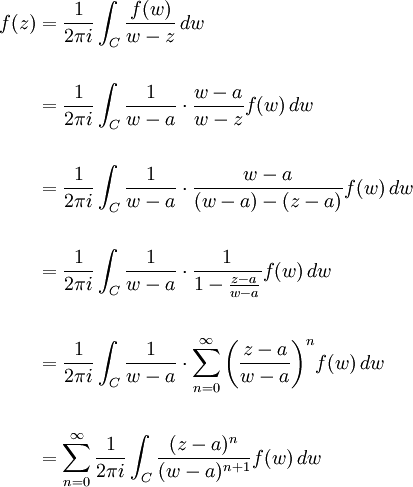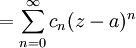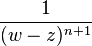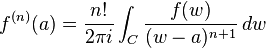Holomorf fonksiyonların analitikliği

Matematiğin bir alanı olan karmaşık analizde, karmaşık değişkenli ve karmaşık değerler alan bir f fonksiyonu

• bir a noktasında holomorfsa, a noktası etrafındaki açık bir komşuluk içindeki her noktada türevlenebilirdir. Aynı zamanda ters ifade de doğrudur: fonksiyon a noktası etrafındaki bir açık komşuluk içindeki her noktada türevlenebilir ise, fonksiyon a noktasında holomorftur.

• bir a noktası etrafında yakınsak bir kuvvet serisi olan

$f(z)=\sum_{n=0}^\infty c_n(z-a)^n$

şeklinde açılıyorsa, fonksiyon a noktasında analitiktir.(bu durum yakınsaklık yarıçapının pozitif olduğu gösterir.)

Karmaşık analizin önemli teoremlerinden birisi de holomorf fonksiyonların analitik olmasıdır. Bu teoremin sonuçlarından bazıları ise şunlardır:

• İki holomorf fonksiyon, fonksiyonların tanım kümelerinin kesişimi içinde yığılma noktası olan sonsuz bir kümeye ait olan her noktada aynı değerleri alıyorsa, aynı zamanda belli bir açık küme içindeki her yerde de aynı değerleri alıyordur. Bu özellik aslında özdeşlik teoreminin bir iyileştirilmesidir.

• Kuvvet serileri sonsuz kere türevlenebilir olduğu için, holomorf fonksiyonlar da aynı özelliğe sahiptir.

• Yakınsaklık yarıçapı, her zaman, merkez olan a noktasından fonksiyonun en yakın tekilliğine olan uzaklığa eşittir. Eğer fonksiyonun tekilliği yoksa, yani fonksiyon tam bir fonksiyonsa, o zaman yakınsaklık yarıçapı sonsuzdur. Aslında daha düzgün bir ifadeyle, bu, teoremin doğrudan sonucu değildir ancak yan ürün olarak sayılabilir.

• Karmaşık analizde tam olan bir tümsek (bump) fonksiyon yoktur. Bilhassa, karmaşık düzlemin herhangi bağlantılı açık bir kümesinde, bu küme üzerinde tanımlanmış holomorf bir tümsek fonksiyon olamaz. Birimin parçalanışını olanaksızlaştırdığı için, bu durumun karmaşık çokkatlıların çalışılmasında birçok dallanması vardır. Aksine, birimin parçalanışı herhangi gerçel bir çokkatlıda kullanılabilen bir araçtır.

Kanıt

İlk kez Cauchy tarafından verilen argüman, Cauchy integral formülü ve

$1 \over w-z .$

ifadesinin kuvvet serisi açılımına dayanmaktadır.

f, a merkezli açık bir diskin her yerinde türevli olsun. z de bu açık diskte olsun. C ise bu diskin içinde a merkezli, yarıçapı z 'nin a 'ya uzaklığından daha fazla olan pozitif yönlü (yani saat yönünün tersi yönlü) olan bir çember olsun. Cauchy integral formülünden başlarsak,

$\begin{align}f(z) &{}= {1 \over 2\pi i}\int_C {f(w) \over w-z}\,dw \\ \\ &{}= {1 \over 2\pi i}\int_C {1 \over w-a}\cdot{w-a \over w-z}f(w)\,dw \\ \\ &{}= {1 \over 2\pi i}\int_C {1 \over w-a}\cdot{w-a \over (w-a)-(z-a)}f(w)\,dw \\ \\ &{}={1 \over 2\pi i}\int_C {1 \over w-a}\cdot{1 \over 1-{z-a \over w-a}}f(w)\,dw \\ \\ &{}={1 \over 2\pi i}\int_C {1 \over w-a}\cdot{\sum_{n=0}^\infty\left({z-a \over w-a}\right)^n} f(w)\,dw \\ \\ &{}=\sum_{n=0}^\infty{1 \over 2\pi i}\int_C {(z-a)^n \over (w-a)^{n+1}} f(w)\,dw\end{align}$

sonucuna varırız.

Burada toplam ve integralin yer değişimi, geometrik serinin, yakınsaklık diskinin içindeki sınırdan uzak sınırlı altkümeler içindeki düzgün sürekliliği tarafından sağlanmaktadır. (z - a)ⁿ çarpanı w üzerinden alınan integrale bağlı olmadığından, çarpan dışarıya alınabilir:

$=\sum_{n=0}^\infty (z-a)^n {1 \over 2\pi i}\int_C {f(w) \over (w-a)^{n+1}} \,dw.$

İntegral ve 1/(2πi) çarpanı z değişkenine bağlı olmadığından, yani z 'nin fonksiyonları olmadıklarından, tüm ifade bir sabit c_n olur. Yani

$=\sum_{n=0}^\infty c_n(z-a)^n$

ifadesini yazabiliriz ki bu da istenen kuvvet serisidir.

Notlar

• Kuvvet serileri terim bazında türevlenebilir olduğu için, yukarıdaki tartışma tersi yönde yapılırsa ve

$1 \over (w-z)^{n+1}$

kuvvet serisi kullanılırsa

$f^{(n)}(a) = {n! \over 2\pi i} \int_C {f(w) \over (w-a)^{n+1}}\, dw$

elde edilir. Bu türevler için Cauchy integral formülüdür. Bu yüzden, elde edilen kuvvet serisi, f 'nin Taylor serisidir.

• Bu argüman, merkez olan a noktasına f 'nin herhangi bir tekilliğinden daha yakın olan herhangi bir z noktası için doğrudur. Bu yüzden, Taylor serisinin yakınsaklık yarıçapı, a 'ya en yakın tekillik noktasının a noktasına olan uzaklığından daha daha küçük olamaz.(daha büyük de olamaz çünkü kuvvet serilerinin yakınsaklık çemberlerinin içinde tekillik noktaları yoktur).

• Özdeşlik teoreminin özel bir durumu takip eden nottan çıkar. Eğer iki holomorf fonksiyon a noktasının etrafındaki (muhtemelen çok küçük) açık bir U komşuluğunda aynı değerleri alıyorsa, o zaman ikisi de d 'nin en yakın tekillikten a 'ya olan uzaklığı gösterdiği B_d(a) açık kümesinde de aynı değerleri alır.

Dış bağlantılar

• PlanetMath