Levi-Civita sembolü

Levi-Civita bağlantısı ile karıştırılmamalıdır.

bakınız Ricci hesabı, Einstein gösterimi, ve yükseltme ve indirme indisleri için indis gösterimi yazı içinde kullanılıyor.

matematikte, özel olarak doğrusal cebirde, tensör analizi, ve diferansiyel geometri,Levi-Civita sembolü sayıların bir koleksiyonunun gösterimidir;bazı pozitif tamsayı n için doğal sayıların 1, 2, …, n bir permütasyonun işaretinden tanımlanır. Bu adını Italyan matematikçi ve fizikist Tullio Levi-Civitadan alır. Diğer adı permutasyon sembolü içerdiğinden , antisimetrik sembol, veya dalgalı sembol, bu antisimetrik özelliklere kaynaktır ve permutasyonların terimleri içinde tanımlanıyor.

Levi-Civita sembolündeki ifadesine standard harfler yunan alt indis epsilon ε veya ϵ, veya Latin alt indis e daha az yaygındır.Tensor analizi ile uyumlu bir yol içinde permütasyonu görüntüsüne indis gösterimi tek olanak sağlar:

${\displaystyle \varepsilon _{i_{1}i_{2}\cdots i_{n}}}$

burada her i₁, i₂, …, i_n indisi 1, 2, …, n değeri alıyor.Burada bir n-boyutlu dizi içinde düzenlenebilir nⁿ ${\displaystyle \varepsilon _{i_{1}i_{2}\cdots i_{n}}}$'ın indis değerleri vardır. sembolün özellikleri anahtar tanımı tüm indis içindeki toplam antisimetridir.Her iki indis birbiriyle yer değiştirildiğinde, eşit ya da değil, sembol olumsuzlanır:

${\displaystyle \varepsilon _{\cdots i_{p}\cdots i_{q}\cdots }=-\varepsilon _{\cdots i_{q}\cdots i_{p}\cdots }.}$

Eğer herhangi iki indisler eşitleniyor,ise sembol sıfırdır. O zaman tüm indisler eşit değildir, elimizde olan:

${\displaystyle \varepsilon _{i_{1}i_{2}\cdots i_{n}}=(-1)^{p}\varepsilon _{12\cdots n},}$

burada p (permutasyonun kesri denir) i₁ deşifreye gerekli indislerin yer değiştirmelerinin sayılarıdır, i₂, …, i_n 1, 2, …, n,sıralaması içinde ve (−1)^p faktörü permutasyonun işareti veya imzası denir. ε_12…n değerleri olarak tanımlanıyor,başka tüm permütasyon sembolünün özel değerleri belirsizdir vardır.. Çoğu yazarlarε_12…n = +1 tümü eşitsizlik olduğunda,bunun anlamı Levi-Civita sembolünün bir permutasyonunun işareti eşittir demektir eşitsizliklerdir. Bu seçim, bu yazı boyunca kullanılır.

aslında n sembolu üzerinde indislerin sayılarıyla "n-boyutlu Levi-Civita sembolü" ne kaynak ve soru içinde uygun vektör uzayının,boyutluluğu bu Öklidyen veya non-Öklidyen eşleşebilir, saf uzay veya uzayzaman. Levi-Civita sembolünün değerleri herhangi metrik tensör ve koordinat sisteminden bağımsızdır

3d Öklid uzayı içinde iki vektörlerin çapraz çarpımı ve Levi-Civita sembolü bir kare matrisin determinantının ifadesine kullanılabilir.

Tanım

Levi-Civita sembolünün ortak boyutluluk 3d içindedir ve 4d, ve 2d'ye bazı uzantılar,böylece önceki bu tanımları bir boyutların herhangi sayıları içinde görmek için yararlıdır .

İki boyutlular

iki-boyutlu Levi-Civita sembolü ile tanımlanıyor:

${\displaystyle \varepsilon _{ij}={\begin{cases}+1&{\text{eğer }}(i,j){\text{ ise }}(1,2)\\-1&{\text{eğer }}(i,j){\text{ ise }}(2,1)\\\;\;\,0&{\text{eğer }}i=j\end{cases}}}$

Değerler bir 2 × 2 antisimetrik matris içinde düzenlenebilir:

${\displaystyle {\begin{pmatrix}\varepsilon _{11}&\varepsilon _{12}\\\varepsilon _{21}&\varepsilon _{22}\end{pmatrix}}={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}}$

supersimetri gibi belli özel konular içinde olmasına rağmen 2d sembolünün kullanımı oldukça nadirdir^[1] ve twistor teorisi^[2] bu 2-spinorlerin kavramı içinde görüntülenir 3d ve daha yüksek-boyutlu Levi-Civita sembolleri daha yaygın kullanılıyor.

Üç boyutlar

ε_ijk içindeki (i, j, k) indisler için, ε = +1'ya karşılık döngüsel sıra (1,2,3) (sarı) içinde 1, 2, 3 değerinden oluşur , ε = −1, diğerleri ε = 0'ya karşılık ters döngüsel sıra (kırmızı) içinde meydana geldiğinde.

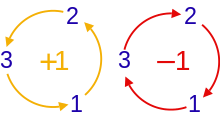
üç boyutlu içinde,Levi-Civita sembolü aşağıdakiler olarak tanımlanıyor:^[3]

${\displaystyle \varepsilon _{ijk}={\begin{cases}+1&{\text{eğer}}(i,j,k){\text{ ise }}(1,2,3),(3,1,2){\text{ veya }}(2,3,1),\\-1&{\text{eğer}}(i,j,k){\text{ ise }}(1,3,2),(3,2,1){\text{ veya }}(2,1,3),\\\;\;\,0&{\text{eğer}}i=j{\text{ veya }}j=k{\text{ veya }}k=i\end{cases}}}$

yani ${\displaystyle \varepsilon _{ijk}}$ 1'dir eğer (i, j, k) ,(1,2,3)'ün bir çift permutasyonu , −1 eğer bu bir tek permutasyon ise, ve herhangi bir indis yinelenirse 0'dır.üç boyutlular içinde, ve yüksek değil, (1,2,3)'ün siklik permutasyonları tüm çift permutasyonlardır ve benzer antisiklik permutasyonlar tüm tek permutasyonlardır. Bunun anlamı 3d içinde bu siklik almak için yeterlidir veya (1,2,3)'ün permutasyonları antisikliktir ve kolay elde edilen tüm çift veya tek permutasyonlardır.

2d matrislere analogtur,3d Levi-Civita sembolünün değeri bir 3×3×3 dizisi içinde düzenlenebilir:

burada i derinliktir, j satır ve k sütun.

Bazı örnekler:

${\displaystyle \varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{2}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}}=-1}$

${\displaystyle \varepsilon _{\color {Violet}{3}\color {BrickRed}{1}\color {Orange}{2}}=-\varepsilon _{\color {Orange}{2}\color {BrickRed}{1}\color {Violet}{3}}=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}})=1}$

${\displaystyle \varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {BrickRed}{1}}=-\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{2}}=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{2}\color {Violet}{3}})=1}$

${\displaystyle \varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {Orange}{2}}=-\varepsilon _{\color {Orange}{2}\color {Violet}{3}\color {Orange}{2}}=0}$

Dört boyutlular

dört boyutlular içinde,Levi-Civita sembolü olarak tanımı:

${\displaystyle \varepsilon _{ijkl}={\begin{cases}+1&{\text{eğer }}(i,j,k,l){\text{ bir çift permütasyondur }}(1,2,3,4)\\-1&{\text{eğer }}(i,j,k,l){\text{ bir tek permütasyondur }}(1,2,3,4)\\0&{\text{diğerleri}}\end{cases}}}$

Bu değerler bir 4×4×4×4 dizi içinde düzenlenebilir,4d içindekine rağmen ve bu yüksekliği çizmek zordur.

Bazı örnekler:

${\displaystyle \varepsilon _{\color {BrickRed}{1}\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}}=-1}$

${\displaystyle \varepsilon _{\color {Orange}{\color {Orange}{2}}\color {BrickRed}{1}\color {Violet}{3}\color {RedViolet}{4}}=-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}}=-1}$

${\displaystyle \varepsilon _{\color {RedViolet}{4}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {BrickRed}{1}}=-\varepsilon _{\color {BrickRed}{1}\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}}=-(-\varepsilon _{\color {BrickRed}{1}\color {Orange}{\color {Orange}{2}}\color {Violet}{3}\color {RedViolet}{4}})=1}$

${\displaystyle \varepsilon _{\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}\color {Violet}{3}}=-\varepsilon _{\color {Violet}{3}\color {Orange}{\color {Orange}{2}}\color {RedViolet}{4}\color {Violet}{3}}=0}$

n boyutlulara genelleştirme

Levi-Civita sembolü n boyutlu'ya genelleştirilebilir:^[4]

${\displaystyle \varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}={\begin{cases}+1&{\text{eğer }}(a_{1},a_{2},a_{3},\ldots ,a_{n}){\text{ bir çift permütasyondur }}(1,2,3,\dots ,n)\\-1&{\text{eğer }}(a_{1},a_{2},a_{3},\ldots ,a_{n}){\text{ bir tek permutasyondur }}(1,2,3,\dots ,n)\\0&{\text{diğerleri}}\end{cases}}}$

Böylece bu bir permutasyonun durumu içinde permutasyonun işareti'dir ve diğerleri sıfır.

sayıların düzgün çarpımı için büyük Pi gösterimi ${\displaystyle \prod }$ kullanılıyor,bir sembol için açık ifadedir:

${\displaystyle {\begin{aligned}\varepsilon _{a_{1}a_{2}a_{3}\ldots a_{n}}&=\prod _{1\leq i<j\leq n}\operatorname {sgn}(a_{j}-a_{i})\\&=\operatorname {sgn}(a_{2}-a_{1})\operatorname {sgn}(a_{3}-a_{1})\ldots \operatorname {sgn}(a_{n}-a_{1})\operatorname {sgn}(a_{3}-a_{2})\operatorname {sgn}(a_{4}-a_{2})\ldots \operatorname {sgn}(a_{n}-a_{2})\ldots \operatorname {sgn}(a_{n}-a_{n-1})\end{aligned}}}$

burada çarpım tüm indisler içinde toplam antisimetriktir, ve işaret fonksiyonu ("sgn" ile ifade ediliyor) atılan her farkın the mutlak değer işareti özütler. Formül tüm indis değeri ve herhangi n için doğrudur(n = 1 ise veya 0, bu boş çarpımdır). Bunun için, nadiren bu pratik içinde kullanılan değişimci indisler daha hızlıdır.

Özellikler

Bir tensör böyle bir ortonormal taban içinde bileşenler ( eşdeğişken rank n'in bir tensörüdür) ile veriliyor bazen bir permutasyon tensör denir.Bu aslında bir psödotensör için jakobiyen determinant −1'ın bir ortogonal dönüşüm altında (yani,bir yansıma ile bir dönme düzeni), bu bir küçük işaret kazanıyor.Levi-Civita sembolü olarak bir psödotensördür,alma sonucu bir çapraz çarpım bir psödovektordür,bir vektör değil.^[5]

Genel bir koordinat değişikliği altında,permutasyonun bileşenleri tensör dönüşüm matrisinin jakobiyeni ile çarpılıyor. Bu ifade bu koordinat çerçevesi içinde tek bu tensör içindeki farktan tanımlanıyor idi, bu bileşenler can differ from those of the by bir tüm faktör ile Levi-Civita sembolü tarafından. Eğer çerçeve ortonormaldir,faktor çerçevenin uyumu olup olmadığı üzerinden ±1 bağlı olacak aynı veya değildir.^[5]

indis-serbest içinde tensör gösterimi,Levi-Civita sembolü Hodge ikilisinin kavramı ile yer değiştirir.

burada tensör indis gösteriminin bir kavramı içinde tensör bileşenlerin manipülasyonuna kullanılıyor,Levi-Civita sembolü ile bu indisler ya altsimge veya üstsimge olarak yazılabilmesi ile anlamı içinde değişiklik yok, gibi uygun olabilir. Böylece, tek yazılabilen

${\displaystyle \varepsilon ^{ij\dots k}=\varepsilon _{ij\dots k}.}$

bu örnekler içinde, üstsimge altsimge ile eşdeğer düşünülebilir.

Toplam semboller kullanılan Einstein gösterimi ile elenebilir, burada bir indis arasında tekrarlanan iki veya bu indis üzerinde daha fazla terimler toplamını gösterir.Örneğin

${\displaystyle \varepsilon _{ijk}\varepsilon ^{imn}\equiv \sum _{i=1,2,3}\varepsilon _{ijk}\varepsilon ^{imn}}$.

aşağıdaki örnek içinde, Einstein gösterimi kullanılıyor.

İki boyutlular

iki boyutlular içinde, o zaman tüm i, j, m, n her 1 ve 2 değeri alınır,^[3]

   

${\displaystyle \varepsilon _{ij}\varepsilon ^{mn}=\delta _{i}{}^{m}\delta _{j}{}^{n}-\delta _{i}{}^{n}\delta _{j}{}^{m}}$

(Kaynak denklem-1)

   

   

${\displaystyle \varepsilon _{ij}\varepsilon ^{in}=\delta _{j}{}^{n}}$

(Kaynak denklem-2)

   

   

${\displaystyle \varepsilon _{ij}\varepsilon ^{ij}=2.}$

(Kaynak denklem-3)

   

Üç boyutlular

İndis ve sembol değerleri

üç boyutlular içinde, o zaman tüm i, j, k, m, n her 1, 2, ve 3 alınan değerleri:^[3]

   

${\displaystyle \varepsilon _{ijk}\varepsilon ^{imn}=\delta _{j}{}^{m}\delta _{k}{}^{n}-\delta _{j}{}^{n}\delta _{k}{}^{m}}$

(Kaynak denklem-4)

   

   

${\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=2\delta _{j}^{i}}$

(Kaynak denklem-5)

   

   

${\displaystyle \varepsilon _{ijk}\varepsilon ^{ijk}=6.}$

(Kaynak denklem-6)

   

Çarpımlar

Levi-Civita sembol Kronecker delta'ya ilişiktir.üç boyutlular içinde,ilişkililik aşağıdaki denklemler ile verilir (dik çizgi determinant ifadesi):^[4]

${\displaystyle {\begin{aligned}\varepsilon _{ijk}\varepsilon _{lmn}&={\begin{vmatrix}\delta _{il}&\delta _{im}&\delta _{in}\\\delta _{jl}&\delta _{jm}&\delta _{jn}\\\delta _{kl}&\delta _{km}&\delta _{kn}\\\end{vmatrix}}\\&=\delta _{il}\left(\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}\right)-\delta _{im}\left(\delta _{jl}\delta _{kn}-\delta _{jn}\delta _{kl}\right)+\delta _{in}\left(\delta _{jl}\delta _{km}-\delta _{jm}\delta _{kl}\right).\end{aligned}}}$

Bu sonucun bir özel durumu (4)dür:

${\displaystyle \sum _{i=1}^{3}\varepsilon _{ijk}\varepsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}}$

bazen "büzülme epsilon eşitliği" kodlanır.

Einstein gösterimi içinde,i üzerinde toplam ifadesi i indisinin çiftidir. Önceki ardından belirtilir: ${\displaystyle \varepsilon _{ijk}\varepsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}\,.}$

${\displaystyle \sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{ijk}\varepsilon _{ijn}=2\delta _{kn}}$

n boyutlular

indis ve sembol değerleri

n boyutular içinde, o zaman tüm i₁,...,i_n, j₁,...,j_n 1, 2,..., n alınan değerleri:

   

${\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{j_{1}\dots j_{n}}=n!\delta _{[i_{1}}{}^{j_{1}}\dots \delta _{i_{n}]}{}^{j_{n}}=\delta _{i_{1}\dots i_{n}}^{j_{1}\dots j_{n}}}$

(Kaynak denklem-7)

   

   

${\displaystyle \varepsilon _{i_{1}\dots i_{k}~i_{k+1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{k}~j_{k+1}\dots j_{n}}=k!(n-k)!~\delta _{[i_{k+1}}{}^{j_{k+1}}\dots \delta _{i_{n}]}{}^{j_{n}}=k!~\delta _{i_{k+1}\dots i_{n}}^{j_{k+1}\dots j_{n}}}$

(Kaynak denklem-8)

   

   

${\displaystyle \varepsilon _{i_{1}\dots i_{n}}\varepsilon ^{i_{1}\dots i_{n}}=n!}$

(Kaynak denklem-9)

   

burada ünlem işareti (!) faktöriyel ifadesi, ve δα…β… genelleştirilmiş Kronecker deltadır.Herhangi n için, özellik

${\displaystyle \sum _{i,j,k,\dots =1}^{n}\varepsilon _{ijk\dots }\varepsilon _{ijk\dots }=n!}$

bu çarpanlardan aşağıda

• her permütasyon ya çift veya tektir,
• (+1)² = (−1)² = 1, ve
• herhangi n-küme elemanı sayısının permutasyonunun sayısı n! tamlıktır.

Çarpımlar

Genel içinde,n boyutlular için, tek iki Levi-Civita sembollerinin çarpımı yazılabilir:

${\displaystyle \varepsilon _{i_{1}i_{2}\dots i_{n}}\varepsilon _{j_{1}j_{2}\dots j_{n}}={\begin{vmatrix}\delta _{i_{1}j_{1}}&\delta _{i_{1}j_{2}}&\dots &\delta _{i_{1}j_{n}}\\\delta _{i_{2}j_{1}}&\delta _{i_{2}j_{2}}&\dots &\delta _{i_{2}j_{n}}\\\vdots &\vdots &\ddots &\vdots \\\delta _{i_{n}j_{1}}&\delta _{i_{n}j_{2}}&\dots &\delta _{i_{n}j_{n}}\\\end{vmatrix}}}$.

Kanıtlar

Denklem Notu-1 için, iki yüz ij ve mn nin sırasıyla antisimetriktir. Biz bunun için yalnızca i ≠ j ve m ≠ n durumunu düşünmeye gerek var. Yerine koyma ile, biz bu denklem ${\displaystyle \varepsilon _{12}\varepsilon ^{12}}$ için tutulduğunu görüyoruz, yani i = m = 1 ve j = n = 2 için. (iki yüz tek ise ). Ötesi denklem ij ve mn içinde ,yukardaki duruma (hangisi tutulursa) indirgenebilen bu değerlerin herhangi kümesi için antisimetriktir. Denklem böylece ij ve mn nin tüm değerleri için tutulur.

Denklem Notu-1 i kullanıyoruz, elimizdeki Denklem Notu-2 için

${\displaystyle \varepsilon _{ij}\varepsilon ^{in}=\delta _{i}{}^{i}\delta _{j}{}^{n}-\delta _{i}{}^{n}\delta _{j}{}^{i}=2\delta _{j}{}^{n}-\delta _{j}{}^{n}=\delta _{j}{}^{n}\,.}$

Burada biz Einstein toplam kuralı ile i kullanıyoruz 1 den 2'ye gidiyor. Sonuç,Denklem Notu-3 Denklem Notu-2dan benzerlik aşağıdadır.

Denklem Notu-5 kurmak için, unutmadan her iki taraf kayboluyor eğer i ≠ j. Yani, eğer i ≠ j, ise m ve n birini seçemezsiniz böylece her iki permutasyon semboller sol üzerinde sıfır olmayandır. İse, i ≠ j ile sabitlenir, burada yalnız m ve n kalan iki indislerden seçmek için iki yollardır.Herhangi bu gibi indisler için, elimizde

${\displaystyle \varepsilon _{jmn}\varepsilon ^{imn}=(\varepsilon ^{imn})^{2}=1}$

(toplam yok), ve sonuç aşağıdadır.

İse(Denklem Notu-6) beri takip ise 3! = 6 ve i, j, k herhangi farklı indisleri için 1, 2, 3,değerleri alıyor, elimizde olan

${\displaystyle \varepsilon _{ijk}\varepsilon ^{ijk}=1}$ (toplam yok, ayrı ayrı i, j, k ).

Uygulamalar ve örnekler

Determinantlar

Doğrusal cebir içinde,bir 3 × 3 kare matris A = (a_ij)'nın determinantı yazılabilir^[6]

${\displaystyle \det(\mathbf {A} )=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}a_{1i}a_{2j}a_{3k}}$

bir n × n matris A = (a_ij)'nın determinantı benzer olarak yazılabilir^[5]

${\displaystyle \det(\mathbf {A} )=\varepsilon _{i_{1}\cdots i_{n}}a_{1i_{1}}\cdots a_{ni_{n}},}$

burada her i_r 1,..., n üzerinde özetlenebilir olmalıdır, veya eşitliği:

${\displaystyle \det(\mathbf {A} )={\frac {1}{n!}}\varepsilon _{i_{1}\cdots i_{n}}\varepsilon _{j_{1}\cdots j_{n}}a_{i_{1}j_{1}}\cdots a_{i_{n}j_{n}},}$

burada şimdi her i_r ve her j_r 1,.., n üzerinde özetlenebilir olmalıdır. Daha geneli, elimizdeki eşitlik^[5]

${\displaystyle \sum _{i_{1},i_{2},\dots }\varepsilon _{i_{1}\cdots i_{n}}a_{i_{1}\,j_{1}}\cdots a_{i_{n}\,j_{n}}=\det(\mathbf {A} )\varepsilon _{j_{1}\cdots j_{n}}}$

Vektör çapraz çarpımı

Çapraz çarpım (iki vektörler)

Eğer a = (a¹, a², a³) ve b = (b¹, b², b³) ${\displaystyle \mathbb {R} ^{3}}$ içinde vektörlerse (bazı sağ-taraf koordinat sistemi içinde gösterilen bir ortonormal taban kullanılıyor), burada çapraz çarpım bir determinant olarak yazılabilir:^[5]

${\displaystyle \mathbf {a\times b} ={\begin{vmatrix}\mathbf {e_{1}} &\mathbf {e_{2}} &\mathbf {e_{3}} \\a^{1}&a^{2}&a^{3}\\b^{1}&b^{2}&b^{3}\\\end{vmatrix}}=\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}\mathbf {e} _{i}a^{j}b^{k}}$

Bundan dolayı ayrıca Levi-Civita sembolü kullanılıyor, ve daha basitçe:

${\displaystyle (\mathbf {a\times b} )_{i}=\sum _{j=1}^{3}\sum _{k=1}^{3}\varepsilon _{ijk}a^{j}b^{k}.}$

Einstein gösterimi içindi, toplam sembolleri atlanabilir, ve burada çapraz çarpım eşitliğinin iinci bileşenleri ^[4]

${\displaystyle (\mathbf {a\times b} )_{i}=\varepsilon _{ijk}a^{j}b^{k}.}$

ilk bileşenler

${\displaystyle (\mathbf {a\times b} )_{1}=a^{2}b^{3}-a^{3}b^{2}\,,}$

ise 1, 2, 3'ün döngüsel permütasyonu ile diğerleri hemen türetilebilir olsun,yukarıdaki formüllerde açık bir şekilde onları hesaplamadan:

${\displaystyle (\mathbf {a\times b} )_{2}=a^{3}b^{1}-a^{1}b^{3}\,,}$

${\displaystyle (\mathbf {a\times b} )_{3}=a^{1}b^{2}-a^{2}b^{1}\,.}$

Üçlü skaler çarpım (üç vektörler)

çapraz çarpım için, elimizde olan yukardaki bağıntılardan:

${\displaystyle \mathbf {a\times b} =-\mathbf {b\times a} }$.

Eğer c = (c¹, c², c³) diğer vektörler, ise üçlü skalar çarpım eşittir

${\displaystyle \mathbf {a} \cdot (\mathbf {b\times c} )=\varepsilon _{ijk}a^{i}b^{j}c^{k}.}$

bu ifadelerden, bu üçlü skaler çarpımın antisimetrik olduğu bileşenlerin herhangi çiftini değiştirirken görülebilir. Örneğin,

${\displaystyle \mathbf {a} \cdot (\mathbf {b\times c} )=-\mathbf {b} \cdot (\mathbf {a\times c} )}$.

Curl (tek vektör alanı)

Eğer F = (F¹, F², F³) x = (x¹, x², x³) (Kartezyen koordinatlar kullanılıyor) pozisyonunun bir fonksiyonu olarak ${\displaystyle \mathbb {R} ^{3}}$ nın bazı açık küme üzerinde bir vektör alanı tanımlanıyor,ise F in curl 'unun i.inci bileşenleri eşittir.^[4]

${\displaystyle (\nabla \times \mathbf {F} )^{i}(\mathbf {x} )=\varepsilon ^{ijk}{\frac {\partial }{\partial x^{j}}}F^{k}(\mathbf {x} ),}$

Bu aşağıdaki çapraz çarpım ifadesinden yukarıda,gradyan vektör operatörün bileşenleri yerini alır (nabla).

Tensör yoğunluğu

Herhangi keyfi eğrisel koordinat sistemi içinde ve manifold üzerinde bir metrikin yokluk içinde çift, yukarda tanım olarak Levi-Civita sembolü iki farklı yollar içinde bir tensör yoğunluğu alanı olarak kabul edilebilir.Bu bir karşıtdeğişir tensör yoğunluğu olarak +1 ağırlığın veya −1 ağırlığın bir eşdeğişir tensor yoğunluğu olarak kabul edilebilir.n içinde kullanılan boyutları genelleştirilmiş Kronecker deltadır,^[7]

${\displaystyle \varepsilon ^{\mu _{1}\cdots \mu _{n}}=\delta _{\,1\,\cdots \,n}^{\mu _{1}\cdots \mu _{n}}\,}$

${\displaystyle \varepsilon _{\nu _{1}\cdots \nu _{n}}=\delta _{\nu _{1}\cdots \nu _{n}}^{\,1\,\cdots \,n}\,.}$

dikkat edin bu sayısal eşliktir. Özel olarak, işaret aynıdır.

Mutlak tensör

Bir metrik tensör alanının varlığında,bir koordinat sistemi tanjant uzayı tabanında bu metriğe sırasıyla ortonormal olduğundan bu tür nerede olarak olursa olsun Levi-Civita sembolü kabulü ile mutlak koveryant kontravaryant ve tensör alanlarını tanımlayabilir. Bu mutlak tensör alanları ile ve ne de yukarıda belirtilen tensör yoğunluk alanları ile karıştırılmamalıdır. Bu mutlak tensör alanlarından biri, her zaman olduğu gibi bir ölçüm olan indislerin yükseltilmesi veya düşürülmesi ile ve ama bir küçük metrik işareti negatif bir tek sayı içeriyorsa bir diğerine dönüştürülebilir,örneğin, Minkowski uzayı için bir eksi işareti gereklidir(özel göreliliğin dört-boyutlu uzayzamanı )

${\displaystyle E^{\alpha \beta \gamma \delta }E^{\rho \sigma \mu \nu }=-g^{\alpha \zeta }g^{\beta \eta }g^{\gamma \theta }g^{\delta \iota }\delta _{\zeta \eta \theta \iota }^{\rho \sigma \mu \nu }\,}$

${\displaystyle E_{\alpha \beta \gamma \delta }E_{\rho \sigma \mu \nu }=-g_{\alpha \zeta }g_{\beta \eta }g_{\gamma \theta }g_{\delta \iota }\delta _{\rho \sigma \mu \nu }^{\zeta \eta \theta \iota }\,}$

${\displaystyle E^{\alpha \beta \gamma \delta }=-g^{\alpha \zeta }g^{\beta \eta }g^{\gamma \theta }g^{\delta \iota }E_{\zeta \eta \theta \iota }\,.}$

uyarı küçük işaretler.

Ayrıca bakınız

• Simetrik tensör
• Antisimetrik tensör
• Kronecker delta
• permutasyon konularının listesi

Kaynakça

1. P. Labelle (2010). Supersymmetry. Demystified. McGraw-Hill. s. 57–58. ISBN 978-0-07-163641-4. 
2. F. Hadrovich. "Twistor Primer". 1 Nisan 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150401000417/http://users.ox.ac.uk:80/~tweb/00004/index.shtml. Erişim tarihi: 03/09/2013. 
3. J.R. Tyldesley (1973). An introduction to Tensor Analysis: For Engineers and Applied Scientists. Longman. ISBN 0-582-44355-5. 
4. D.C. Kay (1988). Tensor Calculus. Schaum’s Outlines, McGraw Hill (USA). ISBN 0-07-033484-6. 
5. K.F. Riley, M.P. Hobson, S.J. Bence (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3. 
6. S. Lipcshutz, M. Lipson (2009). Linear Algebra (4th bas.). Schaum’s Outlines, McGraw Hill (USA). ISBN 978-0-07-154352-1. 
7. David Lovelock, Hanno Rund (1989). Tensors, Differential Forms, and Variational Principles. Courier Dover Publications. s. 113. ISBN 0-486-65840-6. 

• J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. s. p.85–86, §3.5. ISBN 0-7167-0344-0. 

Dış bağlantılar

Şablon:PlanetMath attribution

• Permutation Tensor - mathworld.wolfram

Şablon:Tensors