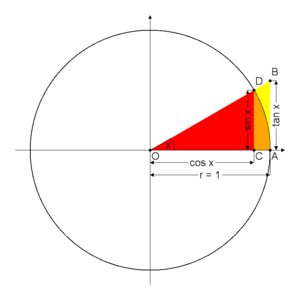Trigonometrik fonksiyonlar

Trigonometrik işlevlerin birim çember üzerinde gösterilmesi

Trigonometrik fonksiyonlar: Sinüs, Kosinüs, Tanjant, Kotanjant, Sekant, Kosekant

f(x) = sin(x) ve f(x) = cos(x) işlevlerinin kartezyen uzayında grafiksel gösterimi

Trigonometrik fonksiyonlar, matematikte bir açının işlevi olarak geçen fonksiyonlardır. Geometride üçgenleri incelerken ve periyodik olarak tekrarlanan olayları incelerken sıklıkla kullanılırlar. Genel olarak bir açısı belirli dik üçgenlerde herhangi iki kenarın oranı olarak belirtilirler, ancak birim çemberdeki belirli doğru parçalarının uzunlukları olarak da tanımlanabilirler. Daha çağdaş tanımlarda sonsuz seriler veya belirli bir türevsel denklemin çözümü olarak geçerler.

Çağdaş kullanımda, aşağıdaki tabloda da gösterildiği üzere altı tane temel trigonometrik fonksiyon vardır. Özellikle son dördünde, bu bağıntılar bu fonksiyonların tanımları olarak geçer, ama bu fonksiyonlar geometrik veya başka yollardan da tanımlanabilirler, ve bu bağıntılar o yollardan da çıkarılabilir. Bu fonksiyonlar arasındaki birçok bağıntı trigonometrik ifadeler sayfasında görülebilir.

Fonksiyon	Kısaltma	İlişki
Sinüs	sin	${\displaystyle \sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)\,}$
Kosinüs	cos	${\displaystyle \cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)\,}$
Tanjant	tan	${\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}=\cot \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\cot \theta }}\,}$
Kotanjant	cot	${\displaystyle \cot \theta ={\frac {\cos \theta }{\sin \theta }}=\tan \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\tan \theta }}\,}$
Sekant	sec	${\displaystyle \sec \theta ={\frac {1}{\cos \theta }}=\csc \left({\frac {\pi }{2}}-\theta \right)\,}$
Kosekant	csc (veya cosec)	${\displaystyle \csc \theta ={\frac {1}{\sin \theta }}=\sec \left({\frac {\pi }{2}}-\theta \right)\,}$

Sinüs ve Kosinüs fonksiyonları

1. f(x)=sin(x) işlevi dik üçgen'de Karşı dik kenar'ın Hipotenüs'e oranıdır. Koordinat Düzleminde "y" ekseni olarak tabir edilir. Bu işlevin tanım aralığı [-1,1] dir. Yani, Sinx -1 den küçük 1 den büyük olamaz.

2. f(x)=cos(x) işlevi dik üçgende Komşu dik kenar'ın Hipotenüse oranıdır. Koordinat düzleminde "x" ekseni olarak tabir edilir. Tanım aralığı f(x)=sinx işleviyle aynıdır.

Sinüs ve Kosinüs işlevleri arasında Pisagor teoreminden çıkarılabilen; Sin²x+Cos²x=1 bağıntısı vardır.

Tanjant ve Kotanjant işlevleri

3. f(x)=tanx işlevi dik üçgende Karşı dik kenar'ın Komşu dik kenara oranıdır. Koordinat Düzleminde Birim çembere "x" ekseninin pozitif tarafında teğet ve x eksenine diktir. Tanım aralığı [-∞,+∞] dır.ayrıca tanx.cotx=1 dir.

4. f(x)=cotx işlevi dik üçgende Komşu dik kenar'ın Karşı Dik kenara oranıdır. Koordinat Düzleminde Birim çembere "y" ekseninin pozitif yönünde teğet ve y eksenine diktir. Tanım aralığı [-∞,+∞] dır.

Tanjant ve Kotanjant işlevleri arasnda birim çemberde benzerlik yapılarak veya Pisagor teoreminden bulunabilen Tanx.Cotx=1 bağıntısı vardır.

Trigonometrik fonksiyonların özel değerleri

Aşağıdaki tabloda gösterildiği gibi Trigonometrik fonksiyonların bazı yaygın olarak kullanılan özel değerleri vardır,

Fonksiyon	${\displaystyle 0\ (0^{\circ })}$	${\displaystyle {\frac {\pi }{12}}\ (15^{\circ })}$	${\displaystyle {\frac {\pi }{6}}\ (30^{\circ })}$	${\displaystyle {\frac {\pi }{4}}\ (45^{\circ })}$	${\displaystyle {\frac {\pi }{3}}\ (60^{\circ })}$	${\displaystyle {\frac {5\pi }{12}}\ (75^{\circ })}$	${\displaystyle {\frac {\pi }{2}}\ (90^{\circ })}$
sin	${\displaystyle 0}$	${\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}$	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {\sqrt {2}}{2}}}$	${\displaystyle {\frac {\sqrt {3}}{2}}}$	${\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}$	${\displaystyle 1}$
cos	${\displaystyle 1}$	${\displaystyle {\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}}$	${\displaystyle {\frac {\sqrt {3}}{2}}}$	${\displaystyle {\frac {\sqrt {2}}{2}}}$	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}}$	${\displaystyle 0}$
tan	${\displaystyle 0}$	${\displaystyle 2-{\sqrt {3}}}$	${\displaystyle {\frac {\sqrt {3}}{3}}}$	${\displaystyle 1}$	${\displaystyle {\sqrt {3}}}$	${\displaystyle 2+{\sqrt {3}}}$	$\infty$[1]
cot	$\infty$[1]	${\displaystyle 2+{\sqrt {3}}}$	${\displaystyle {\sqrt {3}}}$	${\displaystyle 1}$	${\displaystyle {\frac {\sqrt {3}}{3}}}$	${\displaystyle 2-{\sqrt {3}}}$	${\displaystyle 0}$
sec	${\displaystyle 1}$	${\displaystyle {\sqrt {6}}-{\sqrt {2}}}$	${\displaystyle {\frac {2{\sqrt {3}}}{3}}}$	${\displaystyle {\sqrt {2}}}$	${\displaystyle 2}$	${\displaystyle {\sqrt {6}}+{\sqrt {2}}}$	$\infty$[1]
csc	$\infty$[1]	${\displaystyle {\sqrt {6}}+{\sqrt {2}}}$	${\displaystyle 2}$	${\displaystyle {\sqrt {2}}}$	${\displaystyle {\frac {2{\sqrt {3}}}{3}}}$	${\displaystyle {\sqrt {6}}-{\sqrt {2}}}$	${\displaystyle 1}$

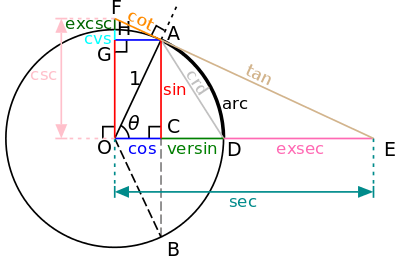
Birim çemberde tanımlar

birim çember

Bu altı trigonometrik fonksiyon birim çember'de tanımlanabilir, yarıçapı bir birim olan çemberdir. Birim çember tanımı pratik hesaplamada çok yararlar sağlar; aslında çoğu açıları için dik üçgeni kullanabiliriz.açılar 0 ve π/2 radyan'la sınırlı değildir. Birim çember bütün pozitif ve negatif açıların trigonometrik değerlerini tanımlar

Ayrıca tek bir görsel resim Aynı anda tüm önemli üçgenlerin içinde saklanmasını sağlar Pisagor teoremi'nden yararlanılarak birim çemberde şu denklemi kurabiliriz

${\displaystyle x^{2}+y^{2}=1.\,}$

Bu resim bazı yaygın açıları,negatif ve pozitif yöndeki ölçüleri, radyan ölçülerini içerir ,x-ekseninin pozitif yarısının orijinden çizilen doğru ile yaptığı açı θdır, bu birim çemberle kesişir. x- ve y-koordinatlarının bu kesim noktası ile kesiştiği nokta sırasıyla cos θ ve sin θ, değerlerine eşittir. Hipotenüs burda 1'e eşittir. böylece sin θ = y/1 ve cos θ = x/1 olacaktır

Bu değerlerin, kolay biçimde hafızaya alındığını aklınızda bulundurunuz

${\displaystyle {\frac {1}{2}}{\sqrt {0}},\quad {\frac {1}{2}}{\sqrt {1}},\quad {\frac {1}{2}}{\sqrt {2}},\quad {\frac {1}{2}}{\sqrt {3}},\quad {\frac {1}{2}}{\sqrt {4}}.}$

15°,18º,36º,54°,72º değerleri ve 75° için eldeleri aşağıdadır.

${\displaystyle \sin 15^{\circ }=\cos 75^{\circ }={\dfrac {{\sqrt {6}}-{\sqrt {2}}}{4}}\,\!}$

${\displaystyle \sin 18^{\circ }=\cos 72^{\circ }={\frac {{\sqrt {5}}-1}{4}}}$

${\displaystyle \sin 36^{\circ }=\cos 54^{\circ }={\frac {{\sqrt {10}}-2{\sqrt {5}}}{4}}}$

${\displaystyle \sin 54^{\circ }=\cos 36^{\circ }={\dfrac {{\sqrt {5}}+1}{4}}\,\!}$

${\displaystyle \sin 72^{\circ }=\cos 18^{\circ }={\frac {{\sqrt {10}}+2{\sqrt {5}}}{4}}}$

${\displaystyle \sin 75^{\circ }=\cos 15^{\circ }={\dfrac {{\sqrt {6}}+{\sqrt {2}}}{4}}\,\!}$

3º, 6º, 9º, 81º, 84º, ve 87º için değerleri analitik olarak hesaplanabilr.

${\displaystyle \sin 3^{\circ }=\cos 87^{\circ }={\dfrac {{\sqrt {30}}+{\sqrt {10}}+{\sqrt {20+4{\sqrt {5}}}}-{\sqrt {6}}-{\sqrt {2}}-{\sqrt {60+12{\sqrt {5}}}}}{16}}\,\!}$

${\displaystyle \sin 6^{\circ }=\cos 84^{\circ }={\dfrac {{\sqrt {30-6{\sqrt {5}}}}-{\sqrt {5}}-1}{8}}\,\!}$

${\displaystyle \sin 9^{\circ }=\cos 81^{\circ }={\dfrac {{\sqrt {90}}+{\sqrt {18}}+{\sqrt {10}}+{\sqrt {2}}-{\sqrt {20-4{\sqrt {5}}}}-{\sqrt {180-36{\sqrt {5}}}}}{32}}\,\!}$

${\displaystyle \sin 84^{\circ }=\cos 6^{\circ }={\frac {{\sqrt {10}}-2{\sqrt {5}}+{\sqrt {15}}+{\sqrt {3}}}{8}}}$

${\displaystyle \sin 87^{\circ }=\cos 3^{\circ }={\frac {{\sqrt {60+12{\sqrt {5}}}}+{\sqrt {20+4{\sqrt {5}}}}+{\sqrt {30}}+{\sqrt {2}}-{\sqrt {6}}-{\sqrt {10}}}{16}}}$

Sinüs ve kosinüs fonksiyonları Kartezyen düzlemde grafikle gösterilebilir.

2π ve daha büyük açılar için az-2π ve daha küçük açılar için çember etrafında sadece bir daire etrafında dönmeye devam ederler

sin ve cos periyodik fonksiyon ve periodu 2π'dir

${\displaystyle \sin \theta =\sin \left(\theta +2\pi k\right),\,}$

${\displaystyle \cos \theta =\cos \left(\theta +2\pi k\right),\,}$

herhangi bir açı θ ve herhangi bir tamsayı  k 'dır.

Seri tanımları

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full cycle centered on the origin.

Trigonometrik fonksiyonların Taylor serisi'ne açılımları aşağıdaki gibidir. bütün x:^[2] gerçek sayılar için

${\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},\\\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}}$

Bu iki serinin şu toplamı Euler formülü'nü verir: cos x + i sin x = e^ix. Diğer serilerde bulunabilir.^[3] Aşağıdaki trigonometrik fonksiyonlar için:

U_n ninci üst/alt sayı'dır,

B_n ninci Bernoulli sayısı'dır, ve

E_n (aşağıda) ninci Euler sayısı'dır.

Tanjant

${\displaystyle {\begin{aligned}\tan x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\\&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}.\end{aligned}}}$

Eğer seri tanjant fonksiyonu ilgili faktöriyelleri ile ifade edilecekse,kombinatorik yorumlamada,kardinal teksayıların sonlu sayıda permutasyon alternatifleri vardır bunlar "tanjant sayıları" olarak adlandırılır .^[4]

Kosekant

${\displaystyle {\begin{aligned}\csc x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}$

Secant

${\displaystyle {\begin{aligned}\sec x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\\&{}=1+{\frac {1}{2}}x^{2}+{\frac {5}{24}}x^{4}+{\frac {61}{720}}x^{6}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}.\end{aligned}}}$

Eğer seri sekant fonksiyonu ilgili faktöriyelleri ile ifade edilecekse,kombinatorik yorumlamada, kardinal teksayıların sonlu sayıda permutasyon alternatifleri vardır bunlar "sekant sayıları" olarak adlandırılır .^[4]

Kotanjant

${\displaystyle {\begin{aligned}\cot x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{for }}0<|x|<\pi .\end{aligned}}}$

kotanjant fonksiyonu ve ters fonksiyonlar için:^[5]

${\displaystyle \pi \cdot \cot(\pi x)=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{x+n}}.}$

Bu eşitlik Herglotz hilesi ile ispat edilir.^[6] ${\displaystyle -n}$-inci ve ${\displaystyle n}$-inci terimleri birleştirilerek mutlak yakınsak seri:

${\displaystyle \pi \cdot \cot(\pi x)={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2x}{x^{2}-n^{2}}}.}$

Üstel fonksiyonlar ve karmaşık sayılarla İlişkisi

Euler formulünün üç boyutlu heliksle gösterimi, birim çemberin 2-D ortogonal parçası ile başlıyor, sin ve cos (θ yerine = t ).

${\displaystyle e^{i\theta }=\cos \theta +i\sin \theta .\,}$

Bu eşitlik Euler formülüdür. Karmaşık analizin geometrik yorumlanmasının esasını oluşturur. Örnek olarak Karmaşık düzlem'de birim çemberin e ^ix, parametrizasyonu gibi. Burdaki paramatreler cos ve sin'dir. Euler formülü ile aşağıdaki sin ve cos trigonometrik eşitlikler yazılabilir:

${\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\;}$

${\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\;}$

Dahası,trigonometrik fonksiyonların bu karmaşık argümanları için z tanımını sağlar :

${\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}={\frac {e^{iz}-e^{-iz}}{2i}}\,={\frac {\sinh \left(iz\right)}{i}}}$

${\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}={\frac {e^{iz}+e^{-iz}}{2}}\,=\cosh \left(iz\right)}$

burada i ² = −1. sine ve cos tam fonksiyon'dur. Ayrıca, x saf gerçeldir,

${\displaystyle \cos x=\operatorname {Re} (e^{ix})\,}$

${\displaystyle \sin x=\operatorname {Im} (e^{ix})\,}$

Ayrıca argümanları gerçek ve sanal kısımları bakımından karmaşık sinüs ve kosinüs fonksiyonları ifade etmek bazen yararlıdır.

${\displaystyle \sin(x+iy)=\sin x\cosh y+i\cos x\sinh y,\,}$

${\displaystyle \cos(x+iy)=\cos x\cosh y-i\sin x\sinh y.\,}$

Bu (sin, cos) fonksiyonlarından yararlanılarak hiperbolik gerçek (sinh, cosh) karşılıkları bulunabilir.

Karmaşık grafik

Aralık değerinin parlaklığın büyüklüğü (mutlak değeri) gösterir. Parlaklığı siyah olan değer sıfırdır. Renk tonu pozitif reel eksenle ölçülen, argüman veya açı ile değişir.(more)

Ayrıca bakınız

• Trigonometrik tabloların Üretimi
• Aryabhata sinüs tablosu
• Madhava sinüs tablosu
• Madhava serisi
• Bhaskara sinüs yaklaşıklığı formülü
• Hiperbolik fonksiyon
• Birim vektör(cos yön açıklaması)
• Newton serisi tablosu
• Trigonometrik eşitliklerin listesi
• Trigonometrik eşitliklerin kanıtları
• Euler formülü
• Polar sinüs—köşe açıları bir genellemesi
• Gauss sürekli kesri —tanjant fonksiyonu tanımı için bir sürekli kesir
• Genelleştirilmiş trigonometri

Notlar

1. Abramowitz, Milton and Irene A. Stegun, p.74
2. See Ahlfors, pages 43–44.
3. Abramowitz; Weisstein.
4. Stanley, Enumerative Combinatorics, Vol I., page 149
5. Aigner, Martin; Ziegler, Günter M. (2000). Proofs from THE BOOK (Second bas.). Springer-Verlag. s. 149. ISBN [[Special:BookSources/9773540678657 Şablon:Please check ISBN|9773540678657 Şablon:Please check ISBN]]. http://www.springer.com/mathematics/book/978-3-642-00855-9. 
6. Remmert, Reinhold (1991). Theory of complex functions. Springer. s. 327. ISBN 0-387-97195-5. http://books.google.com/books?id=CC0dQxtYb6kC. , Extract of page 327

Kaynakça

• Abramowitz, Milton and Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, New York. (1964). ISBN 0-486-61272-4.
• Lars Ahlfors, Complex Analysis: an introduction to the theory of analytic functions of one complex variable, second edition, McGraw-Hill Book Company, New York, 1966.
• Boyer, Carl B., A History of Mathematics, John Wiley & Sons, Inc., 2nd edition. (1991). ISBN 0-471-54397-7.
• Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transaction on Mathematical Software (1991).
• Joseph, George G., The Crest of the Peacock: Non-European Roots of Mathematics, 2nd ed. Penguin Books, London. (2000). ISBN 0-691-00659-8.
• Kantabutra, Vitit, "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
• Maor, Eli, Trigonometric Delights, Princeton Univ. Press. (1998). Reprint edition (February 25, 2002): ISBN 0-691-09541-8.
• Needham, Tristan, "Preface"" to Visual Complex Analysis. Oxford University Press, (1999). ISBN 0-19-853446-9.
• O'Connor, J.J., and E.F. Robertson, "Trigonometric functions", MacTutor History of Mathematics archive. (1996).
• O'Connor, J.J., and E.F. Robertson, "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2000).
• Pearce, Ian G., "Madhava of Sangamagramma", MacTutor History of Mathematics archive. (2002).
• Weisstein, Eric W., "Tangent" from MathWorld, accessed 21 January 2006.

Dış bağlantılar

Vikikitapta bu konu hakkında daha fazla bilgi var:

Trigonometry

• Visionlearning Module on Wave Mathematics
• GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions
• Dave's draggable diagram. (Requires java browser plugin)