Trigonometrik integral

Si(x) (mavi) ve Ci(x) (yeşil) çizim olarak aynı düzlemde.

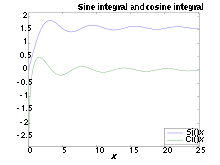
Matematikte, trigonometrik integral trigonometrik fonksiyonların integralinin bir ailesini içerir. temel trigonometrik integralin bir sayısı trigonometrik fonksiyonların integralinin bir listesi dersindedir.

Sine integral

Si(x) için 0 ≤ x ≤ 8π.nin grafiği

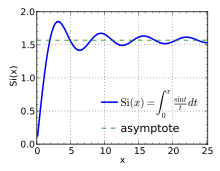
farklı bir sin integrali tanımıdır:

${\displaystyle {\rm {Si}}(x)=\int _{0}^{x}{\frac {\sin t}{t}}\,dt}$

${\displaystyle {\rm {si}}(x)=-\int _{x}^{\infty }{\frac {\sin t}{t}}\,dt}$

Böylece tanım ile, ${\displaystyle {\rm {Si}}(x)}$ ifadesi ${\displaystyle \sin x/x}$'nin ilkeli ${\displaystyle x=0}$ için sıfırdır ve ${\displaystyle {\rm {si}}(x)}$ ifadesi ${\displaystyle \sin x/x}$ ilkeli bu ${\displaystyle x=\infty }$ için sıfırdır.İlişki ile verilen

${\displaystyle {\rm {Si}}(x)-{\rm {si}}(x)=\int _{0}^{\infty }{\frac {\sin t}{t}}\,dt={\frac {\pi }{2}},}$

burada son integral Dirichlet integrali olarak bilinir. Unutmadan ${\displaystyle {\frac {\sin t}{t}}}$ sinc fonksiyonu ve ayrıca sıfırıncı küresel Bessel fonksiyonudur.

işaret işlemede,Sine integralin salınımı ileri taşıma nedeniyle ve parazit fazlalıklar ise sinc filtresi kullanılıyor, ve frekans domeni gürültüsü olarak bir alçak-geçiren filtre olarak eğer bir sinc filtresi gövdesi kullanılıyor .

Gibbs fenomeni bir ilişkili fenomendir:sinc olarak bir alçak-geçiren filtrenin düşüncesi ve Sine integral olarak Heaviside basamak fonksiyonu ile, bu evrişimdir . Gibbs fenomeni nedeniyle Fourier serisinin gövdesine karşılıktır

Cosine integral

Ci(x) için 0 < x ≤ 8π.nin çizimi

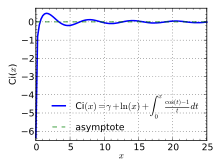
farklı cos integral tanımı :

${\displaystyle {\rm {Ci}}(x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cos t-1}{t}}\,dt}$

${\displaystyle {\rm {ci}}(x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt}$

${\displaystyle {\rm {Cin}}(x)=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt}$

burada ${\displaystyle \gamma }$ Euler–Mascheroni sabitidir.

${\displaystyle {\rm {ci}}(x)}$ ifadesi ${\displaystyle \cos x/x}$ ifadesi ${\displaystyle x=\infty }$ in sıfır için ilkelidir. elimizde:

${\displaystyle {\rm {ci}}(x)={\rm {Ci}}(x)\,}$

${\displaystyle {\rm {Cin}}(x)=\gamma +\ln x-{\rm {Ci}}(x)\,}$

Hiperbolik sine integral

hiperbolik sine integral:

${\displaystyle {\rm {Shi}}(x)=\int _{0}^{x}{\frac {\sinh t}{t}}\,dt={\rm {shi}}(x).}$

${\displaystyle {\rm {Shi}}(x)=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)^{2}(2n)!}}=x+{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}+{\frac {x^{7}}{7!\cdot 7}}+\cdots .}$

Hiperbolik cosine integral

The hiperbolik cosine integral

${\displaystyle {\rm {Chi}}(x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt={\rm {chi}}(x)}$

Nielsen'in spirali

Nielsen'in spirali.

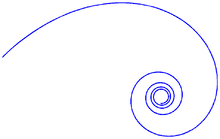
spiral formu si,ci'nin parametrik grafik tarafından Nielsen'in spiral olarak bilinir.Ayrıca o Euler spirali olarak ifade edilir, the Cornu spiral, bir klotoid, veya polinomal spiral bir-eğri olarak.spiral is ayrıca Fresnel integraliyle yakından ilişkilidir. Bu spiral görsel işleme içinde uygulamalarda ,yol ve pist yapımı ve diğer alanlarda var.

Açılım

Çeşitli açılımlar argüman aralığına bağlı olarak, Trigonometrik integraller değerlendirilmesi için kullanılabilir.

Asimptotik seriler (büyük bileşen için)

${\displaystyle {\rm {Si}}(x)={\frac {\pi }{2}}-{\frac {\cos x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\sin x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)}$

${\displaystyle {\rm {Ci}}(x)={\frac {\sin x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\cos x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)}$

Bu seri asimptotik ve ıraksaktır, hatta hassas değerlendirme tahminleri için kullanılan ve olmasına rağmen ${\displaystyle ~{\rm {Re}}(x)\gg 1~}$ olur.

yakınsak seriler

${\displaystyle {\rm {Si}}(x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}\pm \cdots }$

${\displaystyle {\rm {Ci}}(x)=\gamma +\ln x+\sum _{n=1}^{\infty }{\frac {(-1)^{n}x^{2n}}{2n(2n)!}}=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}\mp \cdots }$

Bu seriler herhangi karmaşık ${\displaystyle ~x~}$ için yakınsaktır, ${\displaystyle |x|\gg 1}$ için sınırlı yavaş yakınsak seriler olmasına rağmen, henüz kesinleşmediği için birçok terimler gerektiren.

Sanal bileşenin üstel integrali ile ilişkisi

Bu fonksiyon

${\displaystyle {\rm {E}}_{1}(z)=\int _{1}^{\infty }{\frac {\exp(-zt)}{t}}\,{\rm {d}}t\qquad ({\rm {Re}}(z)\geq 0)}$

üstel integral denir. Bu Si ve Ci ye yakın ilişkilidir:

${\displaystyle {\rm {E}}_{1}({\rm {i}}\!~x)=i\left(-{\frac {\pi }{2}}+{\rm {Si}}(x)\right)-{\rm {Ci}}(x)=i~{\rm {si}}(x)-{\rm {ci}}(x)\qquad (x>0)}$

Her ilgili fonksiyon bileşenin negatif değerlerde kesilmiş analitik hariç olarak,ilişkinin geçerlilik alanı genişletilmiş olmalıdır ${\displaystyle {\rm {Re}}(x)>0}$. ( bu sınırın dışı,bu toplanabilir terimlerin $\pi$ nin tamsayı çarpanları ifadededir).

Genelleştirilmiş integro-üstel fonksiyonun sanal argüman durumlar aşağıdadır

${\displaystyle \int _{1}^{\infty }\cos(ax){\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}+\sum _{n\geq 1}{\frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}},}$

reel parçası olan

${\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}-{\frac {\pi }{2}}i(\gamma +\ln a)+\sum _{n\geq 1}{\frac {(ia)^{n}}{n!n^{2}}}.}$

Similarly

${\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}dx=1+ia[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1-{\frac {i\pi }{2}}(\gamma +\ln a-1)]+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}.}$

Verimli değerlendirme

Padé yaklaşıklığı yakınsak Taylor serisi küçük bağımsız değişkenler için fonksiyonların değerlendirilmesi için etkili bir yol sağlar. Aşağıdaki formüller için ${\displaystyle 0\leq x\leq 4}$ için ${\displaystyle 10^{-16}}$ den daha doğrudur:

${\displaystyle {\begin{array}{rcl}{\rm {Si}}(x)&=&x\cdot \left({\frac {\begin{array}{l}1-4.54393409816329991\cdot 10^{-2}\cdot x^{2}+1.15457225751016682\cdot 10^{-3}\cdot x^{4}-1.41018536821330254\cdot 10^{-5}\cdot x^{6}\\~~~+9.43280809438713025\cdot 10^{-8}\cdot x^{8}-3.53201978997168357\cdot 10^{-10}\cdot x^{10}+7.08240282274875911\cdot 10^{-13}\cdot x^{12}\\~~~-6.05338212010422477\cdot 10^{-16}\cdot x^{14}\end{array}}{\begin{array}{l}1+1.01162145739225565\cdot 10^{-2}\cdot x^{2}+4.99175116169755106\cdot 10^{-5}\cdot x^{4}+1.55654986308745614\cdot 10^{-7}\cdot x^{6}\\~~~+3.28067571055789734\cdot 10^{-10}\cdot x^{8}+4.5049097575386581\cdot 10^{-13}\cdot x^{10}+3.21107051193712168\cdot 10^{-16}\cdot x^{12}\end{array}}}\right)\\&~&\\{\rm {Ci}}(x)&=&\gamma +\ln(x)+\\&&x^{2}\cdot \left({\frac {\begin{array}{l}-0.25+7.51851524438898291\cdot 10^{-3}\cdot x^{2}-1.27528342240267686\cdot 10^{-4}\cdot x^{4}+1.05297363846239184\cdot 10^{-6}\cdot x^{6}\\~~~-4.68889508144848019\cdot 10^{-9}\cdot x^{8}+1.06480802891189243\cdot 10^{-11}\cdot x^{10}-9.93728488857585407\cdot 10^{-15}\cdot x^{12}\\\end{array}}{\begin{array}{l}1+1.1592605689110735\cdot 10^{-2}\cdot x^{2}+6.72126800814254432\cdot 10^{-5}\cdot x^{4}+2.55533277086129636\cdot 10^{-7}\cdot x^{6}\\~~~+6.97071295760958946\cdot 10^{-10}\cdot x^{8}+1.38536352772778619\cdot 10^{-12}\cdot x^{10}+1.89106054713059759\cdot 10^{-15}\cdot x^{12}\\~~~+1.39759616731376855\cdot 10^{-18}\cdot x^{14}\\\end{array}}}\right)\end{array}}}$

${\displaystyle x>4}$ için,yardımcı fonksiyonlar kullanılabilir:

${\displaystyle {\begin{array}{rcl}f(x)&=&\int _{0}^{\infty }{\frac {sin(t)}{t+x}}dt=\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}dt~=~{\rm {Ci}}(x)\sin(x)+\left({\frac {\pi }{2}}-{\rm {Si}}(x)\right)\cos(x)\\g(x)&=&\int _{0}^{\infty }{\frac {cos(t)}{t+x}}dt=\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}dt~=~-{\rm {Ci}}(x)\cos(x)+\left({\frac {\pi }{2}}-{\rm {Si}}(x)\right)\sin(x)\\\end{array}}}$

bu kullanılıyor,trigonometrik integraller belki şöyle gösterilebilir

${\displaystyle {\begin{array}{rcl}{\rm {Si}}(x)&=&{\frac {\pi }{2}}-f(x)\cos(x)-g(x)\sin(x)\\{\rm {Ci}}(x)&=&f(x)\sin(x)-g(x)\cos(x)\\\end{array}}}$

${\displaystyle \;\;{\frac {1}{\sqrt {y}}}\;f\left({\frac {1}{\sqrt {y}}}\right)\;\;}$ ve ${\displaystyle \;\;{\frac {1}{y}}\;g\left({\frac {1}{\sqrt {y}}}\right)\;\;}$ nin Chebyshev-Padé açılımları ${\displaystyle 0..{\frac {1}{4^{2}}}}$ aralığı yaklaşıklığı aşağıda verilmiştir, ${\displaystyle x\geq 4}$:için ${\displaystyle 10^{-16}}$ dan daha iyidir

${\displaystyle {\begin{array}{rcl}f(x)&=&{\dfrac {1}{x}}\cdot \left({\frac {\begin{array}{l}1+7.44437068161936700618\cdot 10^{2}\cdot x^{-2}+1.96396372895146869801\cdot 10^{5}\cdot x^{-4}+2.37750310125431834034\cdot 10^{7}\cdot x^{-6}\\~~~+1.43073403821274636888\cdot 10^{9}\cdot x^{-8}+4.33736238870432522765\cdot 10^{10}\cdot x^{-10}+6.40533830574022022911\cdot 10^{11}\cdot x^{-12}\\~~~+4.20968180571076940208\cdot 10^{12}\cdot x^{-14}+1.00795182980368574617\cdot 10^{13}\cdot x^{-16}+4.94816688199951963482\cdot 10^{12}\cdot x^{-18}\\~~~-4.94701168645415959931\cdot 10^{11}\cdot x^{-20}\end{array}}{\begin{array}{l}1+7.46437068161927678031\cdot 10^{2}\cdot x^{-2}+1.97865247031583951450\cdot 10^{5}\cdot x^{-4}+2.41535670165126845144\cdot 10^{7}\cdot x^{-6}\\~~~+1.47478952192985464958\cdot 10^{9}\cdot x^{-8}+4.58595115847765779830\cdot 10^{10}\cdot x^{-10}+7.08501308149515401563\cdot 10^{11}\cdot x^{-12}\\~~~+5.06084464593475076774\cdot 10^{12}\cdot x^{-14}+1.43468549171581016479\cdot 10^{13}\cdot x^{-16}+1.11535493509914254097\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\&&\\g(x)&=&{\dfrac {1}{x^{2}}}\cdot \left({\frac {\begin{array}{l}1+8.1359520115168615\cdot 10^{2}\cdot x^{-2}+2.35239181626478200\cdot 10^{5}\cdot x^{-4}+3.12557570795778731\cdot 10^{7}\cdot x^{-6}\\~~~+2.06297595146763354\cdot 10^{9}\cdot x^{-8}+6.83052205423625007\cdot 10^{10}\cdot x^{-10}+1.09049528450362786\cdot 10^{12}\cdot x^{-12}\\~~~+7.57664583257834349\cdot 10^{12}\cdot x^{-14}+1.81004487464664575\cdot 10^{13}\cdot x^{-16}+6.43291613143049485\cdot 10^{12}\cdot x^{-18}\\~~~-1.36517137670871689\cdot 10^{12}\cdot x^{-20}\end{array}}{\begin{array}{l}1+8.19595201151451564\cdot 10^{2}\cdot x^{-2}+2.40036752835578777\cdot 10^{5}\cdot x^{-4}+3.26026661647090822\cdot 10^{7}\cdot x^{-6}\\~~~+2.23355543278099360\cdot 10^{9}\cdot x^{-8}+7.87465017341829930\cdot 10^{10}\cdot x^{-10}+1.39866710696414565\cdot 10^{12}\cdot x^{-12}\\~~~+1.17164723371736605\cdot 10^{13}\cdot x^{-14}+4.01839087307656620\cdot 10^{13}\cdot x^{-16}+3.99653257887490811\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\\end{array}}}$

Burada yukardaki için uygun bilgisayar kod girişi bölüm versiyonları kopyalıdır( x2 = x*x ve y = 1/(x*x) burada yaklaşıklık kullanılıyor):

   Si = x*(1. +
           x2*(-4.54393409816329991e-2 +
               x2*(1.15457225751016682e-3 +
                   x2*(-1.41018536821330254e-5 +
                       x2*(9.43280809438713025e-8 +
                           x2*(-3.53201978997168357e-10 +
                               x2*(7.08240282274875911e-13 +
                                   x2*(-6.05338212010422477e-16))))))))
        / (1. + 
           x2*(1.01162145739225565e-2 +
               x2*(4.99175116169755106e-5 + 
                   x2*(1.55654986308745614e-7 +
                       x2*(3.28067571055789734e-10 +
                           x2*(4.5049097575386581e-13 + 
                               x2*(3.21107051193712168e-16)))))))
   
   Ci = 0.577215664901532861 + ln(x) + 
        x2*(-0.25 +
            x2*(7.51851524438898291e-3 +
                x2*(-1.27528342240267686e-4 + 
                    x2*(1.05297363846239184e-6 +
                        x2*(-4.68889508144848019e-9 +
                            x2*(1.06480802891189243e-11 +
                                x2*(-9.93728488857585407e-15)))))))
        / (1. +
           x2*(1.1592605689110735e-2 +
               x2*(6.72126800814254432e-5 + 
                   x2*(2.55533277086129636e-7 +
                       x2*(6.97071295760958946e-10 +
                           x2*(1.38536352772778619e-12 + 
                               x2*(1.89106054713059759e-15 +
                                   x2*(1.39759616731376855e-18))))))))
   
   f = (1. + 
        y*(7.44437068161936700618e2 +
           y*(1.96396372895146869801e5 +
              y*(2.37750310125431834034e7 +
                 y*(1.43073403821274636888e9 +
                    y*(4.33736238870432522765e10 +
                       y*(6.40533830574022022911e11 +
                          y*(4.20968180571076940208e12 +
                             y*(1.00795182980368574617e13 +
                                y*(4.94816688199951963482e12 +
                                   y*(-4.94701168645415959931e11)))))))))))                                                               
        / (x*(1. +
              y*(7.46437068161927678031e2 +
                 y*(1.97865247031583951450e5 +
                    y*(2.41535670165126845144e7 +
                       y*(1.47478952192985464958e9 +
                          y*(4.58595115847765779830e10 +
                             y*(7.08501308149515401563e11 +
                                y*(5.06084464593475076774e12 +
                                   y*(1.43468549171581016479e13 +
                                      y*(1.11535493509914254097e13)))))))))))
   
   g = y*(1. +
          y*(8.1359520115168615e2 +
             y*(2.35239181626478200e5 +
                y*(3.12557570795778731e7 +
                   y*(2.06297595146763354e9 +
                      y*(6.83052205423625007e10 +
                         y*(1.09049528450362786e12 +
                            y*(7.57664583257834349e12 +
                               y*(1.81004487464664575e13 +
                                  y*(6.43291613143049485e12 +
                                     y*(-1.36517137670871689e12)))))))))))
       / (1. +
          y*(8.19595201151451564e2 +
             y*(2.40036752835578777e5 +
                y*(3.26026661647090822e7 +
                   y*(2.23355543278099360e9 +
                      y*(7.87465017341829930e10 +
                         y*(1.39866710696414565e12 +
                            y*(1.17164723371736605e13 +
                               y*(4.01839087307656620e13 +
                                  y*(3.99653257887490811e13))))))))))

Ayrıca bakınız

• Matematiksel fonksiyonların listesi
• Üstel integral
• Logaritmik(altal) integral

Sinyal işleme

• Gibbs fenomeni
• Zil anomalisi

Kaynakça

• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.8.2. Cosine and Sine Integrals", Numerical Recipes: The Art of Scientific Computing (3rd bas.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=300 
• Şablon:Dlmf
• Mathar, R. J. (2009). "Numerical evaluation of the oscillatory integral over exp(iπx)·x^1/x between 1 and ∞". arΧiv: 0912.3844. , Appendix B.
• Sine Integral Taylor series proof.

Dış bağlantılar

• http://mathworld.wolfram.com/SineIntegral.html
• Hazewinkel, Michiel, ed. (2001), "Integral sine", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/p/i051650.htm 
• Hazewinkel, Michiel, ed. (2001), "Integral cosine", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104, http://eom.springer.de/p/i051370.htm