Galile dönüşümü

Fizikte, bir Galile dönüşümü Newton fiziğinin yapıları içinde sürekli bağıl hareket ile sadece farklı iki referans çerçevesi koordinatlarını arasındaki dönüşüm için kullanılır. Bu bakış pasif dönüşüm noktasıdır. Aşağıdaki denklemler, görünüşe göre belirgin olmasına rağmen,ışık hızı'na yaklaştığınız hızlarda savunulamaz hale gelir.Özel görelilik'te olarak Galile dönüşümleri Lorentz dönüşümü olarak değiştirilir Galileo düzgün hareket ^[1] için yaptığı açıklama ile bu kavramlar formüle edilmiştir,konu bir rampa'dan aşağı yuvarlanan bir topun hareketi Galileo'nun açıklamasına göre ilham oldu, hangi o Dünya'nın yüzeyine yakın yerçekimi ivmesi için sayısal değeri ile ölçülebilir . Mutlak zaman ve mekan Isaac Newton tarafından tasarlanmis ve Galileo dönüşümleri adını almasına rağmen, bu tanım kendi etki alanıni sağlar. Özünde, Galile dönüşümleri hızların vektörler olarak toplama ve çıkarma sezgisel kavramlarını somutlaştırmak içindir.

Öteleme

Galile dönüşümleri için koordinat sistemlerini standart yapılandırma.

Dönüşümler Galileo adını almasına rağmen,Isaac Newton tarafından sağlanan bu tanım özünde mutlak uzay mutlak zaman etki alanı sağlar,Galile dönüşümlerini vektörler olarak hızların toplama ve çıkarmasının sezgisel gösterimini somutlastirir ve adina mutlak uzay-zaman denir Bu varsayımda,Galilean dönüşümü Lorentz dönüşümü için bir düşük hız yaklaşımi olarak kabul edilebilir iken göreceli dönüşümler tüm hızlar için geçerli Lorentz dönüşümlerine terk edilir.

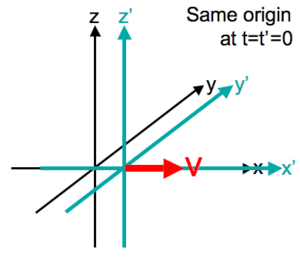
Aşağıdaki notasyon,koordinatlar arasında Galileo dönüşümü altındaki ilişkiyi açıklar (x,y,z,t) ve (x′,y′,z′,t′) tek bir rastgele olay olarak iki koordinat sistemi S and S' ölçülür 'mekansal kökenleri zaman t=t'=0 denk olan yön,' ortak x ve x’ tek tip bağıl hareket (hız v) dir: ^{[2] [3] [4] [5]}

${\displaystyle x'=x-vt\,}$

${\displaystyle y'=y\,}$

${\displaystyle z'=z\,}$

${\displaystyle t'=t\,}$

Son denklem farklı gözlemciler için göreli hareket bağımsız mutlak uzayzaman varsayımıni ifade etmektedir

Lineer cebir dilinde, bu dönüşüm bir kesme haritalama olarak kabul edilir ve bu hareket eden vektör bir matris ile açıklanmıştır. x eksenine paralel bir hareket ile, dönüşüm sadece iki bileşen üzerinde hareket eder.Matris temsilleri Galile dönüşümü için kesinlikle gerekli olmamakla birlikte, özel görelilik dönüşüm yöntemleri için doğrudan karşılaştırmaya bir yol sağlar

${\displaystyle (x',t')=(x,t){\begin{pmatrix}1&0\\-v&1\end{pmatrix}}.}$

Galile dönüşümleri

Hızlanan bir gözlemcinin dünya çizgisi boyunca uzay manzarası.

Galile'n simetrisi uzay zamanın bir dönüşü, bir öteleme ve bir yalin hareketinin düzeni yalin olarak yazılabilir .^[6] Diyelimki x üç-boyutlu uzay içinde bir nokta gösterim ve t tek-boyutlu zamanda bir nokta gösterimidir.Uzay-zaman içinde verilen bir genel nokta sırasıyla (x,t) çifti tarafından verilir. Bu yalin gösterim,v hızı ile, şöyle verilir ${\displaystyle ({\mathbf {x}},t)\mapsto ({\mathbf {x}}+t{\mathbf {v}},t)}$ burada v R³ içindedir. Bu ${\displaystyle ({\mathbf {x}},t)\mapsto ({\mathbf {x}}+{\mathbf {a}},t+b)}$ tarafından ötelenerek verilir. burada a R³ içindedir ve b R içindedir. Bir dönüş ${\displaystyle ({\mathbf {x}},t)\mapsto (G{\mathbf {x}},t)}$ olarak verilir burada G : R³ → R³ bir ortogonal dönüşümdür.^[6] bir Lie grubu olarak, Galilean dönüşümlerinin 10 boyutu var.^[6]

Galile gruplarının merkezi uzantıları

Galile grupları: Burada, biz sadece Lie cebri'ne bakacağız.Bu sonuçları Lie grup'larına genişletmek kolaydır.L'nin Lie cebri H, P_i, C_i ve L_ij (antisimetrik tensör) tarafından yayılmış değişmeli'lerdir,bunlar

${\displaystyle [H,P_{i}]=0\,\!}$

${\displaystyle [P_{i},P_{j}]=0\,\!}$

${\displaystyle [L_{ij},H]=0\,\!}$

${\displaystyle [C_{i},C_{j}]=0\,\!}$

${\displaystyle [L_{ij},L_{kl}]=i[\delta _{ik}L_{jl}-\delta _{il}L_{jk}-\delta _{jk}L_{il}+\delta _{jl}L_{ik}]\,\!}$

${\displaystyle [L_{ij},P_{k}]=i[\delta _{ik}P_{j}-\delta _{jk}P_{i}]\,\!}$

${\displaystyle [L_{ij},C_{k}]=i[\delta _{ik}C_{j}-\delta _{jk}C_{i}]\,\!}$

${\displaystyle [C_{i},H]=iP_{i}\,\!}$

${\displaystyle [C_{i},P_{j}]=0\,\!.}$

(Hamiltoniyen)zaman çevriminin üreteci H'dır,(momentum operatör) çevriminin üreteci P_itir, Galile boost'unun üreteci C_i dir ve (açısal momentum operatörü) dönmesinin genel bir durumu için L_ij'dir.

Bir merkez uzantıları'nı şimdi verebiliriz. H', P'_i, tarafından yayılmış Lie cebri içinde C'_i, L'_ij (antisimetrik tensör)dür, M böylece M değişimi ile her şey değişir (yani merkez içinde yatık, bu yüzden buna merkezi bir uzantısı denir ) ve

${\displaystyle [H',P'_{i}]=0\,\!}$

${\displaystyle [P'_{i},P'_{j}]=0\,\!}$

${\displaystyle [L'_{ij},H']=0\,\!}$

${\displaystyle [C'_{i},C'_{j}]=0\,\!}$

${\displaystyle [L'_{ij},L'_{kl}]=i[\delta _{ik}L'_{jl}-\delta _{il}L'_{jk}-\delta _{jk}L'_{il}+\delta _{jl}L'_{ik}]\,\!}$

${\displaystyle [L'_{ij},P'_{k}]=i[\delta _{ik}P'_{j}-\delta _{jk}P'_{i}]\,\!}$

${\displaystyle [L'_{ij},C'_{k}]=i[\delta _{ik}C'_{j}-\delta _{jk}C'_{i}]\,\!}$

${\displaystyle [C'_{i},H']=iP'_{i}\,\!}$

${\displaystyle [C'_{i},P'_{j}]=iM\delta _{ij}\,\!}$

Ayrıca bakınız

• Galile grubun Temsil teorisi
• Lorentz grubu
• Poincaré grubu
• Lagrange ve Euler koordinatları

Notlar

1. Galileo 1638 Discorsi e Dimostrazioni Matematiche, intorno á due nuoue scienze 191 - 196, published by Lowys Elzevir (Louis Elsevier), Leiden, or Two New Sciences, English translation by Henry Crew and Alfonso de Salvio 1914, reprinted on pages 515-520 of On the Shoulders of Giants: The Great Works of Physics and Astronomy. Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
2. Mould, Richard A. (2002), Basic relativity, Springer-Verla, ISBN 0-387-95210-1, http://books.google.com/?id=lfGE-wyJYIUC&pg=PA42 , Chapter 2 §2.6, p. 42
3. Lerner, Lawrence S. (1996), Physics for Scientists and Engineers, Volume 2, Jones and Bertlett Publishers, Inc, ISBN 0-7637-0460-1, http://books.google.com/?id=B8K_ym9rS6UC&pg=PA1047 , Chapter 38 §38.2, p. 1046,1047
4. Serway, Raymond A.; Jewett, John W. (2006), Principles of Physics: A Calculus-based Text, Fourth Edition, Brooks/Cole - Thomson Learning, ISBN 0-534-49143-X, http://books.google.com/?id=1DZz341Pp50C&pg=PA261 , Chapter 9 §9.1, p. 261
5. Hoffmann, Banesh (1983), Relativity and Its Roots, Scientific American Books, ISBN 0-486-40676-8, http://books.google.com/?id=JokgnS1JtmMC&pg=PA83 , Chapter 5, p. 83
6. Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics (2 bas.). Springer-Verlag. s. 6. ISBN 0-387-96890-3. http://www.springer.com/mathematics/analysis/book/978-0-387-96890-2. 

Şablon:Galileo Galilei Şablon:Relativity