Sabit fonksiyon

Fonksiyon

x \mapsto f (x)

tanım ve değer kümesine göre

$X$	—›	$B$			$B n$	—›	$B$
$X$	—›	$Z$	—›	$X$
$X$	—›	$R$	—›	$X$	$R n$	—›	$X$
$X$	—›	$C$	—›	$X$	$C n$	—›	$X$

Sınıflar/özellikler

Sabit · Birim · Doğrusal · Polinom · Rasyonel · Cebirsel · Analitik · Yumuşak · Sürekli · Ölçülebilir · Birebir · Örten · Birebir örten

Yapılar

Kısıtlama · Bileşim · λ · Terslik

Genellemeler

Parçalı · Çokdeğerli · Kapalı

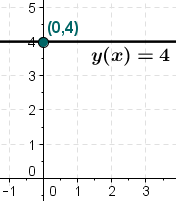
Sabit fonksiyon: y=4

Matematikte sabit fonksiyon, her giriş değeri için çıkış değerini daima sabit kaldığı bir fonksiyondur. Örneğin; $y(x)=4$ , bir sabit fonksiyondur. Çünkü, $x$ giriş değeri ne olursa olsun $y(x)$ değeri daima 4'tür (şekle bakın).

Temel özellikler

Sabit bir fonksiyonun genel denklemi; $y(x)=c$ veya yalnızca $y=c$ 'dir.

Örnek:

y(x)=2

veya yalnızca

y=2

fonksiyonu, çıkış değeri:

c=2

olan bir özel sabit fonksiyondur. Tanım kümesi, tüm ℝ reel sayılardır. Değer kümesi ise yalnızca {2}dir. Sabit fonksiyonun sağında x bağımsız değişkeni bulunmaz. y(0)=2, y(−2,7)=2, y(π)=2,.... Yani x giriş değeri ne olursa olsun, çıkış daima "2"dir.

Gerçek dünyadan örnek: Ne alırsan

1 olan bir mağaza.

$y=c$ sabit fonksiyonunun grafiği, düzlemde $(0,c)$ noktalarından geçen bir yatay doğrudur.

Matematiksel fonksiyonlar

Kümeler kuramına göre	Birebir fonksiyon Örten fonksiyon Birebir örten fonksiyon Birim fonksiyon Bileşke fonksiyon Sabit fonksiyon Boş fonksiyon Ters fonksiyon Özdeş fonksiyon Parçalı fonksiyon İçine fonksiyon

İşleme göre	Toplama fonksiyon Çarpma fonksiyon Çift fonksiyon Tek fonksiyon Alttoplamsal fonksiyon Üsttoplamsal fonksiyon

Topolojiye göre	Sürekli fonksiyon Hiçbir yerde sürekli fonksiyon Homeomorfizma

Sıralamaya göre	Monoton fonksiyon Sınırlı monoton fonksiyon

Gerçel/Karmaşık sayılara göre	Analitik fonksiyon Aritmetik fonksiyon Diferansiyellenebilir fonksiyon Düzgün fonksiyon Holomorf fonksiyon Meromorf fonksiyon Tam fonksiyon

This article is issued from Vikipedi - version of the 1/8/2017. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.