Tek ve çift fonksiyonlar

Matematikte, tek fonksiyon ve çift fonksiyon, aralarında simetri ilişki bulunan ve toplamaya göre tersleri olan fonksiyonlardır. Matematiksel analizin birçok alanında, özellikle kuvvet serisi ve Fourier serisinde sıkça kullanılır. Kuvvet fonksiyonunun eş kuvvetlerine göre adlandırılır ve şu şartı şağlar: Eğer n çift tam sayı ise, f(x) = xⁿ, çift fonksiyon; n tek tam sayı ise, fonksiyon tek fonksiyondur.

Tanım ve örnekler

Matematikte çiftlik ve teklik kavramları yalnızca, tanım ve değer kümelerinin her ikisinin de toplamaya göre tersleri olan fonksiyonlar için tanımlanır. Buna, abelian grup, tüm halkalar, tüm alanlar ve tüm vektör uzayları dahildir. Örneğin; bir reel değişkenin reel değerli fonksiyonu ve bir vektör değişkeninin karmaşık değerli fonksiyonu çift veya tek olabilir.

Çift fonksiyon

ƒ(x) = x², bir çift fonksiyondur.

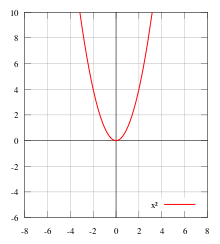
f(x), bir reel değişkenin reel değerli fonksiyonu olsun. Eğer aşağıdaki eşitlik, f tanım kümesindeki tüm x ve -x ler için sağlanıyorsa f, çifttir :

${\displaystyle f(x)=f(-x).\,}$

Geometriksel olarak ifade etmek gerekirse, bir çift fonksiyonun grafiği, y eksenine göre simetriktir. Yani y eksenine göre yansıtıldıktan sonra bile grafiği değişmez.

Çift fonksiyonlara örnek, |x|, x², x⁴, cos(x) ve cosh(x).

Tek fonksiyon

ƒ(x) = x³, bir tek fonksiyondur.

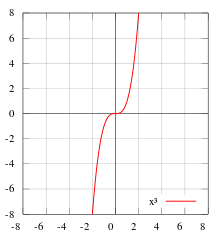
f(x), bir reel değişkenin reel değerli fonksiyonu olsun. Eğer aşağıdaki eşitlik, f tanım kümesindeki tüm x ve -x ler için sağlanıyorsa f, tektir :

${\displaystyle -f(x)=f(-x),\,}$

veya

${\displaystyle f(x)+f(-x)=0.\,}$

Geometriksel olarak ifade etmek gerekirse, bir tek fonksiyonun grafiği, orijine göre simetriktir Yani orijine göre 180 derece döndürüldükten sonra bile grafiği değişmez.

Tek fonksiyonlara örnek; x, x³, sin(x), sinh(x), ve erf(x).

Bazı durumları

Tek veya çift fonksiyon, sürekli olsa bile diferansiyellenebilir anlamına gelmez. Örneğin her yerde ayrık fonksiyon çifttir. Fakat hiçbir yerde sürekli değildir. Çiftlik durumu her iki alandada farklı incelenir.

Temel özellikler

• Tanım kümesi tüm reel sayılar için hem çift hem de tek olan fonksiyon sabit fonksiyondur ve aynı zamanda sıfırdır. (örneğin tüm x ler için, f(x) = 0).
• İki çift fonksiyonun toplamı çifttir. Bir çift fonksiyonun bir sabit ile çarpımı çifttir.
• İki tek fonksiyonun toplamı tektir . Bir tek fonksiyonun bir sabit ile çarpımı tektir.
• İki tek fonksiyonun farkı tektir.
• İki çift fonksiyonun farkı çifttir.
• İki çift fonksiyonun çarpımı çift fonksiyondur.
• İki tek fonksiyonun çarpımı çift fonksiyondur.
• Çift fonksiyon ile tek fonksiyonun çarpımı tek fonksiyondur.
• İki çift fonksiyonun bölümü çift fonksiyondur.
• İki tek fonksiyonun bölümü, çift fonksiyondur.
• Çift fonksiyon ile tek fonksiyonun bölümü tek fonksiyondur.
• Çift fonksiyonun türevi tektir.
• Tek fonksiyonun türevi çifttir.
• İki çift fonksiyonun bileşkesi çifttir.
• İki tek fonksiyonun bileşkesi tektir.
• Çift fonksiyon ile tek fonksiyonun bileşkesi çifttir.
• Ya tek ya da çift fonksiyon ile çift fonksiyonun bileşkesi çifttir (fakat tersi geçerli değildir).
• Tek fonksiyonunun, −A dan +A ya integrali sıfırdır. (burada A, sonludur ve fonksiyonun −A danA ya, dikey asimptotu yoktur).
• Çift fonksiyonun −A dan +A ya integrali, 0'dan +A ya iki kez integraline eşittir. (burada A, sonludur ve fonksiyonun −A dan A ya dikey asimptotu yoktur.) A sonsuz olduğunda, ancak ve ancak integral yakınsıyorsa bu doğrudur.

Tek ve çift fonksiyonların toplamı

• Her fonksiyon, çift ve tek fonksiyonu toplamı ile ifade edilebilir. İspat:

${\displaystyle f{(x)}}$, tüm reel sayılarda tanımlı herhangi bir fonksiyon olsun. Bunu, şöyle de sembolize edebiliriz:

${\displaystyle {\frac {f{(x)}}{2}}+{\frac {f{(x)}}{2}}+{\frac {f{(-x)}}{2}}-{\frac {f{(-x)}}{2}}}$.

Tekrar şöyle yazılabilir: ${\displaystyle {\frac {f{(x)}+f{(-x)}}{2}}+{\frac {f{(x)}-f{(-x)}}{2}}}$.

${\displaystyle g{(x)}}$, ${\displaystyle {\frac {f{(x)}+f{(-x)}}{2}}}$ ve ${\displaystyle h{(x)}}$, ${\displaystyle {\frac {f{(x)}-f{(-x)}}{2}}}$ olsun.

Burada, şu eşitlik elde edilir: ${\displaystyle f{(x)}=g{(x)}+h{(x)}}$.

Şimdi, ${\displaystyle g{(x)}}$, çifttir. ${\displaystyle \because g{(-x)}={\frac {f{(-x)}+f{(x)}}{2}}=g{(x)}}$.

${\displaystyle h{(x)}}$, tektir. ${\displaystyle \because h{(-x)}={\frac {f{(-x)}-f{(x)}}{2}}=-{\frac {f{(x)}-f{(-x)}}{2}}=-h{(x)}}$. Q.E.D.

• Çift ile tek fonksiyonun toplamı, fonksiyonlardan biri tanım kümesi üzerinde verilen sıfıra eşit olmadığı müddetçe, ne çifttir ne de tektir.

Seriler

• Çift fonksiyonun Maclaurin serisinde yalnızca çift kuvvetler bulunur.
• Tek fonksiyonun Maclaurin serisinde yalnızca tek kuvvetler bulunur.
• Periyodik çift fonksiyonun Fourier serisinde yalnızca kosinüs terimi bulunur.
• Periyodik tek fonksiyonun Fourier serisinde yalnızca sinüs terimi bulunur.

Cebirsel yapı

• Çift fonksiyonun herhangi bir doğrusal kombinasyonu çifttir ve çift fonksiyonlar reel sayılar üzerindeki vektör uzayında bulunur. Benzer şekilde tek fonksiyonun herhangi bir doğrusal kombinasyonu tektir ve tek fonksiyonlar da reel sayılar üzerinde vektör uzayında bulunur. Tüm reel değerli fonksiyonların vektör uzayı, tek ve çift fonksiyonların alt uzaylarının doğrudan toplamıdır. Başka bir ifade ile her f(x) fonksiyonu, çift fonksiyon ve tek fonksiyonun toplamı olarak eşsiz biçinde yazılabilir:

${\displaystyle f(x)=f_{\text{e}}(x)+f_{\text{o}}(x)\,,}$

burada

${\displaystyle f_{\text{e}}(x)={\tfrac {1}{2}}[f(x)+f(-x)]}$

çifttir ve

${\displaystyle f_{\text{o}}(x)={\tfrac {1}{2}}[f(x)-f(-x)]}$

tektir. Örneğin; eğer f üstel ise, f_e, cosh vef_o  sinh olur.

Ayrıca bakınız

• Taylor serisi
• Fourier serisi
• Kuvvet serisi
• Kuvvet fonksiyonu