Pisagor teoremi
| Geometri |
|---|

{{{altyazu}}} |
| Geometrinin tarihi |
|
Dalları
Öklidci geometri · Öklid dışı geometri · Analitik geometri · Riemannian geometrisi · Diferansiyel geometri · Tasarı geometri · Cebirsel geometri
|
|
Araştırma alanları
|
|
Önemli kavramlar
Nokta · Doğru · Dik · Paralel · Doğru parçası · Düzlem · Uzunluk · Alan · Hacim · Köşe · Açı · Eşlik · Benzerlik · Çokgen · Üçgen · Yükseklik · Hipotenüs · Pisagor teoremi · Dörtgen · Yamuk · Uçurtma · Paralelkenar (Dikdörtgen, Eşkenar dörtgen, Kare) · Köşegen · Simetri · Eğri · Daire · Çap · Silindir · Küre · Piramit · Boyutlar (Bir, İki, Üç, Dört)
|
|
Geometriciler
Aryabhata · Ahmes · Apolonius · Archimedes · Baudhayana · Bolyai · Brahmagupta · Euclid · Pisagor · Khayyám · Descartes · Pascal · Euler · Gauss · Ibn al-Yasamin · Jyeṣṭhadeva · Kātyāyana · Lobachevsky · Manava · Minggatu · Riemann · Klein · Parameshvara · Poincaré · Sijzi · Hilbert · Minkowski · Cartan · Veblen · Sakabe Kōhan · Gromov · Atiyah · Virasena · Yang Hui · Yasuaki Aida · Zhang Heng
|

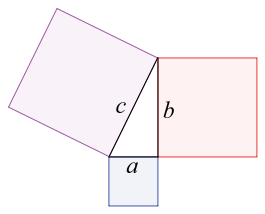
Pisagor (Pythagoras) isimli Yunan matematikçisi milattan önce 570 ile 475 yılları arasında yaşamıştır. Dik üçgenin kenar uzunlukları arasındaki ilişkiye ait çalışmalar yapmıştır. Çalışmalar sonunda elde ettiği sonuçlar da Pisagor bağıntısı olarak matematikte yerini almıştır. Pisagor bağıntısı bir dik üçgenin iki kenar uzunluğu verildiğinde üçüncü kenarın uzunluğunu bulmamızı sağlar Pisagor teoremine göre bir dik üçgende dik kenarın yani hipotenüsün bir kenarını oluşturduğu karenin alanı diğer iki dik kenarın birer kenar olarak oluşturdukları karelerin alanları toplamına eşittir:
c uzunluğu hipotenüstür. a ve b uzunlukları ise dik kenarlardır. Her kenardan birer kare oluşturulur. Bu karelerin alanları, kare alan formülüne dayalı olarak şeklinde sıralanır. Böylece üç karenin köşelerinin birleşiminden oluşan bir dik üçgen oluşturulur. Oluşan üçgenin dik köşesinden hipotenüsün oluşturduğu karenin, hipotenüse paralel olan kenara indirilen dikme ile üçgen içerisinde Öklid bağıntısı kurulur. (öklid bağıntısı benzerlikten ispatlanabilmektedir.) Öklide göre
yani, dik kenarlardan birinin karesi, dik açıdan hipotenüse indirilen dikmenin ayırdığı parçalardan kendisine komşu olan tarafın uzunluğu ile hipotenüsün tamamının çarpımına eşittir. Bu durumda
olacaktır. Yani a kenarına ait karenin alanı, hipotenüse ait alanın dik açıdan indirilen dikmeyle ikiye ayırdığı alanlardan kendisine komşu olan alana eşit olacaktır. Bu durumu diğer kenar için de düşünürüz.
olacaktır. Bunu takiben,
olacaktır.
Matematikte, Pisagor Teoremi, Öklid geometrisinde bir dik üçgenin 3 kenarı için bir bağıntıdır. Bilinen en eski matematiksel teoremlerden biridir. Teorem sonradan MÖ 6. yüzyılda Yunan filozof ve matematikçi Pisagor'a atfen isimlendirilmiş ise de, Hindu, Yunan, Çinli ve Babilli matematikçiler teoremin unsurlarını, o yaşamadan önce bilmekteydiler.
Pisagor teoreminin bilinen ilk ispatı Öklid'in Elementler eserinde bulunabilir....
Sayısal Örnekler
En yaygın olarak karşılaşılan örneklerden biri "3-4-5" üçgenidir.
Bu, komşu kenarları sırasıyla 3 birim, 4 birim ve karşı kenarı 5 birim olan bir dik üçgeni temsil eder.
Diğer örnekleri ise ...
Pisagor teoremi bir dik açı oluşturmak kolaydır.
Şöyle ki:
1) Yeterli uzunlukta bir halatı(ya da ipliği) eşit 12 parçaya ayıracak şekilde işaretleyin.
2) Bu işaretlerden 3. ve 5. (3+5) noktalari sabitleyip, ipin açıkta kalan iki ucunu (gergin olacak şekilde) birleştirin.
3) 3. işaretin bulunduğu noktada bir dik açı elde edersiniz.
Bu yöntemin geçmişte tarım alanlarının paylaşılması, arazi sınırlarının belirlenmesi gibi alanlarda kullanıldığı bilinmektedir...
| ||||||||||||||||