Heisenberg cebiri

Matematik'te, Heisenberg grubu,Werner Heisenberg adına ithaf edilmiştir,3×3 formun üst üçgen matrisler'inin grubu'dur

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}}$

veya matris çarpımının operasyonu altında bir genelleştirmedir. Ögelerden a, b ve c, bazıları (keyfi) değişmeli halka ile özdeş alınmaktadır, sıklıkla gerçel sayılar halkası veya tamsayı'lar halkası alınmaktadır. Gerçek Heisenberg grubu tek-boyutlu kuantum mekanik sistemlerin tanımı içinde ortaya çıkar. daha genel olarak, bir n-boyutlu sistemlerle ilişkili gruplar olarak dikkate alınabilir, ve yine daha genel olarak,herhangi simplektik vektör uzayı'nda.

Üç boyutlu durum

üç boyutlu durum içinde,iki Heisenberg matrisin çarpımı ile:

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}{\begin{pmatrix}1&a'&c'\\0&1&b'\\0&0&1\\\end{pmatrix}}={\begin{pmatrix}1&a+a'&c+c'+ab'\\0&1&b+b'\\0&0&1\\\end{pmatrix}}\,.}$

Buradakiler üç boyutlu durumun birkaç sayıda önde gelen örnekleridir.

Sürekli Heisenberg grubu

Eğer a, b, c, gerçel sayılar (R halkası içinde) idiyse bir sürekli Heisenberg grubu H₃(R) dir.

Bu bir nilpotent Lie grubudur.

Buna ek olarak gerçek 3x3 matrislerin gösterimi,sürekli Heisenberg grubu gibi birçok farklı gösterimler fonksiyon uzay'larınin terimleri içinde idi.Stone–von Neumann teoremi tarafından,belirli bir sıradan olmayan karakter tarafındanmerkez hareketi içinde H'in bir bütün olarak indirgenemeyen bölünmez gösterimidir.Bu gösterim birkaç önemli gerçekleştirme veya modelleri Schrödinger model i içinde,Heisenberg grup hareketi İntegrallenebilir kare fonksiyon'larının uzayı olarak teta gösterim içinde idi bu üstyarı-düzlemde holomorfik fonksiyonların uzayın hareketidir ; Bu nedenle adı teta fonksiyon'ları ile bağlantıdır.

Ayrık Heisenberg grubu

Ayrık Heisenberg grubunun Cayley grafı'nın bir parçası , konu içinde x,y,z üreteçleri olarak. (renklendirme sadece görsellik içindir)

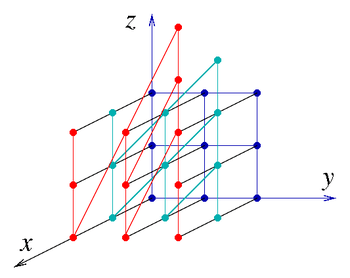
Eğer a, b, c,tamsayılar (Z halkası içinde) ise bir ayrık Heisenberg grubu H₃(Z) idi.Bu bir değişmeli-olmayan nilpotent grup'tur. Bu iki üreteç idi,

${\displaystyle x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}}$

ve ilişkiler

${\displaystyle z_{}^{}=xyx^{-1}y^{-1},\ xz=zx,\ yz=zy}$,

burada

${\displaystyle z={\begin{pmatrix}1&0&1\\0&1&0\\0&0&1\\\end{pmatrix}}}$

H₃'ün merkez'inin generatörüdür . (Unutmadan x, y, ve znin tersi için 1 yerine yukarıda köşegene −1 konulur.) Unutmayın tersleri x, y, ve z -1 ile çapraz yukarıdaki 1 değiştirin.) Bass's teoremi ile, bu sıra 4 ün bir polinom büyüme kesri idi.

Herhangi bir öge aracılığı ile üretilebilir

${\displaystyle {\begin{pmatrix}1&a&c\\0&1&b\\0&0&1\\\end{pmatrix}}=y^{b}z^{c}x^{a}\,.}$

Heisenberg grup modül p tek asalı

Eğer bir Z/p içinde a, b, c alınırsa Z için bir tek asal p,ise bir Heisenberg grup modül p idi. Bu bir dizi grubu p³ ile üreteçler x,y ve ilişkilidir:

${\displaystyle z_{}^{}=xyx^{-1}y^{-1},\ x^{p}=y^{p}=z^{p}=1,\ xz=zx,\ yz=zy.}$

Tek asal düzenin p sonlu cisimler üzerinde tanımlı Heisenberg grupların analogları ekstra özel grup olarak adlandırılır ,ya da daha çok uygun bir şekilde,p üs'sün ekstra özel grubudur. daha genel olarak, Eğer bir grup G türev altgrupları G' nin merkezinde yer alan Z ise G/Z × G/Z → Z haritasında bir çarpık-simetrik çiftdoğrusal operatör olarak değişmeli gruplardır.Ancak, G/Znin bir sonlu vektör uzayı olması için gereken G nin Frattini altgrubu merkezinde yer alacaksa, ve Z üzerinde bir tek boyutlu vektör uzayı üzerinde Z/p Z Zye gereken p düzeni vardır, Eğer öğleyse Gdeğişmeli değil, ise G ektra özeldir. Eğer G ektra özel ama üs p yok, ise simplektik vektör alanı G/Zye uygulanan aşağıdaki genel yapı Giçin izomorfik bir grup ortaya koymamıştır.

Heisenberg grup modül 2

8'in yerine Heisenberg grup modül 2'dir ve izomorfik iki-düzlemli grup(v şeklinde) D₄ tir(bir karenin simetrisi). Eğer gözlemlenir

${\displaystyle x={\begin{pmatrix}1&1&0\\0&1&0\\0&0&1\\\end{pmatrix}},\ \ y={\begin{pmatrix}1&0&0\\0&1&1\\0&0&1\\\end{pmatrix}}}$.

ise

${\displaystyle xy={\begin{pmatrix}1&1&1\\0&1&1\\0&0&1\\\end{pmatrix}},}$

ve

${\displaystyle yx={\begin{pmatrix}1&1&0\\0&1&1\\0&0&1\\\end{pmatrix}}.}$

Bu ögeler x ve y yansımaya karşılıktır (45°ara ile), oysa xy veyx 90° rotasyona karşılık. Diğer yansıma xyx ve yxydir, ve 180°dönme ilexyxy (=yxyx)dir.

Yüksek boyutlar

Daha genel Heisenberg grupları H_n Öklid uzayının yüksek boyutlarda,ve daha genel olarak üzerinde basitlestirilmis vektör uzayı tanımlanabilir.En basit genel durum herhangi bir tamsayı n ≥ 1 için 2n+1 boyutlu gerçel Heisenberg grubunun durumudur.Matrislerin bir grup olarak, H_n (veya H_n(R) Bu halka üzerinde Heisenberg grubunu belirtmek içinR veya gerçel sayılar) n+2 boyutlu R içine girdiler ile kare matrislerin grubu olarak tanımlanır :

${\displaystyle {\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}}$

burada

a n uzunluğunun bir satır vektör'üdür,

b n uzunluğunun bir sütun vektör'üdür,

I_n nin boyut birim matris'tir.

Grup Yapısı

Çarpma ile gösterildiği gibi bu, gerçekten de bir gruptur:

${\displaystyle {\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&\mathbf {a} '&c'\\0&I_{n}&\mathbf {b} '\\0&0&1\end{bmatrix}}={\begin{bmatrix}1&\mathbf {a} +\mathbf {a} '&c+c'+\mathbf {a} \cdot \mathbf {b} '\\0&I_{n}&\mathbf {b} +\mathbf {b} '\\0&0&1\end{bmatrix}}}$

ve

${\displaystyle {\begin{bmatrix}1&\mathbf {a} &c\\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}\cdot {\begin{bmatrix}1&-\mathbf {a} &-c+\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&-\mathbf {b} \\0&0&1\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&I_{n}&0\\0&0&1\end{bmatrix}}.}$

Heisenberg grubu bir Lie cebiri Lie grubunun bağlantılı, basit-bağlantılı matrislerinden oluşmaktadır.

${\displaystyle {\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}},}$

burada

a n uzunluğunda bir satır vektördür,

b n uzunluğunda bir sütun vektörüdür,

0_n nin boyutu sıfır matristir.

Üstel Harita

üstel harita ile verilen aşağıdaki bağıntılar

${\displaystyle \exp {\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}}=\sum _{k=0}^{\infty }{\frac {1}{k!}}{\begin{bmatrix}0&\mathbf {a} &c\\0&0_{n}&\mathbf {b} \\0&0&0\end{bmatrix}}^{k}={\begin{bmatrix}1&\mathbf {a} &c+{1 \over 2}\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&\mathbf {b} \\0&0&1\end{bmatrix}}.}$

e₁, ..., e_n yardımıyla Rⁿ kuralli tabanıdır,ve çerçeve

${\displaystyle p_{i}={\begin{bmatrix}0&\operatorname {e} _{i}^{\mathrm {T} }&0\\0&0_{n}&0\\0&0&0\end{bmatrix}},}$

${\displaystyle q_{j}={\begin{bmatrix}0&0&0\\0&0_{n}&\operatorname {e} _{j}\\0&0&0\end{bmatrix}},}$

${\displaystyle z={\begin{bmatrix}0&0&1\\0&0_{n}&0\\0&0&0\end{bmatrix}},}$

Bu ilişkisel Lie cebiri kuralli degisim ilişkileri tarafından karakterize edilebilir,

${\displaystyle {\begin{bmatrix}p_{i},q_{j}\end{bmatrix}}=\delta _{ij}z,\qquad \qquad {\begin{bmatrix}p_{i},z\end{bmatrix}}=0,\qquad {\begin{bmatrix}q_{j},z\end{bmatrix}}=0~,}$

burada p₁, ..., p_n, q₁, ..., q_n, z cebir üretecidir.

özel olarak, z Heisenberg Lie cebirinin bir merkez ögesidir. Unutmadan Heisenberg grubunun nilpotenti Lie cebridir Bir nilpotent Lie cebrinin üstel haritası bir difeomorfizm ile Lie cebiri arasında ve birimsel ilişkili bağlantılı, basit-bağlantılı Lie grubudur.

Bu konuda (boyut ve Lie grubuna atıfta bulunarak) eğer herhangi değişmeli halka A yı R yerine uygularsak,buna tekabül eden grup H_n(A ) ifadesidir. Asal 2 Ek varsayımlar altında A halkasının içinde terside olabilir,üstel harita ayrıca tanımlanmıştır,bundan dolayı bir sonlu toplamı ve yukarıdaki formu azaltır.(ör. A bir halka olabilir Z/p Z ile bir tek asal p veya herhangi karakteristik 0'ın alanı).

Ayrıca bakınız

• Weyl parçalaması
• Stone–von Neumann teoremi

Kaynakça

• Ernst Binz & Sonja Pods (2008). Geometry of Heisenberg Groups. Amerikan Matematik Derneği. ISBN 978-0-8218-4495-3. 
• Hall, Brian C. (2004). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Berlin: Springer. ISBN 0-387-40122-9. 
• Roger Evans How (1980). "On the role of the Heisenberg group in harmonic analysis". 
• Kirilov, A.A. (2004). Lectures on the Orbit Method, Chapter 2: "Representations and Orbits of the Heisenberg Group",. American Mathematical Society. ISBN 0-8218-3530-0. 
• G. Mackey (1976). The theory of Unitary Group Representations (Chicago Lectures in Mathematics). University Of Chicago Press. ISBN 978-0226500522. 

Dış bağlantılar

• Groupprops, The Group Properties Wiki Unitriangular matrix group UT(3,p)