Hiperbolik fonksiyon

Orijinden geçen bir ışın ${\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}$ hiperbolünü ${\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}$ noktasında keser ve ${\displaystyle \scriptstyle a}$ ışın ile ${\displaystyle \scriptstyle x}$-ekseni arasındaki alanın iki katıdır. Hiperbolün üzerinde ${\displaystyle \scriptstyle x}$-ekseninin altında kalan noktalar için alan negatif sayılır.(Trigonometrik fonksiyonlar ile karşılaştırmak için bakınız.

Matematikte, hiperbolik fonksiyonlar sıradan trigonometrik fonksiyonların analogudur. Temel hiperbolik fonksiyonlar hiperbolik sinüs "sinh", hiperbolik kosinüs "cosh", bunlardan türetilen hiperbolik tanjant "tanh" ^[1] ve benzer fonksiyonlardır. Ters hiperbolik fonksiyonlar alan hiperbolik sinüsü "arsinh" ("asinh" ya da "arcsinh" olarak da gösterilir)^[2] ve benzeri fonksiyonlardır.

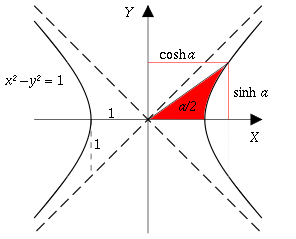
(cos t, sin t) noktalarının birim yarıçaplı bir çember oluşturması gibi, (cosh t, sinh t) noktaları da eşkenar hiperbolün sağ yarısını oluşturur. Hiperbolik fonksiyonlar, zincir eğrisini tanımlayan denklem ile elekromanyetik teori, ısı transferi, akışkanlar dinamiği ve özel görelilik gibi fiziğin çeşitli alanlarında önemli bir denklem olan Kartezyen koordinat sisteminde Laplace denklemi gibi lineer diferansiyel denklemlerin çözümlerinde görülür.

Hiperbolik açı adı verilen gerçek bağımsız değişkenler için hiperbolik fonksiyonların değeri de gerçektir. Karmaşık analizde ise basitçe üstel fonksiyonların rasyonel fonksiyonlarıdır, dolayısıyla meromorf fonksiyonlardır.

Hiperbolik fonksiyonlar, 1760'larda birbirlerinden bağımsız olarak Vincenzo Riccati ve Johann Heinrich Lambert tarafından tanımlanmıştır.^[3] Riccati dairesel fonksiyonlar için Sc. ve Cc. ([co]sinus circulare) hiperbolik fonksiyonlar için ise Sh. ve Ch. ([co]sinus hyperbolico) kısaltmalarını kullanmıştır. Lambert aynı isimleri kullanmış ancak kısaltma olarak günümüzde kullanılan kısaltmaları kullanmıştır.^[4] sh ve ch kısaltmaları Fransızca ve Rusça gibi bazı dillerde günümüzde de kullanılmaktadır.

Standart cebirsel denklikler

sinh, cosh ve tanh

csch, sech ve coth

(a) cosh(x) e^x ve e^−x fonksiyonlarının ortalamasıdır

(b) sinh(x) e^x ile e^−x fonksiyonlarının farkının yarısıdır

(a) cosh ve (b) sinh hiperbolik fonksiyonları ${\displaystyle e^{x}}$ ve ${\displaystyle e^{-x}}$ üstel fonksiyonları kullanılarak elde edilmiştir

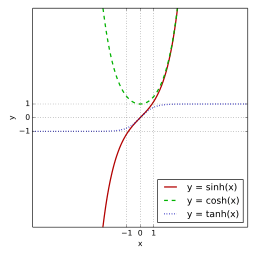
Hiperbolik fonksiyonlar şunlardır:

• Hiperbolik sinüs:

${\displaystyle \sin x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}}$

• Hiperbolik kosinüs:

${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}}$

• Hiperbolik tanjant:

${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}$

• Hiperbolik kotanjant:

${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}$

• Hiperbolik sekant:

${\displaystyle \operatorname {sech} \,x=\left(\cosh x\right)^{-1}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}$

• Hiperbolik kosekant:

${\displaystyle \operatorname {csch} \,x=\left(\sinh x\right)^{-1}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}$

Hiperbolik fonksiyonlar karmaşık düzlemde dairesel açılarla da ifade edilebilir:

• Hiperbolik sinüs:

${\displaystyle \sinh x=-{\rm {i}}\sin {\rm {i}}x\!}$

• Hiperbolik kosinüs:

${\displaystyle \cosh x=\cos {\rm {i}}x\!}$

• Hiperbolik tanjant:

${\displaystyle \tanh x=-{\rm {i}}\tan {\rm {i}}x\!}$

• Hiperbolik kotanjant:

${\displaystyle \coth x={\rm {i}}\cot {\rm {i}}x\!}$

• Hiperbolik sekant:

${\displaystyle \operatorname {sech} \,x=\sec {{\rm {i}}x}\!}$

• Hiperbolik kosekant:

${\displaystyle \operatorname {csch} \,x={\rm {i}}\,\csc \,{\rm {i}}x\!}$

i, i² = −1 olarak tanımlanan sanal birimdir.

Yukarıdaki denkliklerin karmaşık sayı biçimleri Euler denkleminden gelir.

Kabul edilen konvansiyon gereği, sinh² x, (sinh x)² anlamına gelir ve sinh(sinh x) demek değildir. Bu kabul pozitif üstler ile diğer hiperbolik fonksiyonlar için de geçerlidir. Hiperbolik kotanjant fonksiyonu ctnh x olarak da yazılır ama coth x gösterimi daha yaygındır.

Yararlı bağıntılar

${\displaystyle \sinh(-x)=-\sinh x\,\!}$

${\displaystyle \cosh(-x)=\cosh x\,\!}$

Dolayısıyla:

${\displaystyle \tanh(-x)=-\tanh x\,\!}$

${\displaystyle \coth(-x)=-\coth x\,\!}$

${\displaystyle \operatorname {sech} (-x)=\operatorname {sech} \,x\,\!}$

${\displaystyle \operatorname {csch} (-x)=-\operatorname {csch} \,x\,\!}$

cosh x ve sech x çift fonksiyon, diğerleri tek fonksiyondur.

${\displaystyle \operatorname {arsech} \,x=\operatorname {arcosh} {\frac {1}{x}}}$

${\displaystyle \operatorname {arcsch} \,x=\operatorname {arsinh} {\frac {1}{x}}}$

${\displaystyle \operatorname {arcoth} \,x=\operatorname {artanh} {\frac {1}{x}}}$

Hiperbolik sinüs ve kosinüs, Pisagor trigonometrik özdeşliği'ne benzeyen aşağıdaki özdeşliği sağlar

${\displaystyle \cosh ^{2}x-\sinh ^{2}x=1\,}$

Diğer fonksiyonlar için de şu özdeşlikler sağlanır

${\displaystyle \tanh ^{2}x=1-\operatorname {sech} ^{2}x}$

${\displaystyle \coth ^{2}x=1+\operatorname {csch} ^{2}x}$

Hiperbolik tanjant nonlineer sınır değeri probleminin çözümüdür^[5]:

${\displaystyle {\frac {1}{2}}f''=f^{3}-f\qquad ;\qquad f(0)=f'(\infty )=0}$

cosh x eğrisinin altındaki alanın her zaman yay uzunluğuna eşit olduğu gösterilebilir:^[6]

${\displaystyle {\text{alan}}=\int _{a}^{b}{\cosh {x}}\ dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh {x}\right)^{2}}}\ dx={\text{yay uzunluğu}}.}$

Logaritma olarak ters fonksiyonlar

${\displaystyle \operatorname {arsinh} \,x=\ln \left(x+{\sqrt {x^{2}+1}}\right)}$

${\displaystyle \operatorname {arcosh} \,x=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1}$

${\displaystyle \operatorname {artanh} \,x={\tfrac {1}{2}}\ln {\frac {1+x}{1-x}};\left|x\right|<1}$

${\displaystyle \operatorname {arcoth} \,x={\tfrac {1}{2}}\ln {\frac {x+1}{x-1}};\left|x\right|>1}$

${\displaystyle \operatorname {arsech} \,x=\ln {\frac {1+{\sqrt {1-x^{2}}}}{x}};0<x\leq 1}$

${\displaystyle \operatorname {arcsch} \,x=\ln \left({\frac {1}{x}}+{\frac {\sqrt {1+x^{2}}}{\left|x\right|}}\right)}$

Türevler

${\displaystyle {\frac {d}{dx}}\sinh x=\cosh x\,}$

Ayrıştırılamadı (bilinmeyen işlev "\sih"): {\displaystyle \frac{d}{dx}\cosh x = \sih x \,}

${\displaystyle {\frac {d}{dx}}\tanh x=1-\tanh ^{2}x={\hbox{sech}}^{2}x=1/\cosh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\coth x=1-\coth ^{2}x=-{\hbox{csch}}^{2}x=-1/\sinh ^{2}x\,}$

${\displaystyle {\frac {d}{dx}}\ {\hbox{csch}}\,x=-\coth x\ {\hbox{csch}}\,x\,}$

${\displaystyle {\frac {d}{dx}}\ {\hbox{sech}}\,x=-\tanh x\ {\hbox{sech}}\,x\,}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{\left|x\right|{\sqrt {1+x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}$

${\displaystyle {\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}}$

Standart İntegraller

${\displaystyle \int \sinh ax\,dx=a^{-1}\cosh ax+C}$

${\displaystyle \int \cosh ax\,dx=a^{-1}\sinh ax+C}$

${\displaystyle \int \tanh ax\,dx=a^{-1}\ln(\cosh ax)+C}$

${\displaystyle \int \coth ax\,dx=a^{-1}\ln(\sinh ax)+C}$

${\displaystyle \int {\frac {du}{\sqrt {a^{2}+u^{2}}}}=\sinh ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{\sqrt {u^{2}-a^{2}}}}=\cosh ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\tanh ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}<a^{2}}$

${\displaystyle \int {\frac {du}{a^{2}-u^{2}}}=a^{-1}\coth ^{-1}\left({\frac {u}{a}}\right)+C;u^{2}>a^{2}}$

${\displaystyle \int {\frac {du}{u{\sqrt {a^{2}-u^{2}}}}}=-a^{-1}\operatorname {sech} ^{-1}\left({\frac {u}{a}}\right)+C}$

${\displaystyle \int {\frac {du}{u{\sqrt {a^{2}+u^{2}}}}}=-a^{-1}\operatorname {csch} ^{-1}\left|{\frac {u}{a}}\right|+C}$

C sabit sayıdır.

Taylor dizisi gösterimi

Yukarıdaki fonksiyonları Taylor dizisi olarak da göstermek mümkündür:

${\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}$

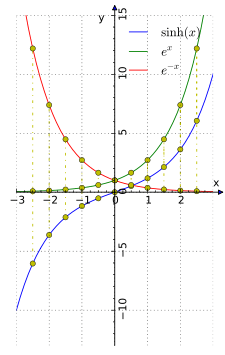
sinh x fonksiyonunun Taylor dizisi gösteriminde x için yalnızca tek üstel bileşenler bulunur. Tek fonksiyon olduğundan ötürü −sinh x = sinh(−x) ve sinh 0 = 0 doğrudur.

${\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}$

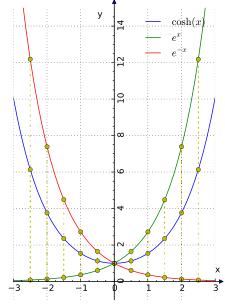
cosh x fonksiyonunun Taylor dizisi gösteriminde x için yalnızca çift üstel bileşenler bulunur. Dolayısıyla çift fonksiyondur yani y-eksenine göre simetriktir. sinh ve cosh dizilerinin toplamı üstel fonksiyonun sonsuz dizi gösterimidir.

${\displaystyle \tanh x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \coth x=x^{-1}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$ (Laurent dizisi)

${\displaystyle \operatorname {sech} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}$

${\displaystyle \operatorname {csch} \,x=x^{-1}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }$ (Laurent dizisi)

${\displaystyle B_{n}\,}$ ninci Bernoulli sayısıdır

${\displaystyle E_{n}\,}$ ninci Euler sayısıdır

Dairesel trigonometrik fonksiyonlarla karşılaştırma

Kartezyen düzlemin aşağıdaki iki altkümesi ele alındığında

${\displaystyle A=\lbrace (\cosh t,\sinh t):t\in R\rbrace \quad {\text{ve}}\quad B=\lbrace (\cos t,\sin t):t\in R\rbrace .}$

A birim hiperbolün sağ dalını oluşturur iken {(x,y): x² − y² = 1}, B birim çemberi oluşturur. Doğal olarak ${\displaystyle A\cap B}$ = {(1,0)} dır. Aradaki temel fark t → B periyodik fonksiyon iken t → A değildir.

Hiperbolik fonksiyonlar trigonometrik özdeşliklere biçimsel olarak benzeyen birçok özdeşliği sağlar. Aslında, Osborn kuralı^[7] herhangi bir trigonometrik özdeşliğin, sinüs ve kosinüslerin üstlerinin integrali olarak genişletildiğinde, sinüsün sinh'a, kosinisün cosh'a değiştirilmesi ve 2, 6, 10, 14, ... sinh çarpımı içeren tüm terimlerin işaretinin değiştirilmesiyle hiperbolik özdeşlikler elde edileceğini gösterir. Örneğin toplama teoremleri:

${\displaystyle \sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y\,}$

${\displaystyle \cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y\,}$

${\displaystyle \tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\,}$

"çift değişken formülleri"

${\displaystyle \sinh 2x\ =2\sinh x\cosh x\,}$

${\displaystyle \cosh 2x\ =\cosh ^{2}x+\sinh ^{2}x=2\cosh ^{2}x-1=2\sinh ^{2}x+1\,}$

${\displaystyle \tanh 2x\ ={\frac {2\tanh x}{1+\tanh ^{2}x}}\,}$

ve "yarım değişken formülleri"^[8]

${\displaystyle \sinh {\tfrac {x}{2}}={\sqrt {{\tfrac {1}{2}}(\cosh x-1)}}\,}$    Not: Dairesel karşılığının −1 ile çarpılmışına denktir.

${\displaystyle \cosh {\tfrac {x}{2}}={\sqrt {{\tfrac {1}{2}}(\cosh x+1)}}\,}$    Not: Dairesel karşılığına denktir..

sinh x 'in türevi cosh x ve cosh x 'in türevi sinh x 'tır. Bu dairesel fonksiyonlara benzer ancak işareti farklıdır (örneğin, cos x 'in türevi −sin x 'tir).

Gudermannian fonksiyonu karmaşık sayıları içermeyen hiperbolik fonksiyonlar ile dairesel fonksiyonlar arasında doğrudan bağıntıları verir.

a cosh(x/a) fonksiyonunun grafiği zincir eğrisi, yani uniform esnek bir zincirin iki sabit noktadan asıldığında uniform yerçekimi kuvveti etkisiyle oluşturduğu eğridir.

Üstel fonksiyon ile olan bağlantı

Hiperbolik sinüs ve kosinüs tanımlarından aşağıdaki özdeşlikleri çekebiliriz:

${\displaystyle e^{x}=\cosh x+\sinh x\!}$

ve

${\displaystyle e^{-x}=\cosh x-\sinh x.\!}$

Bu gösterimler, karmaşık üstel fonksiyonların toplamı olarak, Euler denklemine göre sinüs ve kosinüs gösterimlerine benzerdir.

Karmaşık sayılar için hiperbolik fonksiyonlar

Herhangi bir karmaşık değişken için üstel fonksiyon tanımlanabildiği için hiperbolik fonksiyonların tanımları karmaşık değişkenlere de uygulanabilir. Dolayısıyla sinh z ve cosh z fonksiyonları holomorf fonksiyondur.

Karmaşık sayılar için trigonometrik fonksiyonlar Euler denklemi ile verilir:

${\displaystyle e^{ix}=\cos x+i\;\sin x}$

${\displaystyle e^{-ix}=\cos x-i\;\sin x}$

dolayısıyla:

${\displaystyle \cosh ix={\tfrac {1}{2}}(e^{ix}+e^{-ix})=\cos x}$

${\displaystyle \sinh ix={\tfrac {1}{2}}(e^{ix}-e^{-ix})=i\sin x}$

${\displaystyle \cosh(x+iy)=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\,}$

${\displaystyle \sinh(x+iy)=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\,}$

${\displaystyle \tanh ix=i\tan x\,}$

${\displaystyle \cosh x=\cos ix\,}$

${\displaystyle \sinh x=-i\sin ix\,}$

${\displaystyle \tanh x=-i\tan ix\,}$

Dolayısıyla hiperbolik fonksiyonlar ${\displaystyle 2\pi i}$ (hiperbolik tanjant ve kotanjant için ${\displaystyle \pi i}$) periyoduyla imajiner bileşen için periyodiktir.

Karmaşık düzlemde hiperbolik fonksiyonlar

${\displaystyle \operatorname {sinh} (z)}$	${\displaystyle \operatorname {cosh} (z)}$	${\displaystyle \operatorname {tanh} (z)}$	${\displaystyle \operatorname {coth} (z)}$	${\displaystyle \operatorname {sech} (z)}$	${\displaystyle \operatorname {csch} (z)}$

Ayrıca bakınız

• Matematiksel fonksiyonların listesi

Notlar

1. tanh
2. Some examples of using arcsinh. Google Books'ta bulunan örnekler.
3. Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America, 2007. Page 100.
4. Georg F. Becker. Hyperbolic functions. Read Books, 1931. Page xlviii.
5. Eric W. Weisstein. "Hyperbolic Tangent". MathWorld. 11 Eylül 2015 tarihinde kaynağından arşivlendi. http://web.archive.org/web/20150911113850/http://mathworld.wolfram.com/HyperbolicTangent.html. Erişim tarihi: 2008-10-20. 
6. N.P., Bali (2005). Golden Intergral Calculus. Firewall Media. s. 472. ISBN 8-170-08169-6. http://books.google.com/books?id=hfi2bn2Ly4cC. , Extract of page 472
7. G. Osborn, Mnemonic for hyperbolic formulae, The Mathematical Gazette, p. 189, volume 2, issue 34, July 1902
8. Peterson, John Charles (2003). Technical mathematics with calculus (3rd bas.). Cengage Learning. s. 1155. ISBN 0-766-86189-9. http://books.google.com/books?id=PGuSDjHvircC. , Chapter 26, page 1155

Dış bağlantılar

• Hiperbolik fonksiyonlar PlanetMath
• Hiperbolik fonksiyonlar MathWorld
• GonioLab: Birim çember, trigonometrik ve hiperbolik fonksiyonların gösterimi (Java Web Start)
• Web-tabanlı hiperbolik fonksiyon hesap makinesi